ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
НАКЛЕП
Деформационное упрочнение связано с размножением дислокаций и увеличением их плотности при работе источников дислокаций. При этом возникают дополнительные усилия, связанные с двумя факторами. Во-первых, появляются новые точки закрепле-
ния дислокаций, и уменьшается расстояние L между точками закрепления у их источников. Критическое напряжение открытия источников по формуле (4.28) возрастает. Во-вторых, возрастает число точек пересечения движущейся дислокации с расположенными в других плоскостях дислокациями («лесом» дислокаций). При пересечении двух дислокаций образуются либо ступеньки, либо вакансии. Их образование требует расхода энергии. Поэтому с увеличением плотности «леса» дислокаций возрастает сопротивление металла пластической деформации.
Вероятно, ведущую роль играет блокирующее взаимодействие полей напряжений соседних дислокаций. Максимальное напряжение, необходимое для преодоления этого взаимодействия, можно получить из формулы (4.25):
|
G • b cos(0) • cos(20) |
G • b = G • b •'/p 2n(1 — v) L 2n-(1 — v),
2я-г (1 — v)
где L = 1/ p1/2 — среднее расстояние между дислокациями, р — их плотность.
Угол сдвига у связан с длиной среднего пробега дислокаций X и плотностью дислокаций формулой у = р'1-b. Если, как в a-Fe, длина свободного пробега X практически постоянна, то ф/5у = 1/ (X ' b) = const. Дифференцируя предыдущую формулу, получим:
дт_ G - b д^_ G - b
дУ 2л-(1 -v) дУ л п fa (5.36)
4л-(1 - v) - у
Можно предположить, что упрочнение при наклепе будет обратно пропорционально среднему расстоянию между дислокациями, а угол наклона кривой нагружения (касательный модуль) с ростом деформации будет изменяться обратно пропорционально корню квадратному из интенсивности наклепа 1/^/у.
При пересечении двух винтовых дислокаций за местом пересечения тянется хвост диполей, или хвост вакансий. На образование каждой вакансии нужно затратить определенную энергию. Следовательно, связанная с этим процессом часть сопротивления движению дислокаций должна быть обратно пропорциональна расстоянию между пересекаемыми дислокациями:
Ї-Я-Ui. '5-37>
В случаях пересечения краевых дислокаций на подвижной дислокации после пересечения образуется ступенька, равная вектору
Бюргерса неподвижной дислокации. При этом, согласно формуле (4.19) или (4.20), на образование каждой ступеньки нужно затратить энергию, примерно равную
|
|
(5.38)
Как и в предыдущем случае, приращение сопротивления движению дислокации от этого механизма должно быть обратно пропорциональным расстоянию между ступеньками L = р-1/2, а касательный модуль упрочнения должен быть пропорционален правой части формулы (5.37).
Таким образом, все рассмотренные механизмы упрочнения, связанные с наклепом, приводят к зависимостям вида
doj_ = A
dei &
либо
|
|
где стг, ег — интенсивность напряжений и интенсивность пластических деформаций; А — постоянная для заданной кривой нагружения.
|
(5.39) |
Кривую нагружения можно получить интегрированием этих формул. Она примет вид:
Ъ = Ъ0 + A ■ en,
где показатель упрочнения nдолжен быть в пределах 0,5...1,5. Но в действительности показатель упрочнения конструкционных сталей при ст0 = 0 обычно находится в пределах 0,1...0,2. Очевидно, в приведенных расчетах многое не учтено.
Дислокации образуют клубки. Далее формируется ячеистая структура, показанная на рис. 5.23.
Белые островки почти не содержат дислокаций. Их размеры примерно такие же, как размеры металлических усов, показываю-
|
|
|
Рис. 5.23 Ячеистая структура Al после обжатия на 10% |
|
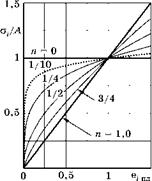
Рис. 5.24 Вид кривых нагружения материала при разных значениях показателя упрочнения n |
|
б а„ . кГ/мм 40 " |
|
о, 1 G-I |
4 |
|||||||
|
ч |
= |
-АІ |
пл) |
|||||
|
Е = 2,1-Ю А = 100 п = 0,2 |
- |
|||||||
|
1 1 |
||||||||
|
- Е-г,, |
|
30 20 10 |
|
0 0,2 0,4 0,6 0,8 1,0 |
|
е,-, % |
|
Рис. 5.25 Схемы распространения полос сдвига (а) и начального участка кривой нагружения (б) |
щих при испытаниях прочность, близкую к теоретической прочности. Деформация сосредоточена в темных участках, где плотность дислокаций столь велика и они так перепутаны, что произвести какой-либо анализ сопротивления их движению невозможно. Поэтому мы в своих работах для описания наклепа пользовались формулой (5.40), но параметры кривой упрочнения А и n определяли экспериментально:
^ - a • еПпл, (5.40)
где е;, пл — интенсивность пластической деформации.
Кривые нагружения, вычисленные по формуле (5.40) при разных показателях упрочнения n, построены на рис. 5.24.
Видно, что при n = 0 формула (5.40) описывает идеальный жестко-пластический материал с пределом текучести стт = А. Случай n = 1,0 соответствует материалу с линейным упрочнением — такие материалы мне не встречались. Для конструкционных сталей показатель упрочнения обычно находится в пределах 0,1 < n < 0,25. Чем прочнее сталь, тем меньше у нее n.
Но формула (5.40) не дает ни предела текучести, ни площадки текучести, ни предела прочности.
Резкий предел текучести обычно наблюдается у предварительно состаренных конструкционных сталей. Начальный участок диаграммы нагружения гладкого образца из такой стали показан на рис. 5.25б.
По оси абсцисс на этом графике отложена полная деформация, равная сумме упругой деформации siy и пластической деформа-
ции ег, пл. Пунктирная наклонная кривая соответствует упругой деформации. По закону Гука: = E ■ г1у.
Когда нагрузка достигает верхнего предела текучести а?, происходит резкий срыв напряжений до уровня нижнего предела ан. При этом от одной из галтелей прорастает на все сечение образца первая (из показанных на рис. 5.25, а жирными линиями, наклоненными под углом 45° к оси образца) полоса сдвига. Интенсивность пластического сдвига в этой полосе скольжения определяется формулой (5.40):
|
1
|
(5.41)
где sL — деформация Людерса, названная так в честь первооткрывателя этих полос сдвига2.
Образование соседней полосы сдвига уже не требует повышенных напряжений и происходит при напряжениях, близких к нижнему пределу текучести. Поэтому когда полосы сдвига захватывают все большую длину рабочей части образца, напряжения практически постоянны и лишь немного колеблются около ан. Только после того, как полосы сдвига распространятся на всю длину образца и весь металл будет деформирован на sL, с дальнейшим увеличением деформации начинается рост нагрузки по формуле (5.40). При расшифровке экспериментальной диаграммы нагружения в этой части из полных деформаций нужно вычитать как упругую деформацию захватов испытательной машины, так и г1у, чтобы получить пластическую деформацию, входящую в формулу (5.41).
Если на поверхности образца имеется риска, или образец плохо центрован в разрывной машине, то верхний предел текучести либо резко снижается, либо вовсе незаметен. Зуб и площадка текучести исчезают после закалки или после предварительного наклепа материала. Сварщики обязательно должны учитывать это явление при моделировании термопластического цикла сварки на образцах. При растяжении гладкого образца стареющей стали невозможно получить равномерный наклеп, равный, например, el/2. В этом случае одна половина рабочей длины образца будет наклепана до sL, а другая останется неде- формированной.
2 В период «борьбы с космополитизмом» эти линии обязательно называли «линиями Чернова-Людерса»: предположительно русский инженер-металлург Чернов открыл их раньше. Но, как это часто бывает, русские открытия долгое время остаются миру не известными.