ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
МЕТОД РАСЧЕТА ТРЕБУЕМОЙ ПЛАСТИЧНОСТИ
Этот метод расчета разработан только для статически нагруженных конструкций с целью предотвращения их разрушения при низком уровне напряжений. Вводятся следующие определения:
1. Все поля напряжений а, существующие в конструкции, разделяют на две составляющие (рис. 7.5).
|
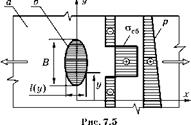
Схема разбивки конструкции на две зоны и поля напряжений на две составляющие |
р — номинальные напряжения, вычисляемые по правилам сопромата от полезной нагрузки. Эти напряжения определяются уравнениями равновесия внутренних и внешних усилий и не зависят от пластических деформаций металла в наиболее напряженных частях конструкции; асб — собственные напряжения, которые уравновешены в конструкции и которые перераспределяются (снимаются) при появлении пластических деформаций металла в наиболее напряженных частях конструкции. К собственным напряжениям можно отнести поля сварочных и реактивных напряжений, поля напряжений от местных изгибов, связанных со сварочными деформациями и смещениями кромок в стыковых швах, поля напряжений от конструктивной концентрации напряжений, если из них вычесть эпюру номинальных напряжений р, и т. п. По табл. 1.3 собственные напряжения определяют факторы: 1 — конструктивные концентраторы, 9 — термические напряжения, 11 — остаточные напряжения, которые фигурируют в 31% случаев разрушения сварных конструкций.
Таким образом, напряжения, действующие в любой части конструкции, являются суммой:
а = р + асб. (7.10)
2. Металл сварной конструкции также разделяется на:
основную часть конструкции, где напряжения а, в соответствии с нормами расчета на прочность, не достигают предела текучести, которая находится в упругом, обычно плоском, напряженном состоянии;
зону разрушения, в которой ожидается зарождение (инициация) разрушения, находящуюся в упругопластическом трехмер
ном напряженном состоянии. Хотя зона на рис. 7.10 показана в виде эллипса, она может быть любой формы. Ее ширину —размер, перпендикулярный направлению растяжения, — обозначим В, а длину — размер в направлении растяжения, переменный по ширине зоны B, являющийся некоторой функцией от координаты у, — обозначим через l. Будем считать, что эти размеры малы по сравнению с размерами конструкции.
Если основная часть конструкции состоит из ряда пересекающихся и последовательно соединенных друг с другом пластин, это не меняет логики дальнейших рассуждений.
Если в конструкции имеется целый ряд зон разрушения, то они могут анализироваться поочередно.
Напряженно-деформированное состояние сварной конструкции можно было бы теоретически рассчитать и без разделения ее на две части. Можно разбить ее на трехмерные упругопластические конечные элементы и на компьютере решать последовательно задачи о кинетике напряженно-деформированного состояния в процессе сборки, сварки, монтажа, действия полезной нагрузки и температурных воздействий. Но практически для достаточно крупной конструкции это невозможно. Слишком много придется ввести элементов и последовательных приближений при решении нелинейных упругопластических задач. Не хватит ни времени на подготовку исходных данных для такого решения, ни памяти, которой располагают компьютеры, ни времени на само решение.
Большая часть объема металла в любой сварной конструкции обычно находится в пределах упругости при одноосном или плоском напряженном состоянии. Практика показывает, что распределение напряжений и деформаций в этой части конструкции достаточно надежно может быть получено простыми методами расчета из теории сопротивления материалов. Для зон конструкции, где имеются конструктивные концентраторы напряжений, можно использовать плоские линейные решения метода конечных элементов, которые не требуют итераций и достаточно дешевы. Для приближенного расчета полей сварочных и реактивных напряжений можно использовать классическую одномерную теорию сварочных деформаций. Наконец, этими простыми методами расчета можно наметить границы зоны, где при нагружении конструкции возникают пластические деформации. Все перечисленные части конструкции, в которых пластических деформаций при приложении полезной нагрузкир не ожидается, отнесены к основной части конструкции.
Однако в некоторых небольших, по сравнению с основной частью конструкции, зонах возможны опасные дефекты. Чаще всего это непровары, технологические трещины или другие дефекты сварных соединений. Металл в этих зонах может быть доведен до пластического состояния еще до приложения напряжений p от полезной нагрузки за счет собственных напряжений. Вблизи корня этих дефектов действует трехосное напряженное состояние. Распределение напряжений может быть достаточно сильно искажено из-за формы сварных швов. Эти зоны отнесены к зонам разрушения. Для расчета их напряженного состояния потребуется решать трехмерные упругопластические задачи. Такие решения осуществимы только для сравнительно небольших размеров моделируемой части конструкции.
Однако если решение упругопластической задачи для зоны разрушения недоступно, или оно мало достоверно, то можно смоделировать эти зоны на сравнительно небольших образцах, разрушить эти образцы и получить представление о прочности и пластичности этих зон.
Дальше останется только объединить решение, полученное для основной части конструкции и сведения о прочности и пластично-
|
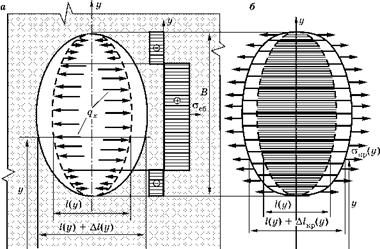
Рис. 7.6 Схема упругих перемещений Л1у границ между зонами при снятии собственных напряжений осб с зоны (а) и схема распределения прочности окр и пластической податливости Л1кр зоны разрушения (б) |
сти зоны разрушения, затем установить, наступит ли для зоны разрушения опасное состояние по напряжениям, действующим на ее упругопластической границе или по перемещениям этой границы. На рис. 7.6 слева показана часть основной упругой зоны конструкции, из которой «вырезана» зона разрушения.
Начальное положение отверстия, полученного от этой операции, показано прерывистой кривой линией. Рядом с контуром этого отверстия (контуром упругопластической границы), с размерами B и l(y), показана эпюра собственных напряжений асб, действовавших в зоне разрушения. Чтобы в упругой задаче снять эти напряжения с контура упругопластической границы, нужно к этому контуру приложить распределенную нагрузку qx, равную снимаемым собственным напряжениям, но противоположную по знаку. Тогда на границе ссб + qx = 0.
|
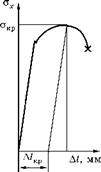
Рис. 7.7 Схема диаграммы нагружения образца из зоны разрушения |
Эта нагрузка показана на рисунке стрелками, приложенными к контуру. Там, где было растяжение, qx давит на контур, а где было сжатие — тянет контур внутрь отверстия от вырезанной зоны разрушения.
Под действием нагрузки контур будет получать перемещения. В результате начальный размер l(y) получит приращение Aly(y), и после снятия собственных напряжений станет равным l(y) + Aly(y), как показано на рисунке жирной сплошной линией.
Справа на рис. 7.6 показана вырезанная зона разрушения. Ее можно разрезать на полоски и каждую полоску испытать на растяжение. Схема диаграммы растяжения показана на рис. 7.7.
По оси абсцисс отложено удлинение образца в мм. По оси ординат — условные напряжения ax = Nx/A0; где Nx — нагрузка на образец в направлении оси х рис. 7.6; А0 — начальное поперечное сечение образца.
За критическое для зоны разрушения напряжение скр принято максимальное условное напряжение (предел прочности). Соответствующее этой точке кривой удлинение называется пластической податливостью зоны разрушения и обозначается А1кр.
Участок кривой нагружения с потерей устойчивости пластических деформаций отбрасывается в запас прочности и пластичности. Как следует из рисунка, аналогично отбрасываются упругие деформации образца и деформации, связанные с податливостью захватов машины.
Полученные при испытаниях образцов значения А1кр(у) и сткр(у) можно нанести на рисунок зоны разрушения в правой части рис. 7.6. Нанесенные на рисунке при координате у стрелки равны сткр(у), а длина зоны разрушения в этом месте — l(y) + А1кр(у).
|
(7.11) |
Сравнивая далее результаты, полученные для основной части конструкции, с результатами для зоны разрушения, можно записать два условия прочности, которые должны выполняться для каждой полоски зоны разрушения:
А1(у) < А1кр(у); р(у) < ^кр(у).
Второе неравенство справедливо, поскольку при выполнении первого все собственные напряжения будут сняты раньше, чем удлинение зоны разрушения достигнет опасной величины. Останутся только напряжения от полезной нагрузки, которые обычно линейно связаны с координатой у, как показано на рис. 7.5.
В этой формулировке есть одна неточность. Если для образцов из зоны разрушения нарезать очень узкие полоски, то в месте образования трещины исчезнут напряжения ау. При этом резко снизится жесткость напряженного состояния ^ металла в месте инициации разрушения и повысятся переходные температуры Тнп и ТМ. Пластическая податливость будет завышена.
Ширину образцов нужно выбирать такой, чтобы правильно моделировать на них жесткость напряженного состояния в опасных точках.
Такова точная постановка задачи. Но ее можно решить только в том случае, если задачу о деформациях основной части конструкции (левая часть рис. 7.6) решать методом конечных элементов.