ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ

КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ

3.1. ВЫЧИСЛЕНИЕ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ У ДЕФЕКТОВ ПО НЕЙБЕРУ

3.1.1.

КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ И ТИПЫ ЗАДАЧ

Согласно табл. 1.3 с концентрацией напряжений связано 7 фак­торов (с 1 по 7) и 38% всех аварий.

Метод решения задач о концентрации напряжений, разрабо­танный Г. Нейбером, сводится к следующему. Было доказано, что уравнения, приведенные выше в разделе 2, выполняются для пло­ской задачи, если напряжения вычисляются по формулам:

d2F

Ox =

dy2 = д2 F

°У = дх2 * (3.1)

_ = д2 F

Oxy дх ■ду,

где F — функция напряжений.

Доказано, что функция напряжений в плоской задаче может быть выражена через две гармонические функции Ф0 и Ф1 уравне­нием

F = Ф0 + х Ф1.

Гармоническими называются такие функции, которые удов­летворяют дифференциальному уравнению АФ = 0, где гармони­ческий оператор А имеет вид

A.JL+Л.

дх2 ду2

Так как интеграл от напряжений по координате дает вектор соответствующего усилия, функцию напряжений нужно подобрать так, чтобы на свободных от сил границах были бы справедливы граничные условия:

dF _ 0 и dF _ 0

эх - 0 и эу _ °. (3.2)

В случае одноосного растяжения напряжениями р вдоль оси х из (3.1) имеем

~ _^2F_„ -52F_0; т д2f _0

°х ду2 Р; °у дх2 ху дх • ду

Этим уравнениям удовлетворяет функция напряжений вида:

F = 2• у2; Фс -2.(у2 - х2); Фі = 2.х. (3.3)

Контур концентратора можно описать уравнением вида: ус = Дхс). Для того чтобы решить задачу о распределении напряжений в рас­тянутой пластине с концентратором, нужно к функции напряже­ний (3.3) добавить такую затухающую гармоническую функцию F*, которая позволила бы на контуре концентратора удовлетворить граничным условиям (3.2) при х = хс и у = ус:

d( F + F*) = с и d(F + F *) = dx dy '

Естественно, что функцию F* найти значительно проще, если граница совпадает с направлением координаты, например ус = const или хс = const. Чтобы получить это преимущество, Г. Нейбер реша­ет задачи в криволинейных координатах (и = и(х, у) и v = v(x, у)), у которых функции от декартовых координат х, у выбраны так, чтобы контур концентратора совпадал с уравнением либо и = ис = = const, либо с уравнением v = v0 = const.

Кроме того, желательно, чтобы система криволинейных коор­динат была бы ортогональна. Чтобы кривые и(х, у) = const; и кри­вые v(x, у) = const везде пересекались бы под прямым углом. То­гда дифференциальные уравнения теории упругости, полученные для декартовой системы координат, останутся справедливыми и для криволинейной системы координат.

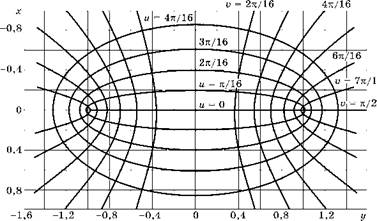
Например, на рис. 3.1 представлена система эллиптических координат (и, v), которые связаны с декартовыми координатами (х, у) формулами:

х = sh^) • cos(v); у = ch^) • sin(v), (3.4)

—g 2

р—и 2"

Из рисунка видно, что контур внутреннего эллиптического от­верстия в этих координатах задается выражением и = ис; а контур внешней гиперболической выточки задается уравнением v = v0.

ри і e

Л(и) = -------------- косинус гиперболический и.

Уравнения эллипсов и гипербол рис. 3.1 в декартовых коорди­натах легко получить, если из формул (3.4) исключить и или V.

Чтобы исключить координату V, возведем обе части уравнений (3.4) в квадрат и решим их относительно тригонометрических функций:

Далее, зная, что sin2(v) + cos2(v) = 1 и суммируя правые части уравнений, получим уравнения для эллипсов при и = const.

Аналогично, если решить уравнения (3.4) относительно гипер­болических функций, то, зная, что ch2(u) - sh2(u) = 1, можно по­лучить уравнения для гипербол при v = const:

х“

= 1;

sh2(u) ch2(u)

У2 х2

- = 1.

sin2(v) cos2(v)

Рис. 3.1 построен на MathCad по формулам (3.5).

Эллиптические координаты рис. 3.1, как и декартовы коорди­наты х, у, ортогональны. Линии u = const и v = const везде пересе­каются под прямым углом. Поэтому, чтобы перейти от (ах, ау, тху) к (au, av, xuv), по формулам (2.12) нужно определить направляю­щие косинусы.

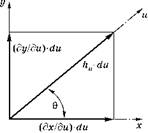
Из рис. 3.1 видно, что масштаб пря­моугольников du ■ dv увеличивается при удалении от начала координат. Поэтому при определении косинуса угла 0 между координатами и и х нужно ввести коэффи­циент искажения hu (масштабный множи­тель для координаты и). Связь прираще­ния du координаты и c приращениями dx и dy декартовых координат показана на рис. 3.2.

Для совмещения этих приращений в декартовых координатах приращение ко­ординаты du нужно умножить на масштабный множитель hu, на­зываемый коэффициентом искажений по координате и.

Из рис. 3.2 видно, что:

cos(0)-ти±; sin(0)-%h. ■

Возведя эти равенства в квадрат и суммируя, можно вычис­лить hu. Проделав эти же операции для координаты v, можно по­лучить аналогичную формулу для коэффициента искажения hv по координате v. В результате имеем:

Из последних формул видно, что для эллиптических коорди­нат коэффициенты искажения равны друг другу:

h2 = h2 = h2 = sh2 (и) + cos2 (v).

Криволинейные координаты, у которых коэффициенты иска­жения равны друг другу (hu = hv), называются изометрическими.

Для нахождения полей напряжений у выступов и мелких внеш­них выточек Нейбер использовал вторую систему криволинейных координат:

11-

x = и-

y = V (1 -

Для области ( и2 < 1, V < 1) эти координаты графически пред­ставлены на рис. 3.3.

Видно, что кривая v =1 соответствует очень пологому выступу, похожему на валик качественно выполненного сварного стыкового шва. Кривая v = 0,2 соответствует сварному валику с наплывами. При дальнейшем уменьшении v наплывы увеличиваются.

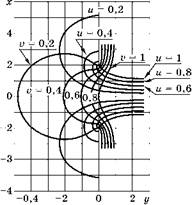
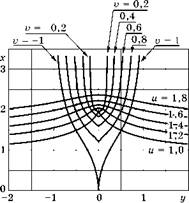
В области (и > 1) кривые и = const могут описывать мелкие по­верхностные выточки различной остроты (рис. 3.4). Материал тела с концентратором находится выше линии его границы и = const.

В случае и = 1 получается выточка с нулевым радиусом закруг­ления в корне. При дальнейшем увеличении и острота выточки быстро уменьшается.

Система криволинейных координат (3.9) тоже ортогональна. Подстановка (3.9) в (3.7) показывает, что эти координаты изомет­рические, и коэффициент искажений для них составит:

h2 = h2 = h2 = 1

(u2 + v2 )2

Если известна функция напряжений F, то напряжения в кри­волинейных координатах можно вычислять по формулам: