ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ЭФФЕКТИВНЫЙ КОЭФФИЦИЕНТ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ
Эффективным коэффициентом концентрации напряжений р при расчетах на усталость называется отношение предела усталости гладкого образца (a-L) к пределу усталости образца с концентратором (ct-l, K) при знакопеременном симметричном цикле (г = -1):
r ст-1
Р=^1К' (6Л78)
Причем в сварных конструкциях принято определять CT-L не для полированного образца, как это делают в машиностроении, а для пластины с прокатными поверхностями и кромками, обработанными путем строжки или фрезеровки.
Эксперименты показывают, что эффективный коэффициент концентрации р равен теоретическому коэффициенту концентрации kT, который вычислен для однородного упругого тела соответствующей формы методами, приведенными в разделе 3, только при достаточно больших радиусах кривизны концентратора р в месте зарождения трещины. Чем меньше р, тем меньше р по отношению к йТ.
При теоретическом вычислении эффективного коэффициента концентрации этот экспериментальный факт описывают с помощью теории макронапряжений.
Разрушение при многоцикловой усталости не может развиваться в математической точке, где вычисляются теоретические максимальные напряжения при решении задачи теории упругости. Для образования стабильных полос сдвига в наиболее слабом зерне металла (см. ранее) необходимо, чтобы средние по этому зерну напряжения удовлетворяли условию микротекучести. Таким образом, приложенные к металлу максимальные напряжения следует усреднять, по крайней мере, по сечению этого зерна. Но возможно, что напряжения в соседних зернах определяют условия микротекучести в наиболее слабом зерне. Тогда напряжения следует усреднять по большему количеству зерен.
Структурным элементом материала при расчетах на усталость называют такой минимальный объем металла, в котором еще может развиваться механизм разрушения, характерный для обычного образца из этого металла, подвергнутого испытаниям на усталость. Если форму структурного элемента описывать сферой, то размер структурного элемента определяется радиусом структурного элемента р*.
Макронапряжением S при усталости называется интенсивность напряжений стг, усредненная по объему структурного элемен-
та V* = (4/3) ■ л ■ (р*)3:
|
|
(6.179)
В плоской задаче структурный элемент можно представить цилиндром с радиусом р* единичной длины. Тогда V* = л ■ (р*)2.
По теории макронапряжений разрушение при симметричном цикле наступает тогда, когда выполняется условие
|
(6.180) |
S - ст-1, N,
где ст_!, N — предел усталости, найденный экспериментально при испытаниях обычных гладких образцов.
Но вычислять интеграл по формуле (6.179) даже в случае, когда имеется готовое решение задачи теории упругости для рассматриваемого концентратора, сложно. Попробуйте подставить в эту формулу какое-либо решение из раздела 3, и вы в этом убедитесь. Поэтому в литературе применяются различные способы упрощения данной задачи. Так, за макронапряжение S принимают напряжения в центре структурного элемента. Тогда S можно вычислить как напряжение в точке минимального сечения, находящейся на расстоянии р* от вершины концентратора. Очевидно, что этот способ справедлив только тогда, когда изменением градиента напряжений в пределах структурного элемента можно пренебречь. Наверное, это справедливо при р* ^ р.
Когда р* по порядку величины близок к р, более правильно находить макронапряжения, усредняя вычисленные при решении плоской упругой задачи напряжения в направлении развития ожидаемой трещины x на расстоянии 2р* от вершины концентратора:
|
|
Этот интеграл вычислять значительно проще, чем интеграл в формуле (6.179). В литературе можно найти и другие предложения по определению макронапряжений S.
В простейшем случае можно предположить, что при радиусе закругления надреза р ^ р* реальный радиус надреза перестает влиять на выносливость, а при р » р* эффективный коэффициент концентрации р совпадает с теоретическим коэффициентом концентрации йт для упругой задачи.
|
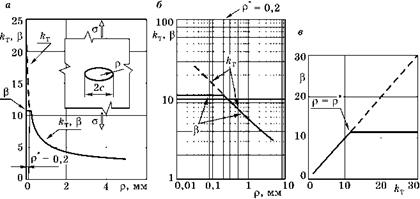
Рис. 6.86 Связь между эффективным р и теоретическим kT коэффициентами концентрации напряжений |
Радиус структурного элемента р* можно определить по результатам испытаний на усталость образцов с разными радиусами р, определяя экспериментальное значение р по формуле (6.178). Эффективный коэффициент концентрации при прочих равных условиях должен возрастать при уменьшении радиуса закругления р в вершине надреза. Но как только радиус р достигает предельного значения р*, р перестает увеличиваться. Это критическое значение радиуса р можно назвать «радиусом структурного элемента» и считать постоянной материала.
Поясним это на примере. Для эллиптического отверстия в широкой растянутой пластине (рис. 6.86а) теоретический коэффициент концентрации определяется формулой
|
(6.181) |
kT = 1 + 2 • с,
где 2с — размер отверстия в направлении, перпендикулярном нагрузке; р — радиус его кривизны в опасной точке.
На рис. 6.86а, б приведены кривые зависимости коэффициента kT от радиуса в вершине надреза р при глубине дефекта 2с = 10 мм. Для стали Ст3 можно считать, согласно Г. Нейберу, что радиус структурного элемента составляет около р* = 0,2 мм. Тогда при р > 0,2 мм и теоретический и эффективный коэффициент концентрации равны и вычисляются по формуле
kT = Р = 1 + 2 —.
Предельное значение эффективного коэффициента концентрации напряжений при р<р* = 0,2 мм составит
|
|
(6.182)
При дальнейшем уменьшении радиуса надреза эффективный коэффициент концентрации не зависит от остроты надреза.
На рис. 6.86в показана зависимость эффективного коэффициента концентрации от теоретического. Когда теоретический коэффициент концентрации достигает своего предельного для данного материала значения, эффективный коэффициент концентрации перестает возрастать.
Но это имеет место только при постоянном размере дефекта. Если в формуле (6.182) размер с увеличить до 10 мм, то:
|
|
Это явление нужно обязательно иметь в виду при оценке концентрации напряжений у сварных соединений. Часто для угловых швов в литературе приводятся значения р для предельной остроты надреза. В этом случае обязательно нужно уточнить, для какой стали в каком состоянии и для каких катетов шва и какой толщины листа эти коэффициенты экспериментально установлены. Если в конструкции катет шва в два раза больше, или предел текучести стали в два раза больше (это получено за счет измельчения зерна и соответствующего уменьшения р*), есть все основания считать, что значение р для этой конструкции будет больше указанного в литературе.
Вследствие приведенных выше соображений для расчета р по известному значению kT Г. Нейбер получил простую формулу
|
|
(6.183)
Р. Б. Хейвуд в монографии «Проектирование с учетом усталости» поместил многочисленные таблицы результатов экспериментального определения предела усталости многих сталей с преде-
лом прочности от 41 до 105 кг/мм2 разных авторов. Результаты
получены на полированных цилиндрических образцах разных диаметров с концентраторами в виде поперечных отверстий, галтелей и кольцевых надрезов различной глубины и остроты. Испытания проводились как на осевое растяжение-сжатие, так и на
изгиб. Предел усталости определялся на базе N = 107 циклов, в то время как для сварных конструкций базовое число циклов принимается равным 2106 циклов (см. формулу (6.156) и рис. 6.73). Таблицы этой книги являются прекрасным материалом для проверки работоспособности различных формул, предлагаемых в литературе для вычисления коэффициента р.
В результате обработки этих результатов Р. Б. Хейвуд, как и многие другие исследователи, пришел к выводу, что точность формулы (6.183) недостаточна, так как на накопление повреждений в структурном элементе влияет не только среднее напряжение, но и градиент напряжений. Приближенный учет влияния градиента напряжений привел Р. Б. Хейвуда к выражению
Р = k----------------------
|
|
|
1 + - |
|
Jlrp |
kr -1, 2, РІ (6.184)
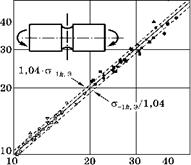
Рис. 6.87
Сопоставление расчета предела усталости по формуле (6.184) и результатов экспериментов при изгибе круглых образцов с кольцевым надрезом n — количество серий образцов.
|
®-lk, Э
|
Результаты выполненной мною проверки работоспособности этой формулы по упомянутым выше таблицам книги Хейвуда представлены на рис. 6.87.
По оси абсцисс на этом рисунке (в логарифмическом масштабе) отложены экспериментальные (ст_1, k, Э) значения предела усталости образцов с концентратором напряжений, взятые из таблиц книги Хейвуда. По оси ординат в таком же масштабе отложены результаты моего расчета (ст_1, k, Р) на MathCad по формуле (6.184). Каждая точка этой таблицы отражает результаты испытаний одной серии образцов с обработкой вида, показанного в табл. 6.8 и на рис. 6.72. Всего на рисунке 62 точки или 62 результата испытаний 62 серий образцов с базой 107 циклов. Трудно представить величину объема экспериментальной работы, послужившей основой для этого рисунка.
В таблице под этим рисунком помещены пояснения. В первой колонке показаны обозначения точек, различные для разных сталей. Исходные значения предела прочности аВ и предела усталости гладких образцов ст_1 в кг/мм2 взяты из таблиц книги Хейвуда и даны во второй и третьей колонках этой таблицы. В четвертой колонке таблицы показано отношение о_1/оВ = л, которое входило выше во многие расчетные формулы. Значения теоретического коэффициента концентрации напряжений kT для каждого образца при вычислениях взято из упомянутых таблиц книги Хейвуда.
Значения радиуса структурного элемента р* для каждой серии образцов я определял, варьируя р* и находя значение, при котором относительная среднеквадратичная погрешность
|
|
становится минимальной. В этой формуле n — количество серий образцов разной формы для каждой стали, приведено в таблице; ст_1, k, Э — результат эксперимента; ст_1, k, Р — результат расчета по формуле (6.184).
Полученные таким образом оптимальные значения радиуса структурного элемента р* (мм) и среднеквадратичной погрешности расчета для каждой стали 8 (%) показаны в пятой и шестой колонках таблицы рисунка. Наконец, в последней колонке этой таблицы по ссылкам книги Хейвуда приведены фамилии авторов, испытавших указанные серии образцов.
Точное совпадение расчетных и экспериментальных результатов соответствует на этом рисунке наклонной сплошной прямой
линии. Пунктирными линиями показана полоса среднеквадратичных отклонений, вычисленная для суммы квадратов погрешностей всех 65 точек рисунка. Эта погрешность оказалась равной 6,2%.
Из рисунка следует, что совпадение результатов расчета предела усталости образцов с концентратором напряжений по формуле (6.184) хорошо совпадает с результатами экспериментов.
Cреднеквадратичная погрешность для всех 62 точек графика составляет 8 = 3,94%. Это определяется тем, что из всех результатов, помещенных в книге Хейвуда, я взял только относящиеся к цилиндрическим образцам с кольцевым надрезом, для которых имеется многократно проверенное надежное решение упругой задачи Г. Нейбера. Учитывая, что точное соосное нагружение таких образцов при растяжении-сжатии трудно выполнимо, я использовал при построении этого рисунка только результаты испытаний на изгиб, где центровка усилия не нужна. Наверное, сказалось и то, что образцы полированы и изготовлены достаточно точно.
Рассматривая численные значения р*, помещенные в таблице под рисунком, видно, что они по порядку величины почти везде совпадают с характерными значениями величины зерна для этих статей. Исключение составляют только две стали с пределом прочности 101 и 105 кг/мм2, для которых р* s 0,2 мм. Но для этих сталей испытано только по три серии образцов. Возможно, что этот результат связан с увеличенным разбросом результатов эксперимента, либо здесь влияет размер аустенитного зерна. Поэтому разумно заключить, что радиус структурного элемента составляет 1-3 диаметра зерна.
|
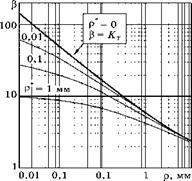
Рис. 6.88 Зависимость р от радиуса р при разных р*: |
Теперь рассмотрим, как уточнение, связанное с формулой
(6.184) , изменило классическую схему влияния остроты надреза на эффективный коэффициент концентрации (рис. 6.84).
Результаты вычислений по формуле (6.184) для эллиптического надреза глубиной с =5 мм при разных значениях радиуса структурного элемента р* приведены на рис. 6.88.
|
ц = 0,448; с = 5 мм. |
Из него видно, что резкого излома линий при р = р*, изображенного на рис. 6.86б, на самом деле нет. Кроме того, предельные
значения радиуса надреза (когда зависимость р от р становится горизонтальной) достигаются не при р = р*, а при р < р*/1000. Это видно по кривой на рис. 6.88, вычисленной для р* = 1 мм.
|
э |
0.48 |
• ■ |
▲ |
|||
|
□ |
X |
|||||
|
V |
||||||
|
40 60 80 100 ов Рис. 6.89 Зависимость отношения ^ = o_1/oB от предела прочности |
Но все описанные результаты расчета получены относительно предела усталости гладкого полированного образца. Поэтому они подходят только для деталей из однородного материала с достаточно гладкой (полированной) поверхностью.
Применительно к расчету сварных конструкций нужно заметить, что в таблице на рис. 6.87 коэффициенты ^ гораздо выше, чем в случае расчета сварных конструкций, когда за основу берется предел усталости образцов с прокатной поверхностью. Зависимость коэффициента ^ = a_1/aB, приведенного на рис. 6.87, от предела прочности стали построена на рис. 6.89 (обозначения точек те же).
Из рисунка видно, что среднее значение коэффициента ^ (сплошная горизонталь) равно 0,48. Хейвуд при приближенных расчетах считает для полированных образцов ^ =0,5. Это значительно большее значение, чем для гладких образцов с прокатной поверхностью, для которых приближенно принимают ^ = 0,3. Последнее значение на рис. 6.89 показано прерывистой горизонтальной линией.
Так как предел прочности практически не зависит от состояния поверхности (потеря устойчивости пластических деформаций к ней не имеет отношения), можно считать, что прокатная поверхность создает при испытаниях на усталость начальную эффективную концентрацию порядка р0 * 0,48/0,3 = 1,6. Таким образом, если появление ожидаемой трещины усталости в сварном соединении ожидается на гладкой оплавленной поверхности, а ст_1п, как всегда, определено на образцах с прокатной поверхностью, то при расчете эффективного коэффициента концентрации значение коэффициента р, вероятно, следует разделить на р0 = 1,6. Это связано с тем, что предел усталости пластины с прокатной поверхностью ст_1, п меньше предела усталости ст_1 образцов с полированной поверхностью: ст_1,п = ст_1/р0.
Но если об этой поправке автор норм не имеет представления, то он может пытаться учесть ее, задавая у дефекта не реальный
радиус р, а эффективный радиус peff. Оценим эту поправку к радиусу на примере эллиптического дефекта. Условие равенства прочностей выразится в виде: йс(р) = 1,6 ■ ka(peff) или:
|
|
Решая это уравнение относительно peff, получим Peff _ 1,62 ■ (t/р)
|
|
(6.185)
Из формулы (6.185) следует, что при остроте надреза t/p = 1, для компенсации концентрации от прокатной поверхности следует увеличить эффективный радиус в 5,2 раза по сравнению с реальным радиусом р. Если острота надреза будет t/p = 100, то эффективный радиус должен быть в 2,7 раза больше р. Возможно, что этим частично объясняются большие значения радиусов закругления, которые используют некоторые авторы при попытке вычислить эффективные коэффициенты концентрации для сварных соединений.
Конечно, приведенное здесь значение р0 только ориентировочное. Но при расчетах на усталость мест конструкции с концентратором обязательно следует учитывать различия в состоянии поверхности металла в вершине концентратора и состоянии поверхности гладких образцов, при испытаниях которых определялось значение а_1, использованное в расчетах.