ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ДВУСТОРОННЯЯ ГЛУБОКАЯ ГИПЕРБОЛИЧЕСКАЯ ВЫТОЧКА ПРИ ОДНООСНОМ РАСТЯЖЕНИИ
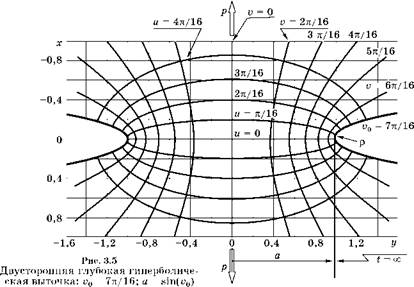
Схема двусторонней глубокой внешней выточки с координатой контура v0= 7я/16 показана на рис. 3.5. Предполагается, что при v < v0 материал распространяется до бесконечности. Поэтому глуби-
|
|
на выточки t с обеих сторон равна бесконечности (см. рис. 3.5). Вдали от выточки материал растянут усилием Px (широкие стрелки).
Если средние напряжения в минимальном сечении обозначить черезр, а толщину пластины— через d (рис. 3.5), то усилие Px вычисляется по формуле
Px =р • 2 • a • d. (3.12)
Распределение напряжений определяется по формулам
«и. A■ch(u)■ cos(v)■(2 + cos2(v0>-cos2(v)
h2 Ч h2
|
(3.13) |
«V - hA2■ ch(u)■ cos(v)■(cos2(v)-2cos2(V"));
V, - A. sh(u)■ sin(v) (cos2(v»)-cos2(v)
h2 h2
где постоянная интегрирования A из условия равновесия определяется как
. sin(v0)
A - p-v„ + sin(v„)-cosv,). <314)
Острота выточки (а/p) связана с ее гиперболической координатой поверхности выточки v, выражением
tg2(v0) = a (3.15)
следовательно, зная остроту, можно определить sin(v0) и cos(v0), входящие в формулы для напряжений:
|
sin(v,) = cos(v,) = |
a/p ; a/p + 1;
1 (3.16)
a/p + 1"
Наибольший интерес представляет распределение напряжений в минимальном сечении (х = 0; ^ и = 0), где в силу симметрии Tuv = xxy = 0; ось х совпадает с направлением и: аи = ах = ст1; ось у совпадает с направлением v: av = ау = а2.
Если толщина пластины d мала по сравнению с радиусом в вершине выточки p, то можно считать, что при растяжении возникает плоское напряженное состояние: стг = 0.
|
|
Однако при исследовании вопросов прочности чаще приходится иметь дело с плоским деформированным состоянием: єг = 0. Тогда из третьего уравнения закона Гука следует, что:
=v-(ъх +Оу). (3.17)
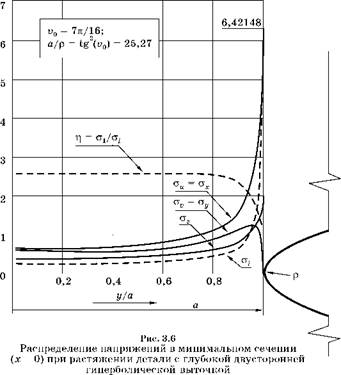
Распределение напряжений в минимальном сечении растянутой пластины с глубокими двусторонними гиперболическими выточками при плоской деформации, вычисленное на MathCad по формулам (3.13) при остроте выточки а/р =25,27, показано на рис. 3.6. Здесь же в масштабе изображен контур выточки такой остроты, с радиусом р и размером минимального сечения 2а. Сплошными линиями показаны эпюры трех главных нормальных напряжений.
Напряжения ох концентрируются у контура выточки. Так как мало нагруженные части пластины вдали от минимального сечения препятствуют сокращению размеров в поперечных направлениях, в минимальном сечении возникают растягивающие напряжения Оу и стг.
|
1 |
|
2 ф = (а/р)1/2 |
|
Рис. 3.7 Коэффициент концентрации напряжений для глубокой двусторонней гиперболической выточки при растяжении |
|
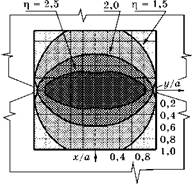
Рис. 3.8 Распределение жесткости напряженного состояния г| = о1/о; в области (-а < я < +а; - а < у < +а) при а/р = 25,27 |
Из рис. 3.6 видно, что коэффициент концентрации kax = amax/ p = 6,4. Для вычисления коэффициента концентрации у глубокой выточки Нейбер получил формулу
2-Ф-(Ф2 +1)
(3.18)
Ф + (ф2 +1) • arctg^)
где
Ф =
Зависимость коэффициента концентрации напряжений от параметра ф графически представлена на рис. 3.7. Результаты вычисления по формуле (3.18) показаны сплошной линией.
Видно, что при ф >3, эта кривая стремится к прямой:
, 50,93
k-= -44тф-
На свободной поверхности выточки (рис. 3.6) перпендикулярные этой поверхности напряжения ау обязательно равны нулю. Но при удалении от поверхности ау быстро нарастают, и на расстоянии 1,011 р от поверхности выточки эти напряжения достигают максимума (a„)max = 1,236 p. При дальнейшем приближении к центру детали они уменьшаются, приближаясь к напряжениям ах.
Напряжения аг при плоской деформации максимальны на поверхности выточки и при удалении от нее уменьшаются.
Пунктирными линиями на рис. 3.6 показаны распределения интенсивности напряжений а; и жесткости напряженного состояния ^ = ст1/стг. На поверхности выточки интенсивность напряжений а; всего на 15% меньше ст1. Но при углублении в материал интенсивность напряжений быстро уменьшается, так как уменьшаются разности между главными напряжениями. В результате жесткость напряженного состояния ^ = ст1/стг возрастает.
^ = ст1/стг — очень важная характеристика. Она показывает, во сколько раз упругие напряжения ст1 могут превосходить предел текучести при упругом нагружении материала. Так, из рис. 3.7 следует, что сталь с пределом текучести стт = 25 кг/мм2 в центральных частях детали с глубокими выточками остротой а/р = 25 перейдет в пластическое состояние только при ст1 = Л'стт = 2,56 • 25 = 64 кг/мм2.
На рис. 3.8 показано распределение жесткости напряженного состояния в окрестностях минимального сечения. Видно, что область материала с высокой (более 2) жесткостью ^ имеет форму ореха, занимающего почти все минимальное сечение детали с таким концентратором.