ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ДЕФЕКТЫ, РАСПРОСТРАНЕННЫЕ НЕ НА ВСЮ ТОЛЩИНУ
В сварных соединениях большинство дефектов (начальных трещинок, непроваров) не распространяются на всю толщину листа. Такие дефекты моделируются эллиптическими трещинами, плоскость которых перпендикулярна направлению внешней нагрузки.
|
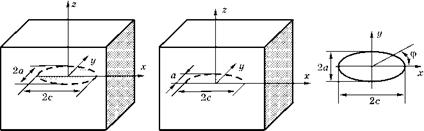
Рис. 3.38 Внутренняя эллиптическая и поверхностная полуэллиптическая трещины |
На рис. 3.38 показан весьма часто встречающийся в практике случай внутренней эллиптической трещины и поверхностной по - луэллиптической трещины.
В точке контура внутренней эллиптической трещины с углом ф (см. схему в правой части рис. 3.38) коэффициент интенсивности напряжений вычисляется по формуле
|
In - a |
|
(3.81) |
|
Ki =- |
|
Ф |
|
вт2(ф) + | —) - cos2^), |
|
2 |
где Ф — эллиптический интеграл, вычисляемый по формуле
ж/2
|
■Бт2(ф) -<іф = |
ф= IJ1 _
0
= _ [1 _ (а/с)2] 3 ■ [1 - (а/с)2]2
2(4 64
|
(3.82) |
С точностью до 1,5% можно считать, что Ф=1+^.{ а ).(1+1 а.
|
12 |
6 с
Наиболее опасная точка находится на малой полуоси эллипса (рис. 3.38), где ф = л/2:
|
К |
|
(3.83) |
|
I, max |
|
p-у я-а ф ■ |
Из формулы (3.81) видно, что минимальное значение К1 получается при ф = 0 на большей полуоси эллипса:
|
Ki |
ф V с ■
Здесь коэффициент интенсивности напряжений в (а/с)1/2 раз меньше, чем на малой полуоси. Вследствие этого вытянутая
усталостная трещина обычно растет в таких направлениях, чтобы ее контур приближался к дуге круга.
Если расчетный размер полуэллиптической или эллиптической трещины l = а, то из приведенных формул следует, что для внутренней эллиптической трещины коэффициент K-тарировки составляет:
Y = —
5 Ф’ (3.84)
а для поверхностной полуэллиптической трещины влияние свободной поверхности учитывают, как и для сквозной трещины, умножением коэффициента интенсивности напряжений на 1,12:
Ye - Y2 • Y5 = іф2. (3.85)
Кроме того, если необходимо, учитывают поправку на радиус пластической зоны по Ирвину.