ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
БЕСКОНЕЧНОЕ УПРУГОЕ ТЕЛО С ВНУТРЕННЕЙ СФЕРИЧЕСКОЙ ПОЛОСТЬЮ
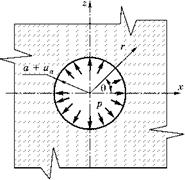
Сформулируем задачу: бесконечное тело с внутренней сферической полостью радиусом а нагружено внутренним давлением р, которое создает перемещение поверхности полости ur = ua (см. рис. 5.18).
Запишем граничные условия:
1. Вдали от полости внутреннее давление не должно вызывать перемещений материала. При r = да имеем:
|
|
А1 = 0.
2. На поверхности сферы заданы перемещения ur = ua. При r = a имеем:
|
А, |
|
|
|
и = ua л — |
|
аг = |
|
Рис. 5.18 Схема сферической полости радиусом а и внутренним давлением p |
|
- = Ua |
|
2 |
|
a |
|
А, = Ua ■ a2. Подставляя эти значения постоянных в (5.22) и (5.24), получим: |
|
2 |
|
-2 • (1 - 2 у) (1 - у-2 у2) (1 - 2 у) |
|
ua • a |
|
E |
|
ua • a |
|
• E • |
|
(1 - у-2 •у2) |
|
(5.26) |
|
Давление внутри сферы: p = _CTr,(r=a) : |
|
2 • (1 2 • v) e Ua |
|
(5.27) |
|
(1 - v-2 v2) |
|
Если давление известно, то |
|
'"x'a a |
|
(5.28) |
p (1 - v-2 v2) E'
2 • (1 - 2 •v)
Подставив это выражение в формулы (5.26), получим простые выражения для вычисления напряжений у сферической полости, нагруженной внутренним давлением:
|
(5.29) |
|
Стг =- |
=- p-i-a
Аналогично можно рассчитать и распределение напряжений в стенке толстостенного сферического сосуда. Для этого нужно будет просто вычислить новые значения постоянных А1 и А2 так, чтобы удовлетворить граничным условиям на внутренней и наружной поверхностях этого сосуда.