ОСНОВЫ ПРОЕКТИРОВАНИЯ. ХИМИЧЕСКИХ ПРОИЗВОДСТВ. И ОБОРУДОВАНИЯ

Термодинамический анализ процессов

Термодинамический анализ позволяет оценить:

• энергетическую возможность и направление протекания реакций;

• сопровождающие реакции тепловые изменения, позволяющие рассчитывать тепловые балансы процессов;

• предпочтительность реакций и устойчивость образующихся соединений;

• пути подавления нежелательных реакций и устранения по­бочных продуктов;

• выбор оптимального режима протекания реакций (темпера­туры, давления и концентрации реагирующих веществ).

7.2.1. Равновесие химической реакции

Константа равновесия, как постоянная величина, определяется че­рез равновесные активности компонентов реакции:

Ж=№*Л (7.1)

где Ка - константа равновесия, выраженная через равновесные активно­сти; а* - равновесная активность і-го компонента реакции; v, - стехио­метрический коэффициент /-го компонента с соответствующим знаком (минус - для реагентов, плюс - для продуктов реакции).

Большинство химических процессов протекает при практически постоянном давлении. В этом случае равновесие можно характеризовать энергией Гиббса (изобарно-изотермическим потенциалом). Изменение энергии Гиббса в процессе химической реакции описывается соотноше­нием:

AG = - RTIпШ-W + /Г/'In ГК'- (7.2)

Если исходные реагенты находятся в стандартном состоянии, т. е. Qi= 1, то второе слагаемое в уравнении (7.2) равно нулю и получается известная изотерма Вант-Гоффа:

AG° =-RTnKa, (7.3)

где AG0 - стандартное изменение энергии Гиббса.

Величину ДС/° можно определить по стандартным изменениям эн­тальпии и энтропии

AG0 =АН° - Ш°. (7.4)

Уравнения (7.3) и (7.4) являются основой для расчета равновесий. Следует указать, что при равновесии равно нулю AG, но не AG0, поэтому знак AG определяет направление реакции. При AG < 0 реакция идет в прямом направлении, а при AG > 0 - в обратном. При AG = 0 сис­тема находится в равновесии.

Стандартным состоянием для газов и паров принято считать иде­альное газовое состояние при давлении 101,325 Па» 0,1 МПа (1 ата) и при температуре 298,15 К (25 °С). Именно при этих параметрах приве­дены в термодинамических таблицах значения Д, ДЯ^, AS^.

Для химической реакции изменение энергии Гиббса, энтальпии и абсолютной энтропии можно вычислить как их сумму для продуктов ре­акции и реагентов с учетом знака стехиометрических коэффициентов:

Д^298 = Z v/AG/,298> Л^298 = Z ^уДЯуд98^ ^298 = ^Уі^іЛ98 • Обычно активность идеального газа равна отношению его парци­альных давлений в данном и стандартном состоянии:

В физической системе единиц pf =1 атм, поэтому безразмерная активность численно равна его парциальному давлению. При переходе к системе СИ это соответствие нарушается, вследствие чего

^(мпа)=^ки„)-0.101325^'

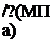■•^^ + EVi-ln(0,101325) = _^L-2,28942E

RT RT

Приближенный метод оценки константы равновесия для идеально­го газа дает соотношения

AG029s = AH°29s-TAS°29s; In

Ошибка в определении Кр в этом случае достигает 20 %, и тем вы­ше, чем выше температура процесса. Термодинамические функции за­
висят от температуры, что должно учитываться при точном расчете кон­станты равновесия для идеального газа.

Функциональная зависимость константы равновесия от температу­ры при постоянном давлении определяется уравнением изобары Вант - Гоффа

где А//1 - изменение энтальпии процесса в стандартном состоянии.

Если А/7° не зависит от температуры, что справедливо в узком ин­тервале температур, то уравнение (7.6) можно проинтегрировать. Интег­рируя его в пределах от Т до 72, получим

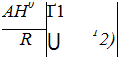
кр(т2)

КМ)

Отсюда видно, что если Т < Т2, то при эндотермической реакции Л К(Т2)

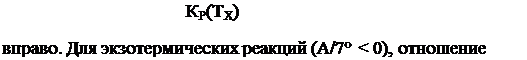(ATT > 0) отношение —----- больше единицы и равновесие сдвигается

КР(Т2)

КЛТХ) меньше единицы и равновесие сдвинуто влево.

Используя уравнение (7.7) для узкого интервала температур, мож­но найти значение константы равновесия для температуры Т2, если из­вестно аналогичное значение для температуры Т.

Более точное определение константы равновесия с учетом ее тем­пературной зависимости заключается в следующем. Для энергии Гиббса зависимость от температуры имеет вид:

Стандартное изменение энтальпии также зависит от температуры в соответствии с законом Кирхгофа:

d(AH°)

dT

где АСР - разность изобарных теплоемкостей продуктов реакции и реа­гентов, определяемых уравнением при учете стехиометрии

А Ср=^Срі.

Тогда стандартные значения энтальпии и энтропии примут вид:

т т АС

ДЯ» = ДЯ2% + J £CpdT; AS? = AS2% + J —£

298 298 L

При этом точное уравнение для энергии Гиббса будет

ДС/у1 = АН^ - TASy ;

Приближенным решением этого уравнения является решение, предложенное Темкиным и Шварцманом [68]. Метод основан на приме­нении регрессионного уравнения зависимости теплоемкости от темпера­туры вида:

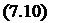С =а + ЬТ + сТ2

і у Z

где а, Ь, с и с_2 - постоянные для данного вещества.

Тогда, после использования последних, получается:

AGj = ДЯ298 - У'ДД298 - Т(АаМ0 + ДШ, + АсМ2 + Ас_2М_2)

где Mo, Mi, М2 и М_2 - интегралы, выраженные в виде

т dT т т dT т

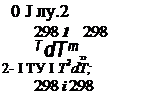j^jdT - Mj = j I TdT

298 I 298

_ dT T. dT

^-2 I r2 J r2

298 У 298 1

Формулы расчета этих интегралов для базисной температуры

Т0 = 298,15 К имеют вид:

Т Т (Т — Т Л2

М0 =1п---- ь —-1; ML = 0,0005--------

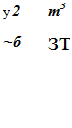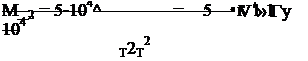Tq Т Т

Значения этих интегралов табулированы (см. например [68, 71]) в пределах от 300 до 3000 К через 100 К и могут использоваться при ин­терполяции.

Тогда уточненный расчет константы равновесия можно произвести по формуле

При повышенном давлении или при состоянии системы, близком к насыщенному пару, газы не могут считаться идеальными. В этом случае используют выражения констант равновесия и изотермы Вант-Гоффа через активности компонентов. Для этого вводится понятие летучести или фугитивиости/ удовлетворяющей условию

dG = - RTd( In/).

При этом стандартная летучесть/0 равна летучести газа в идеальном со­стоянии при давлении 101,325 кПа.

Активность - это отношение фугитивиости газа в данном и в иде­альном состоянии:

ft

fl

Коэффициентом активности газа называют отношение его фуги- тивности к парциальному давлению:

При давлении 1 атм реальный газ можно считать идеальным, по­этому /° = 1 атм. Тогда

Изотерму Вант-Гоффа для реальных газов можно привести к сле­дующему виду (Кр выражена в атм.):

AGj = - RTnKa = - RTnUa-v' = - Я7’1п(п рГ ' П У Г ) = - RTn(Kp • Ку).

Коэффициент активности определяется различными методами, ко­торые описаны в литературе по физической химии [68] или по расчету физико-химических свойств газов [20, 28, 29].

Коэффициент активности для реального газа можно найти по принципу соответствующих состояний. Согласно этому принципу зна­чения коэффициента активности для любых реальных газов являются одинаковыми, если они находятся при одинаковых приведенных темпе­ратуре и давлении (см. рис. 7.1). При этом

Т Р

Т =----------- 71 =----------------------- ,

Т V

*кр /кр

где т и п - приведенные температура и давление;

Тир - действующие температура и давление;

УКр и /Лер - критические температура и давление.

Данные по коэффициенту активности табулированы и имеются в литературе (см., например, [18]). Значения критических температур и давлений можно найти в литературе в специальных таблицах или рас­считать. Их расчет описан в [20, 28].

Изменение стандартной энергии Гиббса для жидкофазной реакции будет равно:

дс"=дог° + га-1п(пй")>

где Pi - парциальное давление пара і-го компонента над жидкостью.

Соотношение между константами равновесия в жидкой и газовой фазе составляет:

к„ = кр[пргУ,

где К„ - константа равновесия, выраженная через молярные доли ком­понентов, при этом Кп = ППГ (пі ~ молярная доля компонента).

Рассмотренный метод не пригоден для растворов сильно откло­няющихся от законов Генри и Рауля. К таким растворам относится большинство систем, представляющих практический интерес. В этом случае необходимо использовать константу равновесия, выраженную через коэффициенты активности [28].