ОБОРУДОВАНИЕ ЦЕЛЛЮЛОЗНО-БУМАЖНОГО ПРОИЗВОДСТВА

ПРОГИБ ВАЛОВ БУМАГО — — И КАРТОНОДЕЛАТЕЛЬНЫХ МАШИН

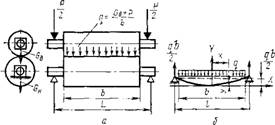
В процессе обработки движущегося полотна давлением в прессах и каландрах бумаго - и картоноделательных машин, а также в суперкаландрах нижние валы нагружены весом вы­шележащих валов и усилием дополнительного прижима. Про­гиб нижних валов, закрепленных в самоустанавливающихся под­шипниках, может в этом случае рассматриваться, как прогиб балки, закрепленной на двух шарнирных опорах (рис. 2.7).

При определении уравнения изогнутой оси вала влиянием объемных деформаций на характер и абсолютное значение про-

Гиба можно пренебречь (21]. Тогда прогиб вала у в любом се­чении равен ' '

У = Ум+У<з> (2.1)

Где ум — прогиб от действия изгибающего момента, мм; г/<г — прогиб от действия перерезывающих сил, мм.

Уравнение изогнутой оси вала и максимальный прогиб г/шах определяется на основании решения дифференциальных урав­нений изогнутой оси соответственно от действия изгибающего момента и перерезывающих сил:

= (2.3)

Где Е — продольный модуль упругости материала вала, Па; /ж — момент инерции рассматриваемого сечения вала, м4; Мх—■ изгибающий момент в рассматриваемом сечении, Н-м; G — мо­дуль упругости при сдвиге, Па; F — площадь поперечного сече­ния, м2; Qx — перерезывающая сила в рассматриваемом сече­нии, Н; | — коэффициент, зависящий от формы сечения вала (для круглого сечения £ = 1%).

Решение уравнений 2.2 и 2.3 имеет вид

(2.4)

Г/п = — <7 — , (2.5)

2 GF

Где q — интенсивность равномерно распределенной нагрузки, Н/м; b — длина рабочей части вала, м; I — расстояние между опорами вала, м.

Подставив зависимости (2.4) и (2.5) в равенство (2.1), по­лучим уравнение изогнутой оси вала с учетом действия изги­бающего момента и перерезывающих сил:

—— (Ш—362—2х2) + 48 EIX 2GF

Максимальный прогиб утах при х=6/2 для вала сплошного сечения равен

Второе слагаемое уравнений (2.6) и (2.7), равное прогибу вала от действия перерезывающих сил fn, может быть с достаточной для практики точностью определено из выражений /Wfc — b2//?2 для цельных валов и! м11я~Ъ21 (D2—dz) для пустотелых валов, где fM — максимальный прогиб вала от действия изгибающего момента.

Как следует из представленных зависимостей, влияние пере­резывающих сил на прогиб валов с малой длиной бочки более существенно, чем для валов большой длины.

Практически для бумагоделательных машин обрезной шири­ной более 2,5 м при определении закономерности прогиба двух- опорных валов влиянием перерезывающих сил можно прене­бречь (для валов с промежуточными опорами рубашки пере­резывающие силы следует учитывать [21]). Тогда для опреде­ления относительных значений прогибов (табл. 2.7) можно воспользоваться уравнением (2.4). Перейдя к безразмерной координате по формуле z = x/b и приняв t/b — a, имеем

У^-ЩГР^-ІЯ-*], (2.8)

В относительном виде

У* =-£-= —^ [г2 (За—1,5)—г4]. (2.9)

У max 12а —7

Приведенное уравнение удобно для определения численных значений ординат прогиба валов, нагруженных равномерно рас­пределенной нагрузкой.