разное

Процессы, протекающие в пеностекле в интервале температур отжига *

Расчет скорости охлаждения изделий из массивного стекла [297, 298] и пеностекла [14] рекомендуется проводить по фор­муле, разработанной и экспериментально проверенной А. Н. Даувальтером [84]:

3Rk (1 — (і) __ зЯд(І-р) (514)

A Ecyd? aEd2

Здесь v — скорость охлаждения, °С/ч; R — максимально допустимые напряжения на поверхности изделия, кгс/см2; % — коэффициент теплопроводности, ккал/(м-ч-"С)\ с — удельная теплоемкость, ккал!(кг-°С)-, а — коэффициент термического расширения, °С-1; у— плотность, кг/лг3; Е — модуль упруго­сти, кгс/см2-, р, — коэффициент Пуассона; d — полутолщина из­делий при двустороннем охлаждении, м\ a^Xjcy— коэффици­ент температуропроводности, м2/ч.

Приведенная формула учитывает лишь напряжения, возни­кающие при безопасном охлаждении изделия, но не учитыва­ет тех, которые остались в нем к моменту начала охлаждения. Разброс в значениях скоростей охлаждения пеностекла при от­жиге, рекомендуемых на основании расчетов или эксперимен­тальных данных (табл. 22), объясняется большой сложностью процесса и отсутствием экспериментальных данных о свой­ствах пеностекла в интервале температур отжига, необходи­мых для выполнения соответствующих расчетов.

Исследование теплофизических свойств. Из пеностекла, по­лученного на основе стекла 6Н, готовились образцы цилиндри­ческой формы радиусом 2,5 см и длиной 30 см. Скорость нагре­ва образцов составляла 3 °С/мин. Средние величины получен­ных значений коэффициента температуропроводности приведены в табл. 23. Данные при 0 °С получены путем экстра-

Исследование выполнено с участием кандидата технических наук В. И.

Пилецкого.

Полиции результатов эксперимента в области более высоких значений температуры. Величина теплопроводности пеностекла в исследуемом интервале температуры (20—500 °С).была рас­считана на основании зависимости а = К/су [203]. Значения удельной теплоемкости стекла при различной температуре при­няты из работ [94, 297]. Влияние удельной массы газа в пено­стекле при расчете не учитывалось.

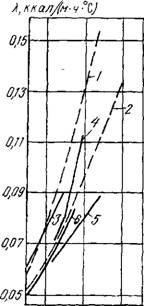
Результаты определений теплопроводности, выполненные различными авторами (рис. 5.16) [1, 94, 301, 302], и произве­денные нами расчеты показывают, что теплопроводность пено­стекла, как и других материалов с аморфной твердой фазой, подчиняется общей закономерности ее роста с повышением температуры. Приведенные в литературе данные только по объемной массе пеностекла не позволяют сопоставлять резуль­таты зависимости K=f(t), так как даже при одинаковой объемной массе на теплопроводность материала существенное влияние оказывают размер и форма пор, а также степень их

Связанности между собой [303]. Если, согласно работам А. Ф. Чудновского [302], Л. Л. Васильева и Ю. Е. Фраймана [305], в дисперсных материалах (размер тор 2—3 мкм) при небольших градиентах температуры эффектами конвективного переноса тепла и лучистой теплопроводности можно прене­бречь, то полученные нами данные подтверждают выполнен­ные И. С. Камерером [306] расчеты, а также данные, приво­димые Ф. Шиллом [1], о значитель­ном росте эффективной теплопро­водности газовой 'фазы при увеличе­нии диаметра пор в материале за счет опережающего увеличения лу­чистой теплопроводности.

Так как качественное пеностекло характеризуется большим количест­вом закрытых пор, давление газовой фазы в которых меняется при изме­нении температуры, то это также мо­жет влиять на характер изменения его теплопроводности. Данное пред­положение согласуется с результата­ми работы [307] о зависимости теп-

Рис. 5.16. Зависимость коэффициента тепло­проводности пеностекла от температуры по данным: 1, 2 — расчета; 3 — JI. М. Бутта и Э. 3. Житомирской [75]; 4 — 1. Хаазе [300]; 5 — В. Шулле [301]; 6 — фирмы Корнинг [2] ЮО 300 500 t^Z

Лопроводности некоторых теплоизоляционных материалов от давления и состава атмосферы.

Дилатометрические свойства пеностекла. Результаты иссле­дования (табл. 24) показывают, что коэффициент термическо­го расширения пеностекла соответствует коэффициенту тер­мического расширения исходного стекла, определенного по стандартной методике [304].

Полученное нами значение коэффициента термического расширения пеностекла 2Н близко к результатам исследований И. И. Китайгородского и Т. JI. Ширкевич [308], которые на аналогичном пеностекле получили значение а = 93-10~7 на образцах 10X10X50 мм. Значения температуры начала де­формации (7"н. д) и трансформации (Tg) при испытании образ­цов пеностекла имеют несколько больший разброс, чем у ис­ходных стекол, и не всегда отчетливо выражены при графиче­
ском изображении результатов эксперимента. Это можно объяснить влиянием структуры пеностекла на его деформатив - ную способность в области температур трансформации. Влия­ние толщины образца на его деформацию в области темпе­ратуры размягчения стекла ранее изучалось А. П. Заком [309], который установил, что уменьшение диаметра образца (стекловолокна) резко снижает температуру, соответствующую одинаковой деформации более массивного образца. Этим мож-

Но также объяснить снижение Ти. д пеностекла по сравнению с исходным стеклом (табл. 24).

Результаты исследования линейного расширения пеностек­ла указывают на близость термических свойств стекла и пено­стекла, что не соответствует выводам И. И. Китайгородского с соавторами [310] о большом разбросе в значениях коэффици­ента термического расширения пеностекла без какой-либо за­кономерности и совпадает с выводами Т. J1. Ширкевич [267] о соответствии термических свойств исходного стекла и пено­стекла.

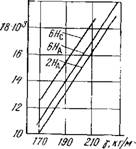
Зависимость механической прочности пеностекла от темпе­ратуры. При определении термомеханических характеристик образцы пеностекла, предназначенные для испытаний на сжа­тие, помещались в трубчатую печь, обеспечивающую изотер - мию образца и передачу на него усилий сжатия. Испытуемые образцы (7X7X7 еж) нагревались со скоростью 3 °С/мин и последующей выдержкой при температуре опыта в течение 20 мин. Для учета влияния объемной массы образцов на проч­ность пеностекла полученные результаты выражались в едини­цах эффективной (приведенной) прочности (Япр), равной от­ношению прочности к объемной массе. Они показаны на рис. 5.17 в виде зависимости Rnp=f(t).

При испытании образцов пеностекла на изгиб рабочий ор­ган машины МИИ-100 находился в печи с регулируемой тем­пературой. После установки образцов размером 4X4X16 см
печь разогревалась со скоростью 3° С/мин до температуры опыта, которая поддерживалась на достигнутом уровне в те­чение 20 мин.

Полученные данные (рис. 5.17) позволяют сделать вывод о том, что прочность пеностекла с повышением температуры плавно уменьшается, не обнаруживая резких изменений в ис­следованном интервале температуры. Некоторое ускорение снижения прочности у пеностекла 2Н при температуре 500 °С

Связано, по-видимому, с прибли­жением к области трансформации стекла.

Влияние температуры на проч­ность хрупких материалов, как указывал А. Смекал [311], прояв­ляется в ослаблении связей меж­ду атомами из-за тепловых коле­баний, действующих во всей тем-

Рис. 5.17. Зависимость приведенной проч­ности (RnP) пеностекла от температуры: 1, 2, — на основе стекла 2Н и антрацита (2На); 3, 4— то же (6На); 5, б —для 6Н и сажи (6Нс)

Пературной области от абсолютного нуля до температуры де­формации? а также в релаксации опасных напряжений вслед­ствие вязкой текучести и поверхностной диффузии, приводящей к закруглению краев микротрещин и уменьшению концентра­ции напряжений у их вершин. Полученная нами зависимость прочности пеностекла от температуры соответствует аналогич­ной зависимости для ряда низкопрочных стекол, которая так­же во всем температурном интервале вплоть до Tg характери­зуется пологой кривой без каких-либо максимумов![312, 313]. Это объясняется тем, что разрывное напряжение стекла на­столько мало, что уменьшение напряжений вблизи микротре - шин проявляется очень слабо. У таких стекол обычно с ростом температуры падает прочность [313].

В изученном нами интервале температуры прочность пено­стекла на сжатие всегда превышает прочность его на изгиб. Поэтому при расчетах, связанных с определением допустимых нагрузок (в том числе термических), необходимо учитывать значение прочности на изгиб.

Полученные нами результаты исследований показали, что прочность образцов пеностекла 6На (рис. 5.17, кривые 3, 4) вы­ше, чем для пеностекла 2На (рис. 5.17, кривые 1,2), а ониже-

Ние ее є ростом температуры соответственно меньшее, что можно объяснить уменьшением количества дефектов в разде­лительных стенках ячеек пеностекла 6На. Для пеностекла на газовой саже (6ИС) эти показатели еще выше (рис. 5.17, кри­вые 5, 6), что связано с повышением качества его структуры.

Зависимость упругих характеристик пеностекла от темпера­туры. Знание упругих характеристик пеностекла представляет большой интерес как с точки зрения его применения, так и в отношении их влияния на термические свойства, учитываемые при разработке режимов отжига.

Упругое поведение всякого изотропного тела характери­зуется модулем продольной упругости Е (модуль Юнга), мо­дулем сдвига G и коэффициентом Пуассона р. Из закона Гука для деформаций в упругой области следует, что величи­ны Е и G показывают пропорциональность между напряже­ниями и деформацией при растяжении и сдвиге, а коэффи­циент р характеризует изменение объема тела при деформа­ции. Эти величины связаны между собой соотношением

\i = —------ 1. (5.15)

2 G к '

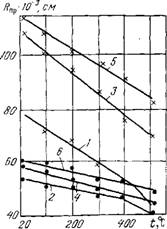
Сведения об упругих характеристиках пеностекла приво­дятся лишь в единичных работах, причем они противоречивы [138, 314]. Поэтому нами в ходе экспериментов было исполь­зовано несколько методов исследований (см. гл. II, пара­граф 3). Для определения упругих характеристик пеностекла при комнатной температуре была использована установка типа ИЧМК. Значения упругих свойств пеностекла при у — = 180 кг/м3 приведены в табл. 25. На рис. 5.18 показана зави­симость E=f(y).

Близкие значения модуля упругости и коэффициента Пуассона были получены тензометрическим методом. Сходи­мость результатов определений подтверждает вывод Г. М. Бартенева [313] о том, что стекла в области до нижней температуры их отжига имеют хорошо выраженную упру­гость, поэтому результаты, полученные с использованием как статических, так и динамических методов, практически совпа­
дают. Анализ их указывает на независимость коэффициента Пуассона от изменений температуры в изученной температур­ной области. Модуль упругости пеностекла (как и у большин­ства силикатных стекол) уменьшается с ростом температуры, что связано, очевидно, с увеличением расстояний между иона­ми в твердой фазе и повышением кинетической энергии тепло­вого движения частиц. Экспериментальные данные, рассчи­танные для пеностекла объемной массой 180 кг/м3, приведены в табл. 26.

Анализ их показывает, что температурные зависимости упругих характеристик пеностекла на основе использованных

Нами составов стекол уменьшаются с повышением температуры, а коэффи­циент Пуассона имеет такое же значе­ние, как и у массивных силикатных сте­кол (ц = 0,18—0,3 [297]). Полученное значение коэффициента Пуассона не-

Рис. 5.18. Зависимость модуля упругости от объемной массы пеностекла, отличающегося характером структуры

Сколько выше значений, приведенных Е. Н. Прокофьевым [314], объясняется это меньшими деформативными способно­стями использованных им образцов пеностекла в связи с их большой объемной массой (у = 300 кг/м3).

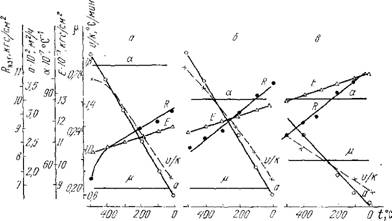
Исследование свойств пеностекла в интервале температур отжига позволяет оценить влияние каждого из этих факторов на безопасную скорость охлаждения изделий из пеностекла и установить общие закономерности, характерные для процес­са отжига. Расчет скорости охлаждения по формуле (5.14) с использованием полученных нами данных при исследовании свойств пеностекла позволил установить новую зависимость температура — скорость охлаждения (рис. 5.19). При выпол-

Нении расчетов толщина блоков (2d) была принята равной 0,1 м при объемной массе пеностекла 180 кг/м3.

Поскольку для определения допустимой скорости охлаж­дения полученные расчетные значения необходимо разделить на коэффициент запаса прочности, то его выбор в значитель­ной мере повлияет на общую продолжительность отжига, осо­бенно если принять его равным 5—10, как принято при отжи­ге массивных стеклянных изделий. Поэтому с учетом прове-

Ренных на практике рекомендаций Ф. Шилла [1] нами был принят К — 3.

Полученные расчетные значения для температурной кри­вой охлаждения пеностекла исключают возможность увеличе­ния скорости охлаждения на заключительных стадиях процес­са отжига, что не согласуется с данными работ [11, 15, 299]. Увеличение скорости охлаждения пеностекла в начальных стадиях процесса охлаждения с последующим ее снижением по мере охлаждения пеностекла косвенно подтверждается ре­зультатами исследований Р. Гар дона [315], который, изучая напряжения в процессе отжига листового стекла, установил рост напряжений при постоянной скорости охлаждения.

Скорость охлаждения в интервале зоны собственно отжига должна быть достаточно низкой, чтобы остаточные напряже­ния, возникающие после ее прохождения, имели небольшие значения. Так как в настоящее время отсутствуют методы, по­зволяющие определить остаточные напряжения, возникшие в

Пеностекле после прохождения начальной зоны отжига, на этом участке можно применять экспериментально установлен­ную рядом исследователей [13, 15] скорость охлаждения 0,6— 0,7 °С/мин.

В отличие от массивных стекол, где за верхнюю темпера­туру отжига принимается значение ее при вязкости стекла 1013 пз (при этом значении ее Tg релаксационный процесс в основном заканчивается в течение нескольких минут), для пеностекла следует принимать более высокое значение тем­пературы, близкое к Гн. д.. При нижней температуре отжига релаксация напряжений длится несколько часов. Значение ее соответствует температуре при вязкости стекла 1014,5 пз.

Таким образом, исходя из предположения, что у алюмомаг- незиального стекла во всей области температур собственно отжига при понижении температуры на каждые 8—10 °С вяз­кость увеличивается в два раза [298], температурный интер­вал для области вязкости 1013—1014'5 пз равен 50 °С и нижняя температура отжига для пеностекла 2Ha(7,g = 510 °С) составит 460 °С, а для пеностекла 6Ha(7'g = 540 °С) — 490 °С.

Анализ данных скорости охлаждения пеностекла в зави­симости от его теплофизических и термомеханических свойств (табл. 27) показывает, что у изученных нами типов пеностек­ла определяющим фактором является температуропровод­ность материала, которая обусловлена степенью и равномер­ностью дисперсности газовой фазы в пеностекле. Термомеха­нические характеристики оказывают незначительное влияние на скорость отжига данных типов пеностекла, поскольку ме­ханическая прочность и модуль упругости, связанные обратной зависимостью, характеризуются изменением своей абсолютной величины от температуры в зависимости, близкой к постоян­ной величине, а коэффициенты термического расширения пеностекла 2На и 6На мало различаются между собой. При отжиге пеностекла 6Не с улучшенными структурно-механиче­скими показателями необходим более длительный режим от­жига, причем зависимость температура — время отжига при­ближается к линейной, в то время как кривая отжига пено­стекла, вспененного на основе антрацита, соответствует кривым, характеризующим инерционный тип отжига.

При наличии в структуре пеностекла сообщающихся кана­лов между отдельными ячейками температуропроводность его значительно повышается, что позволяет вести более ускорен­ное охлаждение его на протяжении всего периода отжига.

Математический анализ рассчитанной нами зависимости температура — скорость охлаждения (табл. 27) показывает, что она соответствует кривым, характеризующим инерцион­ный тип отжига [298], и может быть описана уравнением t— ( — Се~Кх (5.19), где t — температура в момент времени т; т —

Время от начала охлаждения; С и К—постоянные, завися­щие от свойств пеностекла.

Установленная экспериментально зависимость темпера­тура— время отжига подтверждается выполненными В. Л. Инденбомом и Л. И. Видро [316] расчетами, согласно которым замедляющее в зоне температур отжига охлаждение оказывается для получения минимальных структурных и тер­мопластических напряжений более выгодным, чем принятое обычно равномерное или ускоряющееся охлаждение.

Исследование свойств пеностекла и процессов, протекаю­щих в нем в интервале температур отжига, позволяет заклю­чить следующее.

Термомеханические свойства пеностекла зависят от харак­тера его структуры. Так, пеностекло на основе стекла 6Н,

Г

Обладающего меньшей склонностью к кристаллизации, обла­дает более высокими прочностными показателями, чем пено­стекло на основе стекла 2Н.

Термомеханические свойства пеностекла подчиняются за­кономерностям, тождественным для низкопрочных силикатных стекол.

Одним из основных факторов, влияющих на скорость охла­ждения изученных видов пеностекла, является его температу­ропроводность. Расчеты показывают, что практически безо­пасная скорость охлаждения пеностекла в начале процесса может быть равной 1,2—1,8°С/мин, снижаясь в конце его до 0,6—0,7 °Cj мин.

Постоянство свойств пеностекла зависит от скорости его от­жига и наличия дефектов структуры, обусловленных видом ис­пользуемого газообразователя и склонностью стекла к кри­сталлизации.

Температурная кривая отжига должна рассчитываться на основании данных значений термомеханических и теплофизи- ческих свойств пеностекла, находящихся во взаимосвязи с данными свойств исходного стекла и структурой пеностекла. Для этой цели может быть использована известная формула А. Н. Даувальтера, рекомендованная им для расчета скорости отжига монолитных стекол.

Величина коэффициента запаса прочности (К), учитывае­мая при расчете скорости отжига, выбирается с учетом дила­тометрических и прочностных характеристик пеностекла и на­ходится в пределах 2—4. Для изделий одного вида большее значение К принимается в случае более мелкопористого пено­стекла с замкнутой структурой.