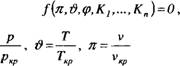Однокомпонентные рабочие вещества
Термодинамические свойства
Термодинамическими параметрами любого рабочего вещества являются:
• давление;
• температура;
К термодинамическим свойствам рабочего вещества относят:
• удельный объем;
• удельное тепло фазового перехода;
• теплоемкость;
• показатель адиабаты;
• энтальпию;
• энтропию.
Расчет термодинамического цикла холодильной машины (теплового насоса, теплофикационной машины) подразумевает определение термодинамических параметров рабочего вещества в узловых точках цикла. В большинстве случаев заданными являются только две характеристики (например, Т и р, р и s и т. д.), что является достаточным для од покомпонентных рабочих веществ. Остальные термодинамические характеристики могут быть определены через соответствующие уравнения.
|
(6.1) |
Для определения всех термодинамических свойств рабочего вещества используют термодинамические диаграммы состояний рабочих веществ (глава 2), таблицы или компьютерные программы расчетов. В основе создания перечисленных источников получения информации всегда лежит система уравнений, связывающая все термодинамические параметры и свойства рабочего вещества. В качестве примера рассмотрим некоторые основные уравнения. Уравнение Менделеева-Клапейрона
Р v - RT
Оказывается «неработоспособным» для области влажного пара и слабо перегретого пара, однако именно в этих областях и требуется определение термодинамических свойств рабочих веществ для паро - компрессорных холодильных машин и тепловых насосов.
|
(6.2) |
Использование уравнения Дюпре для реальных газов
Р (v-b) ~ R T
и уравнения Ван-дер-Ваальса
P + ~j{v~b)=RT (6.3)
Дает недостаточную точность для инженерных расчетов (а и Ъ - коэффициенты, определяемые экспериментально для каждого рабо - чеего вещества). Более точным является уравнение Битти-Бриджмена, однако многие авторы указывают на определенные сложности при его практическом использовании
>= 2 '(V + Д)—Т
V v
Где є - коэффициент.
В последнее время предпочтение отдается расчетам по двух - константному уравнению 3-го порядка Пенг-Робинсона, которое позволяет описывать термодинамические свойства рабочих веществ с достаточной для инженерных расчетов точностью как в области пара, так и в области жидкости. Кроме того, это уравнение достаточно легко решается в аналитическом виде, что существенно ускоряет процедуру расчета термодинамических свойств с использованием ЭВМ. Для расчетов необходима следующая информация: критическое давление (ркр) рабочего вещества и его критическая температура (Ткр), а также фактор ацентричности Питцера и идеальногазовая теплоемкость. Уравнение Пенг-Робинсона используют для расчета свойств рабочих веществ HFC - и HCFC-типа, а также компонентов воздуха
P=IL------------------ *П------------ . (6.5)
V-b v(v + b) + b(v-b)
Введя комплексы А = —, В = и Z =-------------------------------------- , получаем
R2T2 RT RT
Уравнение 3-го порядка
Z3 -(1-В )Z2 +(А-ЗВ2 -2B)Z-(AB-B2 - В3 ) = 0. Величины, входящие в уравнение Пенг-Робинсона:
NZCRT«P
|
|
Параметр b = р-------------------------
'кр
Где + и z =-±- = 0,307401308 ;
3 3 3е з+р
• параметр а(Т) = а^с,
VV(5P2 +6fi + 3)RT« I,
Где а = —--------------------------------- — и at = U + m(l-
Видно, что все уравнения для расчета термодинамических свойств рабочих веществ, сводятся к уравнению Менделеева - Клапейрона, различие составляют введенные коэффициенты, параметры и поправки, определяемые экспериментально.
Для расчета других термодинамических свойств рабочего вещества используют эмпирические выражения (процесс совершенствования которых не прекращается и поныне) как функции: параметров в критической точке (ркр, Ткр и Vjcp), нормальной температура кипения Ts, нормального удельного тепла фазового перехода rs и молекулярной массы fi.
Некоторые из этих параметров входят в безразмерные критерии подобия, наиболее известными из которых являются: • число Трутона
Mrs.
Т ls
Число Гульдберга
(6.7)
Т
Синтез новых рабочих веществ должен носить направленный характер, т. е. по желаемым свойствам рабочего вещества необходимо найти его химический состав. В последние годы синтез новых рабочих веществ идет по пути создания экологически чистых рабочих веществ как альтернативы тем, которые должны быть изъяты из употребления. По этому принципу в 1990-ые годы был синтезирован R-134a как основанная альтернатива R-12.
Располагая данными хорошо изученного рабочего вещества, возможно определять свойства неисследованного вещества, если совпадают безразмерные критерии этих двух веществ. В этом случае универсальную функцию свойств рабочего вещества записывают в виде
|
|
|
Где п = |
|
, К} ... Кп~ вспомогательные критерии |
(более 20), которые помогают увеличить степень точности при описании свойств неисследованного рабочего вещества. Использование большого числа вспомогательных критериев превращает задачу синтеза новых рабочих веществ в самостоятельную область исследований, зачастую весьма далекую от практических задач выбора рабочего вещества для холодильных машин и тепловых насосов, в связи с чем пропадает интерес к детальному рассмотрению этих разработок. Кроме того, предлагать к использованию недавно синтезированное рабочее вещество нецелесообразно, пока не будут достоверно известны его конструктивно-эксплуатационные свойства.
Отметим огромный вклад, внесенный И. И.Левиным, И. С.Бадылькесом и Л. М.Розенфельдом в становление и развитие отечественной школы по изучению свойств рабочих веществ холодильных машин и тепловых насосов. В мире широко известны результаты современных исследований и созданных на их основе многочисленных пакетов прикладных программ, выполненных в научных школах, возглавляемых Х. Крузе (Германия) и К. Ватанабэ (Япония). Значительный вклад в развитие этого направления в науке сделан научными группами при крупных мировых производителях синтезированных рабочих веществ.
Рассмотрим влияние химического состава рабочих веществ на их термодинамические свойства.
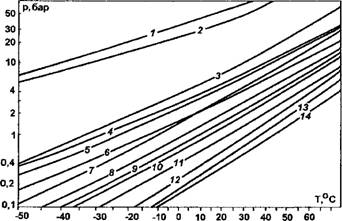
Точки кривой p~f(T) характеризуют состояния, в которых возможно термодинамическое равновесие между жидкостью и насыщенным паром. Эта кривая называется кривой фазового равновесия, она имеет ограниченную протяженность и заканчивается в критической точке. При анализе уравнения p—f(T) в координатах lg р-~
Получают почти прямолинейную зависимость (рис.6.2). Эта особенность отражена при создании диаграмм состояний рабочих веществ
|
Рис.6.2. Зависимость между давлением и температурой кипения различных рабочих веществ: 1 - R-744 (С02); 2 - R-170 (С2Н6); 3 - R-717 (NH3); 4 - R-12; 5 - R-40; 6 - С4Н10; 7 - S02; 8 - R-114; 9-R-2I; 10-R-160; ll-R-41; 12-R-611; 13-R-30; 14-R-150a |
Fe Р ~ ~ •> которые для однокомпонентных рабочих веществ
Практически никогда не применяются, однако широко используются для смесей рабочих веществ, особенно «агент-сорбент».
Нормальная температура кипения Ts всех рабочих веществ HFC - и HCFC-типа достаточно точно определяется на основании эмпирического выражения
Ts = 6,875z -0fi625zm-101,23т + 12,5т2 -30,75 (6.9)
Где т - число атомов Н; z - число атомов F и/или С1.
Удельный объем пара рабочего вещества определяется на основании одного из уравнений состояний - ур.(6.2)-(6.5).
Удельное тепло фазового перехода г является функцией химического состава рабочего вещества, следовательно, и его молекулярной массы Известно, что высокомолекулярным рабочим веществам соответствуют меньшие значения г. Кроме того, вдали от критической точки величина г мало зависит от температуры.
Для расчета величины г используют уравнение Тизена
Или его модификацию
|
П |
|
Т |
|
|
|
1- |
|
Кр |
(6.106)
Где а, п~ коэффициенты (например, а=8,83 для R-22 и п~3/8 для всех рабочих веществ HFC - и HCFC-типа метанового ряда).
Теплоемкость* для рабочих веществ в широком интервале изменения температур должна быть определена для трех состояний: твердое вещество, жидкость и пар.
Особый интерес для холодильных машин и тепловых насосов представляет анализ величины теплоемкости рабочего вещества. Теплоемкость может быть графически определена в диаграмме состояний T-s как проекция длины подкасательной, проведенной к соответствующей изобаре или изохоре при заданной температуре. На рис.6.3 приведен пример графического определения изобарной ср и изохорной cv теплоемкости (еще раз можно убедиться в справедливости неравенства cp>cv). Отметим, что теплоемкость насыщенной жидкости и перегретого пара всегда является величиной положительной, в то время как теплоемкость насыщенного пара может принимать как положительные, так и отрицательные значения в зависимости от* формы пограничной кривой рабочего вещества, т. е. его термодинамических свойств. Использование рабочих веществ, которым соответствует положительная величина теплоемкости насыщенного пара, связано с ограничениями, накладываемыми на безопасность эксплуатации компрессора. При всасывании даже перегретого пара процесс сжатия проходит в области влажного пара, что может явиться причиной гидравлического удара в поршневом компрессоре (рис.5.8в).
|
(6.11) |
Показатель адиабаты для реального рабочего вещества определяется как
Jfc=Jfc"d-ane +Ak
Л и д. газа Q
Где кид'газа = —----- , а корректирующий член Ак учитывает влияние
Си. газа
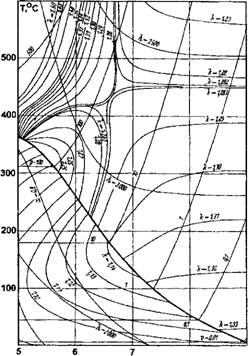
|
Рис.6.4. Диаграмма состояний Т-s для воды с линиями к.—const вблизи правой пограничной кривой |
|
8 5,кДж/кгК |
Температуры на изменение свойств реального рабочего вещества. На рис.6.4 приведена диаграмма T-s для воды, на которую нанесены линии k-const. Для рабочих веществ холодильных машин и тепловых насосов линии k=const на диаграммах состояний отсутствуют ввиду незначительного изменения этой величины в диапазоне работы парокомпрессорных холодильных машин и тепловых насосов, поэтому в инженерных расчетах используют некоторое усредненное значение, например, к - 1,3 для R-717; к - 1,08 ... 1,2 для большинства рабочих веществ HFC - и HCFC-типа. Графическая интерпретация величины к - угол наклона изобар в области перегретого пара в диаграмме T-s и угол наклона адиабат в области перегретого пара в диаграмме lgp-h.
|
|
|
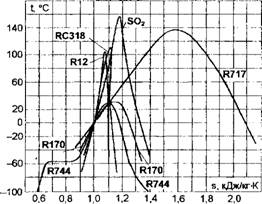
Рис.6.5. Изображение пограничных кривых в диаграмме T-s для некоторых рабочих веществ |
Определение энтальпии и энтропии проводится по известным термодинамическим уравнениям (глава 2), в которые, как и ранее, вводятся инженерные упрощения и уточняющие эмпирические зависимости, описывающие особенности реальных рабочих веществ.
Совмещенное изображение кривых насыщения для различных рабочих веществ представлено на рис.6.5. Видно, что для определенного режима работы холодильной машины (теплового насоса) можно выбрать множество рабочих веществ, однако различными являются их термодинамические свойства, следовательно, будут отличаться термодинамические и термоэкономические характеристики одного и того же схемного решения холодильной машины (теплового насоса), использующего различные рабочие вещества.
Таким образом особый интерес представляет анализ термодинамических свойств рабочих веществ в контексте их оптимального выбора для реальных условий эксплуатации, что будет показано далее.