Обратимые циклы
Для того, чтобы непрерывно получать полезную работу необходимо располагать двумя источниками тепла (тепловыми резервуарами) с разными температурами, между которыми рабочее вещество совершало бы в тепловой машине многократно повторяющийся круговой процесс - термодинамический цикл.
Поскольку низшей температурой в прямом термодинамической цикле обычно является температура окружающей среды, то величина Тср стала традиционным множителем в уравнении Гюи-Стодолы. Ур. (2.21) в виде A W~Tcp AScucm не всегда возможно убедительно доказать (как для прямых, так и для обратных термодинамических циклов), если Тср не является одной из изотерм, на которых построен цикл.
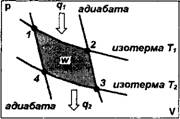
В случае, когда оба источника тепла имеют постоянные температуры, наилучшей комбинацией процессов, составляющих цикл, цель которого состоит в получении максимальной работы, являются два изотермических и два адиабатных. Таким образом мы подошли к рассмотрению цикла Карно.
Абсолютная величина работы, полученной в тепловой машине за один цикл работы, согласно Первому закону термодинамики, определяется как
W=QJ-Q2, (2.22)
Где Qі - тепло, отданное высокотемпературным источником тепла рабочему веществу; Q2 - тепло, отданное рабочим веществом низкотемпературному источнику тепла.
Количественная характеристика процессов преобразования тепла и работы в цикле описывается величиной СОР (англ. - coefficient of performance - коэффициент преобразования). Логическое выражение для определения величины СОР справедливо для всех типов энергопреобразующих систем
Полезный энергетический эффект
СОР =------------------------------------------------------ . (2.2j)
Затраченная энергия
Выражение для СОР основано на Первом законе термодинамики. В литературе прошлых лет изданий величина СОР для тепловых (энергетических) машин называлась тепловым коэффициентом и обозначалась? f, что иногда вводило в заблуждение, так как эта же обозначение использовалось для описания КПД (ур. (2.11)).
Коэффициент преобразования тепловой машины равен
= = (2.24)
ИЛИ
В современной технической литературе можно найти обозначение СОР с любым нижним индексом, обозначающим тепловую машину (например, СОРпряМшЦикла> или английское обозначение COPdirect). Аналогично претерпели изменения и традиционные обозначения для машин, работающих по обратным термодинамическим циклам, что будет рассмотрено в главе 3.
Рис.2.2. Прямой цикл Карно (для тепловой машины)
СОРТМ=1-^- = 1-^-. (2.25)
У/ h
|
(2.26) |
|
(2.29) |
|
Ті J |
|
Wmax ^Ql |
|
Где знак «=» соответствует идеальной тепловой машине (произведенная работа будет максимальной), знак «<» соответствует тепловой машине, в которой имеют место необратимости. |
Величина СОРтм, рассчитанная по ур. (2.25), представляет максимальное значение СОРтм, которое соответствует тепловой машине, работающей между источниками тепла с Tj=const и T2=const. Из ур.(2.18) для обратимого цикла Карно следует
Или с учетом знаков
Оі_+®2- = 0, (2.27) Т, Т2
Тогда для необратимого цикла
Tj Т2
|
|
Таким образом можно записать выражение для определения работы, произведенной в тепловой машине
Изложенные соотношения по определению коэффициента преобразования цикла Карно обобщаются двумя теоремами Карно: Теорема 1. СОРКарно не зависит от природы рабочего вещества и расположения предельных адиабат цикла, а определяется только температурами источников тепла.
СОРтах любого обратимого цикла в заданном интервале температур равняется СОРКарно в том же интервале температур. Теорема 2. СОР необратимого цикла всегда меньше СОР обратимого цикла в том же интервале температур.
Теоремы Карно указывают пути повышения СОР тепловых машин; они сыграли основную роль в развитии теоретических основ теплотехники и теплоэнергетики. Несмотря на то, что ни одна из применяемых на практике тепловых машин не работает по циклу Карно, величина СОР этого цикла имеет максимальное значение по сравнению с СОР других циклов, работающими в тех же температурных границах и является мерой для сравнения циклов. Обе теоремы являются следствием Второго закона термодинамики и совместно могут рассматриваться как одна из его формулировок.
Наряду с циклом Карно существует целый ряд обратимых циклов, которые осуществляются между двумя источниками тепла. Подвод и отвод тепла в них происходит изотермически; что касается двух других процессов, то они в диаграмме «Т-s» представлены двумя произвольными, но эквидистантными линиями (таблица 2.1).
Используя диаграмму «Т-s», приведем доказательство равенства между собой СОР всех обратимых циклов с двумя постоянными температурными уровнями источников тепла (рис.2.3). Эти циклы носят общее название - обобщенный цикл Карно.
Предположим, что ABCD - обобщенный цикл Карно. ВС и AD - две изотермы, а АВ и CD - две эквидистантные линии.
Рабочее вещество, начиная цикл из точки В, расширяется изотермически по линии ВС, получая от высокотемпературного источника Ті некоторое количество тепла qr, затем происходит изменение состояний по CD. В соответствии с изображением цикла, в процессе CD энтропия уменьшается. Следовательно, рабочее вещество должно отдавать тепло в количестве, эквивалентном wi.(C-Ds3-s4). Для того чтобы цикл был обратимым, тепло должно быть отдано при температурах, равных температуре рабочего вещества. Так как эта температура все время изменяется, то между С и D необходимо было бы расположить бесконечный ряд источников
Тепла, которые воспринимали бы от рабочего вещества тепло при температурах рабочего вещества.
После прохождения мимо этого ряда источников, рабочее вещество отдает тепло низшему источнику по изотерме AD. Из точки А рабочее вещество должно пройти по кривой АВ и получить тепло, эквивалентов m.(A-B-S2-S]). Это тепло может быть воспринято из того же ряда источников тепла, который был установлен по линии CD. Вследствие эквидистантности кривых АВ и CD каждый из промежуточных источников тепла отдаст рабочему веществу столько теплоты, сколько получил ранее при изменении состояния рабочего вещества по CD. Таким образом, баланс каждого источника тепла за цикл будет равен нулю. Следовательно, эти промежуточные источники тепла не обладают свойствами источников тепла в традиционном смысле (из которых все время черпается или которым все время отдается тепло). Достаточно предположить, что
|
Таблица 2.1
|
Они обладают способностью сохранять тепло в течение цикла, т. е. их можно назвать термостатами или аккумуляторами тепла.
В любом обобщенном цикле Карно источники тепла Т} и Т2 остаются постоянными (аналогично циклу Карно). Эквидистантность процессов АВ' и CjD, а также АВ" и C"D обеспечивается условием равенства изменения энтропии в процессах AS=ASAd-A$bc, AS=AS=AS" соответственно.
Все вышеприведенное является справедливым как для анализа прямых, так и обратных термодинамических циклов.
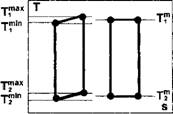
Существуют еще два обратимых термодинамических цикла. Они состоят из двух адиабат и двух эквидистантных линий, по которым происходит процесс подвода и отвода тепла в цикле. В общем случае Theorist и T^const. Такой цикл носит название цикла Лоренца, а его частный случай - две адиабаты и две изобары (Тіфсотї и Theorist, но pi-const и р2—const) - цикла Джоуля (рис. 2.4). При анализе этих циклов можно представить, что процесс подвода и отвода тепла осуществляется при помощи непрерывного ряда тепловых резервуаров с постоянными температурами. При этом из каждого резервуара система поглощает бесконечно малые количества тепла SQ. В этом случае ур.(2.18) принимает вид
J(2.30)
И широко известно как интеграл Клаузиуса. Здесь, как и прежде, знак «=» относится к обратимым циклам, а знак «<» - к необратимым.
|
А) б) Рис.2.4. Обратимые циклы с переменными температурами подвода-отвода тепла: а) Лоренца (Джоуля); б) эквивалентный цикл Карно |
Цикл Лоренца (прямой и обратный) и его частный случай - цикл Джоуля (прямой и обратный) могут быть для упрощения заменены эквивалентным циклом Карно, т. е. циклом Карно, в котором источниками тепла будут некоторые средние температуры: ТГ между ТГ™ и ТГ а Т2т между Т2тах и Т2тіп (рис.2.4).
Значения ТУ" могут быть рассчитаны двумя способами:
• для цикла Джоуля как среднеарифметические
Rp max, >j, min
• для цикла Лоренца как среднеэнтропийные
Тал
J TkdS
К гт max г» min ^к ^ к
В результате рассмотрения всех обратимых циклов можно сделать выводы:
• СОР любого обратимого цикла не зависит от свойств рабочего вещества;
• СОР всех обратимых обобщенных циклов Карно, осуществляемых между постоянными температурами Tj и Т2, равны;
|
(2.33) |
|
С = |
|
'«1 dT ) |
• для проведения анализа любой цикл может быть заменен эквивалентным циклом Карно.