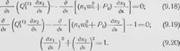Механика трубопроводов и шлангов

Уравнения равновесия шлангов

Векторные уравнения равновесия шланга. На рис. 9.1 пока­зан шланг, по которому движется жидкость. Шланг, как прави­ло, обладает малыми жесткостями на изгиб и кручение, что су­щественно осложняет решение задачи статики, так как из-за ма­лой жесткости под действием внешних сил шланг может очень сильно изменять свою форму. Поэтому приходится рассматри­вать в общем случае нелинейные уравнения равновесия, для ко­торых получить решение в аналитической форме, как правило, не удается. В реальных условиях при больших длинах шланга (по сравнению с диаметром поперечного сечения) жесткостью шланга можно пренебречь, что при расчетах приводит к модели абсолютно гибкого стержня. Следует иметь в виду, что эта мо­дель является предельным случаем. Решение, соответствующее предельному случаю, можно уточнить учитывая реальные же костные характеристики шланга, по это приводит к резкому усложнению уравнений равновесия, так как жесткий шланг ни­чем не отличается от гибко­го стержня. Более подробно об этих уравнениях и их приближенных методах ре­шения будет сказано в по­следующих пунктах данного параграфа.

Рассмотрим вначале пре­дельный случай, когда шланг можно рассматривать как абсолютно гибкий стер­жень (нить). Б этом пре­дельном случае Ац=0 (г= 1,

2, 3), а вектор равен

Ё=(3‘,1)ё1, (9.1)

------ — [(таВДо+Р^ё^ + ^+^О. (9.2)

&Ч С>&‘

Если на шланг действуют сосредоточенные силы (см. рис. 9.1) 1% (у=1,..., /г), то уравнение (9.2) примет вид

----- £- Кт. М: + Р, У,] Йй+У+^]Р(>)8^-*,) = 0.

(9.3)

Переходя к безразмерной форме записи, полагая нилучим рй=(&11)1а., где ()— безразмерная

Осевая сила.

--- £- [(я,^+Р1Й,1 + ?Ч V р(-)8(г-в,)=0, (9.4)

Где Р0=Ро/ (т 1 + т2) #/.

В дальнейшем значок тильды над безразмерными величина­ми опускается. Безразмерная погонная сила тяжести

=— ъ^,. (9.5)

Под действием сосредоточенных сил Р(у) осевая линия шлан­га станет пространственной кривой. Перемещения точек осевой танин шланга между точками приложения сосредоточенных сил определяются из уравнения (5.21):

TOC o "1-5" h z ~ +(/„- 1)ё1+4ё2+41ёз=-0. (9.6)

Уравнение равновесия шланга (9.4) можно представить и в иной форме записи, объединив первые два слагаемых:

Ь?„+^+У]р<->8(Е-О = 0, (9.7)

Где =$1) — п-ри о — Ри. (9.8)

При решении уравнений равновесия шланга, нагруженного сосредоточенными силами, следует иметь в виду, что в точках приложения сосредоточенных сил должны выполняться локаль­ные уравнения равновесия:

7^>+Р, К_0)+й К+11)=0, (9.9)

Где (^(е^о) — натяжение в сечениях шланга, прилегающих к се­чению, где приложена сила Ру При стыковке участков шланга

63

В местах приложения сосредоточенных снл первая производная вектора перемещения а з этих сечениях разрывна.

Уравнение (9.7) тождественно совпадает с уравнением рав­новесия шланга без учета потока, т. е. (21 — это осевое усилие в шланге, вызванное только внешними силами, которые можно определить из уравнения (9.7). Усилие в шланге <2Т с учетом по­тока жидкости находится из соотношения

Ч^^г+п^+Р,,. (9.10)

Вторая особенность задач статики шлангов заключается в том (это следует из уравнения (9.7)), что поток жидкости пе из­меняет форму шланга, которую он получает при Шо=£>о=0 под действием внешних распределенных сил (при, РГг,>=0).

Уравнения равновесия^ шланга в проекциях на неподвижные оси. Представим вектор @1 через проекции иа оси Хг (опуская значок тильды над безразмерными величинами):

О*}, - тг) • (9- и>

Аналогичным образом можно представить и вектор

(и.,®20+ Р0) «! = ]£] («1™»+1- (9.12)

В результате получим следующие уравнения равновесия шланга (при до=0 и 7=—^2г)'-

+ 2яЦ>8(е-е,)=° (9.13)

Или

~у£ - (о, - «2,- -1 - ] (е - Е„)=:0 (г-= 1, 2, 3). (9.14)

Дополнительно к системе уравнений (9.14) имеем соотно­

Шение

±т=>- ^

При стационарном движении идеальной жидкости выполня­ется уравнение Бернулли (в безразмерной форме)

Где постоянная с находится из краевых условий для потока жидкости. Например, считая, что «входом» является точка О (рис. 9.1), получим

(9.17)

В результате получаем систему из пяти уравнений (9.14) —

(9.15) с пятью неизвестными: х, х% *з» и Ро.

Частный случай уравнения равновесия шланга в неподвиж­ных осях получим, когда рм=0. В этом случае под действием сил тяжести форма осевой линии шланга есть плоская кривая, расположенная в плоскости хОх^. Уравнения равновесия имеют вид

При интегрировании системы (9.18) — (9.20) удобнее урав­нения представить в форме

(9.21)

Интегрируя уравнения (9.21), получаем [60]

(9.22)

(9.23)

Интегрируя (9.23), имеем

(9.24)

Так как

То с учетом соотношения (9.24) при *ю=0 получим

(9.26)

Исключая из (9.24) х [используя соотношение (9 26)] нахо­дим Х21

Х2=с11 -}-^ -[- г3 (сз=Сі эИ с2). (9.27)

Из (9.26) следует

_!Ё!_ =---------------------- !-------- (9.28)

*

Воспользовавшись (9.28), из (9.22) находим

Сі=С! сЬ (^г~ + сг1 ■ (9-а9)

Уравнения (9.30), (9.33) и (9.34) позволяют последователь­но определить все три постоянные. Для проверки правильности найденных частных значений постоянных можно использовать уравнение

С3—х2к — Сі сЬ —- с2^.

Решение уравнений равновесия шланга можно получить и в параметрической форме (в зависимости от е), что более удобно при расчетах. Интегрируя второе уравнение системы (9.21), получаем

С,—:=6 + 4°. (9.35)

Исключив ИЗ полученного соотношения <21, имеем

„хг _ « + 41»

Полагая е=0, находим Сз(1) через ранее введенные постоян-

М ю:

С[1*=с1 бЬг2- (9.37)

Возведя выражения (9.22) к (9.35) в квадрат и сложив их, получим

Гак как произвольные постоянные С и входящие В фь опре­деляются из краевых условий, что произвольные постоянные в

(9.40) равны нулю.

Так как — (^о-Ья^с), а Рс определяется из урав­

Нения Бернулли (9.16):

Ро=ро0~ «Л то безразмерное натяжение в шланге

С?1 } (£) = ^1 00 — «1*2 + Рио + «Ї^О-

=0, плотность р2=103 кг/м3. При этих значениях получаем f», =

=2,36 кг/м; m2= P--i~ 1.96 кг/м При этих числовых значениях парамет­

Ров система безразмерные величины

П, =———- =0,454; Р,, и,182; то0 = 0,4.

/«1 + ГП‘2

Подставив в (9.42) числовые значения постоянных слагаемых, получим С(11)= Qi — 0,454дг2(б)Н 0,182 + 0,073,

Где ГО0=0,182; n, iЈJo2=0,073,

Значения х2(е) для ряда 6 следующие:

Е. . . 0 0,2 0,4 0.5 0,8 1

Хя. .0 —0,099 -0,086 0,028 Р, 185 0,4

График изменения натяжения в шланге с учетом потока QiiIf показан на рис. 9.2. Поток жидкости существенно изменяет натяжение в шланге, что необхо­димо учитывать как при расчете на прочность, так и при определении частот­ных характеристик шланга с текущей жидкостью.

Уравнения равновесия шланга в проекциях на связанные оси. Переходя к локальным производным в уравнении (9.7), получим

^-i1 + xx(Q1-el)+?„ + Y+^P'”>8(e-O = 0; (9.43)

В проекциях на оси базиса {е*}

-fL+?, + V. + ^PS”)S(^-olo; (9.44)

<мЛ‘ь-’2+2 (Е - ^0; (9-45)

«=1

УН?.!+^Рз,)б('- ^)=-а (9.46)

Из (9.46) следует

Уравнения равновесия шланга с учетом изгиб ной жесткости.

Рассмотрим частный случай, когда шланг нагружен только си­лами тяжести. В этом случае форма осевой линии шланга есть плоская кривая. С учетом изгибной жесткости внутреннее уси­лие в шланге

+ (01=01° — («1^0+Яи)); (9.47)

В проекциях на неподвижные оси

И«.

Так как с учетом изгибной жесткости уравнения равновесия шланга совпадают с уравнениями равновесия трубопровода, то в проекциях на неподвижные оси получаем (в безразмерной форме)

1 = 0; (9.49)

Дг |_ ди де J

= (9.50)

Дополнительно имеем уравнения

<9-53>

В уравнения (9.49) — (9.52) входят безразмерные СМ1), ($2, Мз, х3 и Лзз, равные

(2г=(£.1{тх т2) т2) gl, Л /3 = МзЦт1 -- т2) ф;

Л33= А%1{тх -(- ^г) 8Р хз=*&

(индексом нуль обозначены размеримте - величины).

Остальные безразмерные величины совпадают с ранее вве- ■генными. При малой изгибной жесткости использовать Л33 при приведении к безразмерной форме внутренних усилий нельзя, 1лк как при Л33—>-0 <Зг и М* стремятся к бесконечности, т. е. нель­зя получить предельный случай, когда Л33=0. Система из пяти уравнений (9.49) — (9.53) содержит пять неизвестных: фь (?2, М3, хх и лг2.

Считая Л зз малым параметром, получим алгоритм прибли­женного решения системы уравнений (9.49) — (9 53), полагая

@1—Ф1э+1аФи-|-1а2,312-ЬУ'3Фп —^лз)» (9.54)

^2 = К‘С?21-|_ И’2Р22-(-К,3С?2зН- ■■■» (9.55)

М3=м31 + М*за+^33+ • ■ (9.56)

•^1=*10-{_1а'^11-Ь1а2'^12-1-!а3-^1з_{_ ■■■’ (9.57)

*^2==*^20 ~1^21 ~!а^*22—|~ Ь^-^23» (9.58)

Где хц удовлетворяют однородным краевым условиям.

= (9.59)

Из системы (9.49) — (9.53) получаем систему уравнений пер­вого приближения:

-fls.fw. f-«.!*]-«;

(9.Щ)

Улц] илц . ил-2{) ил-21 _ 0

~е дГ' & дё~~

В системе (9.60) неизвестными функциями ЯВЛЯЮТСЯ Фи, С}21 у

М3„ *11 II Х21.

Система уравиеинй второго приближения имеет вид —~4^12*10— ^21-^21 ^22-^20] =0;

—-— [010^22 ~~ (^цХ21 “Г Ql2x^ — — ($22х1о] “

-!^=-д22; (9.61)

08

[^10^21 —)--Х20' Хц Х'21)'Хц Хю-Хл] •

XI1 --2Х]0‘Х12--Х21 2x20^22=0.

Системы уравнений (9.60) и (9.61) н последующих прибли­жений являются линейными, что позволяет использовать для их решения хорошо разработанные численные методы, например методы прогонки.