Механика трубопроводов и шлангов

Определение частот и форм колебаний прямолинейного шланга при стационарном потоке идеальной жидкости

'Рассмотрим вначале наиболее простой случай — прямолиней­ный шланг (рис. 31.1) [77]. Уравнение малых колебаний прямо­линейного шланга является частным случаем уравнений (30.33), имеет вид

(31.1)

Определение частот. Решение уравнения (31.1) ищем в виде

Щ=и0 (Е)е'Р'.

В результате получаем уравнение относительно

(31.3)

Тде

А2=——; <У10=С10) — Ро~ «1®о.

(?ю

Входящее в (31.4) натяжение равно статическому иатя* .жению, не зависящему от потока жидкости. В свою очередь, ре­шение уравнения (31.3) ищем в виде

Что приводит к характеристическому уравнению

£2—Ау1к--а2—0, (31.6)

Корни которого

Ш,±У — а^-4а2 ( а, ±1 о?+4а2

*ь»=------------- Т-------------- =*(--------------- 5------------ ). (31.7)'

Общее решение уравнения (31.3) имеет вид

Ио=с^1В--с^лЯ. (31.8)

Решение (31.8) должно удовлетворять однородным краевым

Условиям, что приводит к следующим условиям:

0=1 1 4 = 0 (31.9)

Е<ь-ь)=1. (31.10)

А1-А2=2 АЩ (31.11)

Или

3}/а?-|-4а2=2лл. (31.12)

Из (31.12) находим

===-. (31.13)

Г С? ю + 0^

Подставив в (31.13) выражения для <2ю, и выполнив преобра­зования, получим

ЯП (фШ — Р0 — п^1)

Р"=1~ ,-г; = 2 2- (31Л41

V ОЦ’-.Ро-С'Ч-яЙЧ'о

Из выражения для частот (31.14) как частный случай (при - «1=1 и Ро=0) получаются частоты колебаний движущейся стру­ны. Имеются две критические скорости движения жидкости, при которых частоты становятся равными нулю и бесконечности. Эти критические скорости соответственно находятся из условий

С® — Р0 — /г1®о*=0; (31.15)

<2о - р0 - (я, - пЬ о&.=0. (31.16)

Из выражений (31.15) и (31.16) следует, что критическая

Скорость Шс**, при которой частоты обращаются в бесконечность.

Больше критической скорости w0* (так как Значение

Скорости Wo», при которой часто­ты становятся равными нулю, эк­вивалентно потерн статической устойчивости, поэтому реализо­вать второй критический случай в реальных системах практичес­ки невозможно

Определение форм колебаний шланга с движущейся жидко - 0 стью. Определив частоты, нахо­дим корни характеристического уравнения:

+ *V2n)» (31.17) р„с 3f.2

Где У 2п = ЯП. (31.18)

Так как при е=0 «о=0, то произвольные постоянные cv и с? связаны соотношением

(31.19)

Поэтому собственные функции (полагая ш = 1)

<prt (е) ===== е 1 —е 2 . (31.20)

После преобразований получаем следующее выражение для собственных функций:

Ср„(б)=2 sin *Vme sin y2rfi “ cos ylne • sin y2ns> (31.21)

Т. e. собственные функции являются комплексными функциями вида

Cpn=cpi„ 4- /ср2и. (31.22)

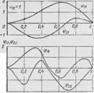
На рис. 31.2 приведены графики действительной и мнимой частей функций фп для двух первых частот при следующих про­извольных значениях: Qio(1)=4; Ро—2; пi =0,8; ^0=0,5. При

Z<Do—'0 получаем формы свободных колебаний струны. Функции фn (F) удовлетворяют уравнению

- Ъ&ёа. ^+а2,ср(1=0 = (31.23)

Qio ■' vio

Получим условие ортогональности, которому удовлетворяют функции фп. Уравнение (31.23) можно представить в виде

Собственная функция с индексом £ удовлетворяет аналогич­ному уравнению:

-^]+^-'“1,‘Ч=о. (31.25)

Умножив уравнение (31.24) на а уравнение (31.25)

На и вычитая получающиеся уравнения, имеем

— (а2к - Я2в)<РЛе_‘(‘,1"+“1,‘>'=0. (31.26)

Введем новые функции, удовлетворяющие тем же (что И фп) .краевым условиям, т. е.

(31.27)

Так как

('^^Е=ад„|- СЙуй, (31.28)

То, интегрируя уравнение (31.26), получаем (прн пфк.)

К, - а2„) | г„%е~‘ ‘Л = 0, (31.29)

ЛЧ = Г (Т2„?2„ - ?,«?!„) de = 0; (31.30)

Б’

1

4»=| (?,«?2,+м>2„) л =0. (31.31)

Интегрируя выражения (31.30), (31.31) при n—k, получаем

Sin йхп I 1 sin (2яя - — ап) . 1^ sin (2л/г - f~ gin) ggj

2а1п Т 4 — ‘ 4 (2лп а1п) ’ ' * J

[I — cos (2л:п — аы)] I 1 — cos (2 лn + aui)

J ____________ Ша ___ »_ I» I

2а1„ 4 (2л«—а1д) 4(2л«+л1л)

(31.33)

Основная особенность рассмотренной задачи заключается в юм, что собственные значения |3?г получились действительными числами (а не комплексными), несмотря на то что уравнение

(31.1) содержит слагаемое с нечетной производной по времени, т. е. прямолинейный шланг с движущейся жидкостью является консервативной системой.

«1=2 (31-34)

Сп=с,,Л-1с-2п. (31.35)

Общее решение является комплексной функцией, т. е.

112'=— 2^21 ~j - 1Ч 22- (31.36;

После преобразований получим

U21— V с1п (ср1п COS?„t + Т2к sin рят) +

-]- V с2п (Ъп °os %t — cpln sin ); (31.37)

«22= V clrt (<p2n C°S ?nt + <Pie sin

Я О

+ 2 f2n(?i» cos3„t - <f2,, sin 3„t). (31.38)

Рассмотрим свободные колебания, вызванные начальным от­клонением шланга о г положения равновесия. В наиболее общем случае в начальный момент времени возможны отклонения */21 (е, 0) — li2Q и скорости й21 (б, 0) = W20 точек осевой линии шланга.

Потребуем, чтобы при т=0 выполнялись условия [действи­тельная часть и21 общего решения (31.27) и его первой произ­водной по времени были равны функциям и2о и йго], т. е.

«я (е, О)=И20(е, 0) = v (С1(|ф1„-)-С2«Ч>Зп); (31.39)

ЙЯ(*. 0) = “2о(в,°)=^2 (C, A’f2n — C2n9rfflJ. (31.40)

П=0

Для получения решения необходимо определить произволь­ные постоянные Сщ н с2п. Для этого умножим уравнение (31.39) на раф2к, а уравнение (31.40) на ф(К н сложим полученные выра­жения, т. е.

«2оРп? а< + «ийк= ciA (91»?ъ+Ы1к) +

+ 2 2"?2к ~ ч>1“¥ 1к)- (31.41)

191

Интегрируя (31.41) от 0 до 1 с учетом соотношений (31.30) — ■(31.31), получаем

( = (31.42)

Второе уравнение ДЛЯ определения неизвестных Сщ и С2п найдем, умножив выражение (31 39) на (ЗпФш, а выражение

(31.40) на ф2к. Вычитая и интегрируя, получим

С (“20,3оЧ>1к-"2,?к)^= —(31.43,)

О

Для определения неизвестных Сп И С2п получаем систему уравнений

(31.44)

Ф2„= - КайгЯЙ,

Где (ч-1)Хъ„ + Ижу,„) с! е; (31.45)

| («2оРи?1и — И2(??2к) Л - (31.46)

Из системы уравнений (31.44) имеем |Ф1И м!,1,,’ I

_ к» г«/™'! ,

Й [№)2 *-(Ог]: С2п_й[№)а+№’)а|' (3!’47)

Рассмотрим случай, когда на ил ант действует сосредоточенная осевая си­ла Р| (безразмерная), направленная при колебаниях по касательной к осевой линии шланга (рис. 31-3) в точке ее приложения (следящая сила). Для шлан­га, не обладающего изгибной жесткостью, это возможно, если считать, что в точке приложения силы Р. разрыва первой производной прогиба и по коорди-

Считая, что до приложения силы Р шланг был натянут силой <2ю, имеем Он = <3ш + - у-; Оа = <?ю—-у - > о, (31.49)

Є С, и= ОЦ1 —

Для каждого из участков имеем уравнения малых колебаний д^щ д2и> д2и

+ 2лі”» ЛаГ-<3,-Я0>

А2«2 а2и2 _ <32и2

Лг+а,,"‘;*1 — ”*2^=а (3|-5,)

Решение каждого из уравнений ищем в виде

«і = ище1*; «2 = ааови - (3! .52)

После преобразований из (31.50), (31.51) получаем два уравнения:

О=0; (31.53)

2піШД Он 10 С? п

2и1и'0Х, Х2

И20 + 7^ “20 ~ ~р. “20 = 0. <31.54)

412 У12

ІІолагая

Кю — А^е1^ ^е; ио~ АъР*^ (31.55)

Олучаем два характеристических уравнения:

Л(1)+«11Х/гї1> —й21Х2=0; (31.56)

£(2) + «12и(2) — Я22Х2 = 0, (31.57)

Пе

2піте>0 I

Ап -=

0„ ’ Он

2п]і0ц 1

Й,2="о^:°22="Й7-

Корни уравнений (31.56), (31.57) соответственно равны:

*14 -1/а‘1+4аг1 )

Матрицу перехода получим (воспользовавшись методом начальных пара­метров) от сечения е=0 к сечению е=0,5. Для первого участка имеем

Л*1)« 41>в

«ю = с1е 1 --с2е ; (31.63)

И[0=Ск^е 1 е

Полагая

“№ (0> = “'о1: “'ю (°) = “м*’: (31-&4)

Находим С и с®:

;о(1));

(31,65)

«у>-*}4 (~“Ц>*»1,+«и1>)-

Подставим С1 и Са в выражение (31 63), получим (переходя к векторной форме записи) уравнение

Йю = А<1>&Щ>, (31.66)

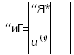Где

#}« 41}е Л(1)Е

»РМ А1*« ьР* ‘

2 ) /4»е 2 - *<*>«

4‘>_ /;<■)

(31.67)

Полагая в е=1, получаем матрицу перехода для первого участка.

Для получения матрицы перехода на втором участке за начало отсчета целесо­образно взять начало второго участка. Матрица перехода Л(2) от сечения е—0 к сечению р,= 1 на втором участке получается из матрицы Л!1) заменой б}1*

На /г{2* и на в результате чего

5» = ^(2)М^’: («й> = «ю|,=1). (31.68)

Окончательно имеем

В» (1) = А™ (1) Л(1) (I) Ц'о> = (31.69)

При е=] ДОЛЖНО ВЫПОЛНЯТЬСЯ условие «20 (1) =0, или

И2о(1) = а!1Чо1) = 0, (31.70)

Где й|2(3* — элемент матрицы А&>.

Значения К, при которых выполняется условие (31.70) являются собствен­ными числами задачи. Так как в общем случае собственные числа X могут быть

194

Комплексными (Я=а+і'Р), то и элементы матрицы Л будут комплексными числами, т. е.

4?> = °рУ + ‘а$- (31.71)

Поэтому из (31.70) получаем два уравнения (так как «іо(,)=Ці(1)+ім2(П): И‘Ч(,)-а<ЇЦ,)= 0;

1 (31.72)

И^;‘,)+ойЧ1)=о.

Из системы (31 72) следуют два условия:

Лй> = 0;о^>=0. (31.73)

Совместное решение (численное) системы (31.73) позволяет определить

А„и Р11 н тем самым найти собственные комплексные числа:

Ху = а'# ± (31.74)

После преобразований элемент «|2(3) матрицы А(3> равен

Л(3) _

(31.75)

Рассмотрим два возможных случая обращения 0|2'3) в нуль (полагая в ^1) = й + |р):

41} й(1) 42) й(2)

Е2 — е 1 = 0; е —с1 =0. (31.76)

Из первого уравнения (31.76) следует

/■’■•е™' < 1, (31.77)

> возможно только при а=0.

При а=0 из (31.77) получаем

2*РУ2 = 2яш (31.78)

Лп<1и (3179)

1,2 У <315* - Ро + - у - - («1 - «1>

Из второго уравнения (31.76)

„Л4

I выражениях для корней М ] X = а + ,

«ю(а, Р) = Уз~VI + «20(«» Р) =

«10 + *«20 = ®»

У2 бЬ 2ау2 сЬ 2ауг — сое 2Руг

У2 в1п 2РУ2___ ,

СЬ2ау2 — сое 2Ру2

/21^0 П1^0

Он : 1,3 ~ 012 ;

(31.85)

>=~^У РЦ)~рч+ - у--('П-п20 «I (31.86)

, = - тр ^ - - у — («1 - «!) < (31.87)

Зависимости от параметров потока ь»о, Ро и от безразмерной сосредоточенной силы Р{

Уравнения (31.83) — (31 84) позволяют определить критические параметры потока (при определенной сосредоточенной силс Р1) и соответствующие нм частоты колебаний шланга. Критические параметры потока соответствуют слу­чаю, когда а—0. Из уравнения (31 83) получаем

(7з-У1)(1 — сое 2Ру2) (I — сой 2ру4) = 0, (31.88)

Или (так как при РхФ 0 Уз—VI¥=0)

Р(1) = ^. (/2 1,2,3...), (31.89)

72 74

Чисто мнимыми и разными для каждого из участков шланга, т. е. общих час­тот, характеризующих движение всего шланга, нет. Кроме того, из решения следует, что при наличии следящей силы задача остается консервативной.