Механика трубопроводов и шлангов

Малые колебания стержней, взаимодействующих с потоком воздуха или жидкости

Прежде чем переходить к выводу уравнений малых колеба­ний и их решению, сформулируем основные задачи, возникаю­щие при эксплуатации реальных конструкций, сводящихся к расчетной схеме гибкого стержня, где возникает необходимость исследования динамики этих конструкций.

Анализ возможных вынужденных колебаний гибких стерж­ней требует - знания спектра частот, чтобы изменением конструк­тивных параметров отстроиться от резонансных режимов. Кро­ме того, имеющиеся методы определения частот для систем с распределенными параметрами [60] позволяют определить н формы колебаний, которые необходимы для приближенного ре­шения более сложных задач динамики стержней (решение урав­нений малых колебаний с использованием принципа возможных перемещений или других методов приближенного решения). Поэтому первой задачей при исследовании динамики гибкого стержня, взаимодействующего с потоком, является за чача опре­деления частот и форм стержня с учетом параметров потока (скорости потока t>o и его направления — угла «). Следует от­
метить, что определение частот и форм колебаний гибкого стерж­ня, находящегося в потоке, требует введения ограничения на аэродинамические силы (их надо считать не зависящими от движения стержня, т. е. равными статическим значениям). В этом случае частоты будут зависеть только от напряженного СОСТОЯНИЯ 13 стержне, что и должно быть.

Как известно, при определенных режимах обтекания стерж­ня возникает обтекание со срывом вихрей (образуются вихри Кармана), что приводит к появлению аэродинамических сил (сил Кармана), перпендикулярных к нормальной составляющей скорости потока (нормальной к осевой линии стержня). Поэтому второй задачей является определение установившихся режимов колебаний сгержня, вызванных силами Кармана.

Третья задача, возникающая при исследовании динамики стержня в потоке, связана с анализом устойчивости малых ко­лебаний сгержня в потоке.

Как было показано в § 20, аэродинамические силы (состав­ляющие Ддпх., к. н Л<7/_ Г/) зависят от динамических состав­ляющих их. вектора состояния стержня (от их первых производ­ных по е и т), причем эти силы являются иеконсерватнвнымн, что при определенных сочетаниях между параметрами конст­рукции и параметрами потока (критические параметры) може* привести к неустойчивым режимам колебании Определение этих критических параметров является наиболее важной для практики задачи и в то же время наиболее сложной при ре­шении.

В начале данной главы указывалось, что динамические ха­рактеристики стержней (спектры частот, критические параметры системы стержень — поток) существенно зависят от начального напряженного состояния, которое вызвано действием аэродина­мических сил (или гидродинамических сил) при равновесии стержня в потоке. Поток воздуха или жидкости отклоняет стержень от его естественного состояния (например, от верти­кальной плоскости, в которой расположен провод под действием сил тяжести), одновременно меняя его напряженное состояние. Новое равновесное состояние стержня в потоке может очень сильно отличаться от начального и столь же сильно могут от­личаться и спектры частот.

Определение частот стержня при отклоненном состоянии осложняется еще и тем, что стержень принимает пространствен­ную форму, что приводит к зависимым по всем трем координа­там уравнениям малых колебаний. При определении частот стержня, например, круглого сечения, осевая линия которого есть плоская кривая, уравнения расщепляются на систему двух уравнений колебаний в плоскости осевой линии и одно уравне­ние относительно плоскости осевой линии, что упрощает пх ре­шение.

Векторные уравнения малых колебании стержня. Рассмот­рим малые колебания стержня в потоке относительно состояния равновесия. Считая, что динамические составляющие всех векто­ров, характеризующих состояние стержня, являются малыми, можно считать, что

И= Д7г; Др; ДЖ;

У—хо Д*; Я=Яи~'' 1А=!Ло-|-Др-» (24.1)

& Л& (Дй^й, Л{>2=4, =

Ф и у — малые углы),

Где векторы с индексом нуль характеризуют состояние равнове­сия с1ержня; Аи, Д() и другие — дииамические составляющие соответствующих векторов.

Остановимся более подробно на соотношениях (24.1), в ча­стности, рассмотрим векторы М, (?, к. Например в связанных осях [в базисе {е*}] векторы в дальнейшем будут записываться в виде

Ж=Х’(,и0,. + Д/И,)ё,.,

<3=£(0ш + ^е„ (24.2)

У — V -[- Ду() е,

Такое представление компонент векторов (с выделением ста­тических сосгавляюших с индексом нуль) удобно при преобра­зованиях, по следует помнить, что векторы

Ло=^.И, оё,; $0° ='^’0,,/,; «о^УдЯ,

(24.3)

Не равны соответствующим векторам в статике.

Представление векторов в виде (24.3) позволяет в уравнени­ях движения (малых колебании) сократить уравнения равнове­сия. Векторы М, () можно представить и в базисе {Г,}:

Дополнительно к перечисленным векторам в уравнения движе­ния (21 10)- (21.11) вхидят еще два вектора: п(п=и) и &>, кото­рые также являются малыми.

Воспользовавшись общими уравнениями (21.10) — (21 12), получим уравнения малых колебаний, подставив выражения (24.1) и сокращая уравнения равновесия,

(24.5)

= ХЛЛ) (-ЛххЖо+^хДУ + Л^--(-Д?*; (24.6)

ДЛ7 = Л(г)Дх; (24.7)

-|р + ^х^-=«хё,. (24.8)

При малых колебаниях из уравнений (21 14), (21.15) полу­чаем еще два уравнения вида

*, X Дй: (24.9)

-=іг - <*-'<»

В результате имеем шесть уравнений с шестью неизвестны­ми; і, Л(>, АМ, Ах, со, ДО. Можно от вектора її перейти к вектору м, но при этом вместо уравнения (21.13) перейти к уравнению (с учетом малости Аі%)

—Ь ха X и=е1 — £10 =• Д&3£?2 — Ля^з - (24.11)

Уравнение (24.10) можно представить в записи, бплее удоб­ной для преобразований.[запись, справедливая в базисе {с,}1,

-^-+Л7( + Л„ДЙ=0 (й = }и, ё,). (24.12)

В ряде задач, где определять ДО н 17 не требуется, исполь­зуются уравнения (24.8) н (21.21). Уравнение (21.21) при малых колебаниях принимают вид

-I—£+^=°- ('24-|3>

(При переходе к вектору ДО уравнение (24.13) обращается в тождество, так же как и при нелинейных колебаниях для обще­го случая зависимость шик от углов <0у).

Рассмотрим более подробно уравнение (24.12). В представ­ленной форме заилен оно связано с базисом {?*■}. При решении уравнений в проекциях па неподвижные оси удобнее перейти к базису {Ї,}, т. е. воспользоваться соотношениями

<?2—^2111 *22^2 “Ь ^2^3!

11^1 —|— А*42^2“}

Что приводит к записи уравнения <24.12) в форме

=(а*>^2, - до^.и) ~н+(д®зй - а»2^52) к +

Где и— V агГІ4.

І

Так как з неподвижных координатных осях

И = V (Ху - х]0) і} - = V Xjij,

(24.18)

Можно отметить несколько замечаний относительно получен­ных уравнении. Уравнения (24.6), (24.7) получены в связанной системе координат. В этой системе справедливо физическое уравнение

Д. М^Л^Дх,. (24.19)

Соотношения (24 19) устанавливают связь (об этом говори­лось в гл. II) межту приращениями кривизны проекции осевой линии и а главные плоскости сечения стержня и локальными приращениями компонент вектора Л/.

Получим выражения, устанавливающие связь между прира­щениями компонент векторов Л/ И <2 в неподвижных(АМХ{, АС}%.) и связанных осях (ДЛ4г, ДС?|).

(24.20)

(24.21)

(24.22)

(24.23)

(24.20) в базисе {Ij}

ДЛЦ=2 + АЛ1/5,). (24.25)

= 2 №'-"й*Л + (24.261

Где

Cos ф0 sin

Д&12= — Й2А&2 — М3Д&1 - f - cos cp0 cos % cos &0Д&3;

Д£13= Ј?2A&i — А, з.^й&2 -J - cos % cos cp0 sin &0Дч}3; (24.27)

Д^21 = — cos <p0Aft3, Ak22~ — f&iLbl — cos ©o sin <p0A&3;

Д^2з= ~ sin <p0 sin &(1й&з4-й^1;

AA>3i=&nA&2— sin Фо sin %ЛН3;

Д£32 =^i2^&2“ ЙД&1 + sin ’-|>0 cos ср0 cos &0Л93;

Д£83=Л’?зД&2-[-&з2Д9-1-(- sin ф0 coscp0 sin &0Д&3.

^Соотношения (24.25), (24.26) можно представить в вектор­ной форме записи:

Д7Йл=(/С<о))-гдЖе + /СЛ1А«; (24.28)

BQx=(KW)' bQe+KQД». 24.29)

Где (/С(0>)т транспонированная матрица. Элементы матриц Км и Кц даны в приложении № С.

Из соотношений (24.28), (24 29) следует, что приращения компонентов векторов в базисе {г,} зависят не только от при­ращений компонент вектора М, ко и от статических составляю­щих Л'1,0 и Qio, которые при деформации стержня изменяют свое ориентирование по отношению к базису {^} и поэтому дают до­полнительные приращения, зависящие от углов поворота се­чения.

Получаем окончательную систему уравнений малых колеба­ний гибких стержней в потоке:

(24 30)

Дт? ое

+ - х йд*,+ д-г х м0+ё1 X Л&+ Д(Г<,+

(24.31)

ЛХ_=ЛД^; (24.32)

= к°д§А. _ К°Кя^е-, (24.33)

—/С(2)Д®,=0: (24.34)

Дв

- =_йд5^ 5 (24.35)

* йе “ *

- (24.36)

С? Т

Где векторы с индексом г представлены через проекции в бази­се {Г,}, а с индексом е — в базисе {ё*}.

Система из семи уравнений (24.30) — (24.36)_содержит семь неизвестных векторов: Дма., А@х, А()е, АМС, ыс, Акс, А#с-

Уравнения движения в скалярной форме. Уравнения (24.30) — (24.36) представляют собой смешанный вариант, когда часть уравнений [уравнения (24.30) и (24.34)] представлены через векторы в неподвижной системе координат (с индексом х), а часть в подвижной (связанной) системе координат (с индек­сом е).

В тензорной форме записи получаем следующие уравнения: дьх

«, - V------------- Г11+д?“к; (24-37)

TOC o "1-5" h z ох, де 1С

Г <4 л

Ук/ —------- ----- у - (Д-Мк) - 0,0Ш; - ек, уАх,0Л^0 +£К|1дд, =

=^^к+81кДр. в1{; (24 38)

LЛ■lк~AJjAXj (при к ф у; Л|{у=0);

Ддк=$ —£$ДОу;

С)«л

—- ^2/^ЗкД^У “Н ^3/^2к Д^/==

^ = -^+вк! ЛоД»/;

<ШК

К

К}3'— элементы матрицы К(3К равной КЮ=КоКя%

Ой форме записи имеем

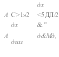%ДЖ 5 -{- Х30ДЖ2 /И30Дх2 -{- Ж20Дх3:

= Д^1”|- Д^с,;

— х30 дм х 4- х1идж3—ж10 Дх3 -{- уи'30дх1 -}- др3

Д*!^—^4цДх11 ДЛ'/з—у422^^2» ДЛ'/з—у^ззДх Д0К=,(Й, Д(2^ + Й])Д»|) (к=1, 2, 3),

Д*1 = —Ь 7-2(А^ + х30 д&25

Дь

Д«2= —------- х10Дй3 - [- к^ДО,;

Д*з= {>^~ ’ [ хю Ай2—«го

£?Д0( д±&2 (Ш3

Дх

Уравнения малых колебаний в связанной системе координат.

В системе уравнений (24.30) — (24.36) только уравнения (24.30) и (24.31) записаны через векторы в неподвижных координатах Для получений уравнения поступательного движения элемента стержня в связанных осях воспользуемся уравнением (24.5), из которого после преобразований имеем

Д?, |-Д~Ча,- (24.50)

В чанном случае уравнение (24.33) является лишним (оно может быть полезным, если надо будет после определения Л (Л найти Д(?д).

Уравнение (24.34) при переходе к локальным производным принимает вид

-~ + АЯ + Л0Л8е=0. (24.51)

В результате имеем систему уравнений в векторной форме

Записи (опуская значок тильды в обозначениях локальных про­

Изводных) :

- — Л«ДУв-АсД*г=Д? е+Д?«; (24.52)

/0_й»_йдл^ - Д. Д/Й,+Л лг-Я — Л„дУе = Д! те 1-Д|%; (24.53)

Дг де.

Д7Йе = ЛЛхв;

+ А~ие + Лс Д&„=0;

+ Л„ Д9„ - Дх, 0;

TOC o "1-5" h z де 1 ‘ '

С>АД,

<?Т5

II 0 Озо —Ого

—^60 0 (210

II Сго С? ю ®

Система из шести уравнений (24.52) — (24.57) содержит

Шесть неизвестных векторов: йр, Д&, ДМе, Дхе, со, Д1%. В скаляр­ной форме уравнения, соответствующие системе (24.52) — (24.57), сличаются от уравнений (24.44) — (24.49) только из-за выраже­

Ний (24.52) и (24.55), которые в тензорной и скалярной форме записываются в виде

«1 ~~д,„4-Л (24.58)

-"+=«,Ло«,- - ЧцД», =0, (24.59)

Или в более подробной форме записи:

<52«! д^х

.х3 Оз0"^У’2 “I - ж ~— ^Я»

ПЛ~-^-+«зоД*1-0,оД«з+*,оДУл-«г. Д9,= =Д;2; (24.60)

~ ~ ^ Х1»Д«2=Д«з;

Дих.

Г У20И3 — ХЗУ^2 0;

—1“хзои1 —х10нз=Д^; (24.61)

-^- + *10«2 - *20« 1 = ' * Д&2-