Машины, работающие по циклу Стирлинга
ИДЕАЛЬНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ЦИКЛЫ
Первый и второй законы термодинамики, по-видимому, применимы ко всем тепловым машинам, в том числе и к двигателям Стирлинга.
Первый закон термодинамики. Первый закон термодинамики, известный как закон сохранения энергии, отрицает возможность создания постоянно действующего двигателя (или некоего термодинамического «черного ящика»), который производил бы работу без затраты энергии. Первый закон термодинамики требует равенства количества подведенной к машине и отведенной от нее энергии (в любой форме). Рассмотрим энергию топлива (бензин и воздух), подводимого к двигателю внутреннего сгорания с искровым зажиганием. Бензин и воздух соединяются в процессе горения, образовавшиеся горячие газы приводят в движение двигатель. Из всей энергии, содержащейся в топливе, около одной трети преобразуется в полезную работу двигателя, другая треть отводится системой охлаждения, а оставшаяся треть энергии как низкопотенциальная тепловая энергия выбрасывается с выхлопными газами. При прекращении подачи бензина двигатель останавливается. Этот пример — прямое проявление первого закона термодинамики, в основу которого положены различные опытные данные.
Второй закон термодинамики. Второй закон термодинамики, возможно, менее, понятен. Одна из формулировок второго закона гласит, что невозможно создать периодически действующую систему с потреблением теплоты из некоего резервуара и превращением ее полностью в работу. Первый закон термодинамики говорит о том, что полученная работа никогда не может быть больше подводимой теплоты, в то время как второй закон уточняет это положение и утверждает, что работа должна быть всегда меньше. Применительно к бензиновому двигателю внутреннего сгорания второй закон термодинамики отрицает возможность превращения всей подводимой энергии, содержащейся в топливе, в полезную работу. Некоторая часть этой энергии должна непременно теряться в виде теплоты, отводимой системой охлаждения или выхлопными газами.
Этих важных положений достаточно для освещения поставленных в книге целей. Для более полного ознакомления с первым и вторым законами термодинамики и вытекающими из этих законов выводами читатель может обратиться к любому стандартному учебнику по технической термодинамике, например к книге Уолласа и Лининга [7] и др.
Термический к. п. д. цикла. Отношение произведенной работы W к подведенной энергии Q есть термический к. п. д. цикла, т. е. г] = W/Q. В большинстве случаев очень важно максимизировать к. п. д., поскольку он характеризует часть полезной энергии, содержащейся в литре горючего (бензина или нефти). Поэтому, принимая во внимание то обстоятельство, что по второму закону термодинамики термический к. п. д. цикла всегда меньше единицы, важно стремиться к его максимально возможному значению.
Термический к. п. д. ццкла Карм. Для любых заданных условий максимальный термический к. п. д. зависит только от максимальной и минимальной температур цикла и определяется формулой
„ ____ Тмакс Тмин
Чмакс _
• макс
Данное выражение является очень важным и имеет особое название — к. п. д. цикла Карно. Это максимально возможное значение термического к. п. д. достигается при передаче теплоты к системе и от нее соответственно при температурах Тмакс и Тмин.
2-2. р, V- и Т, 5-ДИАГРАММЫ
Процессы, протекающие даже в самой простейшей тепловой машине, настолько сложны, что нет возможности точно рассчитать происходящее. Вместо этого принимается некая теоретическая модель, в которой идеализированы некоторые условия протекания процессов с тем, чтобы в какой-то степени иметь возможность провести анализ работы машины. В этом случае работа большинства типов машин может быть упрощена предположением о последовательно повторяющихся термодинамических процессах, называемых циклом. Обычно каждый процесс рассматривается в отдельности
и предполагается, что изменения термодинамических функций[8]Происходят по мере перехода рабочего тела из одного состояния в другое; при этом одна из функций остается постоянной. Важными термодинамическими функциями являются: давление (р), объем (У), температура (Т), внутренняя энергия (U), энтальпия (J) и энтропия (S).
Цикл, состоящий из последовательных процессов, в каждом из которых одна из термодинамических функций остается постоянной, а другие меняются, может быть изображен графически по-разному. Два таких способа значительно облегчают анализ работы тепловых машин. Это р, V- и Т, S-диаграммы.
|
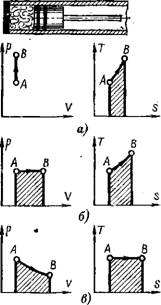
Рис. 2-1. Термодинамические процессы в р, V- и Т, S-днаг - раммах. |
|
А — нагрев при постоянном объеме; б — нагрев при постоянном давлении; в — нагрев прн постоянной температуре. |
Указанные диаграммы являются важными, поскольку площадь на р, V-диаграмме представляет собой произведенную работу, а площадь на Т, S-диаграмме — передаваемую теплоту. В качестве примера рассмотрим рис. 2-1, где показан поршень в закрытом цилиндре. В объеме между поршнем и торцом цилиндра находится некоторое количество газа; можно принять, что такому положению соответствует точка А на р, V - И Т, S-диаграммах. Если теперь газ будет нагреваться через стенку цилиндра от некоего внешнего источника, то возможны различные случаи. При неподвижном поршне объем остается постоянным; нагревание газа приводит к повышению его давления и температуры; в этом случае работа не производится (рис. 2-1, а). Если поршень будет иметь возможность свободно передвигаться, а процесс подвода теплоты регулироваться
Таким образом, чтобы давление или температура оставались постоянными, то рассматриваемый процесс изобразится на рис. 2-1, бив. В обоих этих случаях газ совершает работу за счет увеличения занимаемого объема, поскольку в систему подводится дополнительное количество теплоты.
2-3. ЦИКЛ КАРНО
Цикл Карио — это термодинамический цикл, состоящий из четырех последовательных процессов (рис. 2-2).
Для рассмотрения работы двигателя по идеальному циклу Карно предположим, что имеется поршень и цилиндр (см. рис*. 2-2). Далее предположим, что цилиндр полностью изолирован, а поршень имеет возможность перемещаться в цилиндре без трения; кроме того, будем считать, что утечки рабочего тела из цилиндра отсутствуют.
По нашему желанию головка цилиндра может быть принята либо с очень высокой теплопроводностью, либо быть полностью теплоизолированной.
Предположим, что в начале цикла поршень находится в верхней мертвой точке; объем между поршнем и оболочкой цилиндра максимальный. Давление и температура рабочего тела минимальны; на рис. 2-2, а это соответствует точке 1. Пусть теперь поршень движется к головке цилиндра; при этом происходит сжатие рабочего тела, что на рис. 2-2, а показано процессом 1-2. В этом случае предполагается, "что материал головки цилиндра обладает высокой теплопроводностью, а коэффициент теплопередачи бесконечно большой; вследствие этого процесс протекает изотермически (при постоянной температуре). Работа, затраченная на сжатие газа, и отведенная от него теплота показаны заштрихованными площадями соответственно на р, V- и Т, S-Диаграммах. Поскольку процесс изотермический, количество отведенной теплоты в точности равно затраченной "работе.
|
|
|
|
|
А) |
|
Т |
|
~TMi |
|
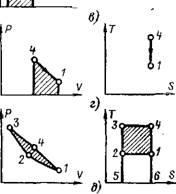
Рис. 2-2. Цикл Карио. |
|
А — изотермическое сжатие; б — изо - энтропическое сжатие; в — изотермическое расширение; г — изоэнтропнче - ское расширение; д — цнкл Карио в Р, V - и Т, S-диаграммах. |
Для второго процесса — изоэнтропического сжатия (рис. 2-2, б) считается, что головка цилиндра полностью теплоизолирована. При движении поршня по направлению к головке цилиндра теплота
не может быть отведена от газа, поэтому в идеальном случае энтропия остается постоянной. Этот процесс протекает с уменьшением объема и увеличением давления и температуры газа. Работа, произведенная над газом, показана заштрихованной площадью на р, У-диаграмме, а передачи теплоты в этом процессе нет. Два оставшихся процесса расширения — изотермическое (3-4) и изоэнтро - пическое {4-1) показаны соответственно на рис. 2-2, виг.
В результате объединения этих четырех процессов получится цикл вр, У - и Т, S-координатах, показанный на рис. 2-2, д. Заштрихованная площадь, ограниченная линией 1-2-3-4 на р, У-диаграмме, представляет собой полезную работу за цикл. Аналогично площадь 4-3-5-6 на Т, S-диаграмме характеризует подведенную в цикле теплоту. Площадь 1-2-3-4 — теплота, превращенная в работу, а площадь 1-2-5-6 — теплота, отводимая от цилиндра за цикл. Из этой диаграммы ясно, почему цикл Карно имеет наибольший из возможных термический к. п. д. При заданных температурных условиях, т. е. при заданных значениях Тмакс и невозможны циклы с ббльшим отношением "^площадей 1-2-3-4 и 4-3-5-6,
. ^ w Пл. 1-2-3-4
Следовательно, термический к. п. д. т] =------------------- =------------------- дол-
Q Пл. 4-3-5-6
Жен быть наибольшим.
В термодинамическом анализе должны использоваться абсолютные температуры. В Т, S-диаграмме за нулевую температуру принята температура, равная —273° С (О К); вследствие этого, если требуется отвести теплоту, эквивалентную площади 1-2-5-6, то она может быть значительной.
Очевидно, что к. п. д. цикла Карно (и это вообще относится ко всем двигателям) может быть повышен либо путем увеличения температуры Тмакс, либо уменьшением температуры Тмин. Предельное значение максимальной температуры Тмакс ограничено конструкционными материалами двигателя и называется термическим пределом. За наименьшее возможное значение минимальной температуры Тмин принимается температура охлаждающей воды или воздуха, обычно находящихся при окружающих атмосферных условиях.
Сконструировать двигатели, работающие по циклу Карно, практически невозможно: нет конструкционных материалов с совершенными теплоизоляционными и теплопередающими свойствами; движение поршней в цилиндрах происходит с трением и имеются потери, связанные с утечками газа. Однако наибольшие трудности возникают из-за малой разницы в углах наклона кривых на р, У - диаграмме, описывающих изотермические и изоэнтропические процессы в *газе (например, в воздухе); вследствие этого ничтожно мала площадь на р, У-диаграмме (рис. 2-2, д), если только не используются давление в несколько миллионов атмосфер и ход поршня — несколько метров. При таких предельных параметрах двигатель становится громоздким, тяжелым и совершенно неспособным производить работу на преодоление собственного трения. Несмотря
ГСС. ПУБЛИЧНАЯ НАУЧНО-ТЕХНИЧЕСКАЯ БИБЛИОТЕКА СССР
На невозможность практического использования, цикл Карно полезен для предварительного изучения работы любого двигателя. К тому же при некоторых изменениях, приводящих его к циклу Ренкина, цикл Карно является характерным для работы паро - жидкостных машин, таких как, например, поршневые паровые двигатели, паровые турбины и фреоновые холодильные установки.