Машины, работающие по циклу Стерлинга
ОПТИМИЗАЦИЯ ПАРАМЕТРОВ КОМПОНОВКИ
Из приведенных выше уравнений для цикла Шмидта очевидно, что полезная мощность за цикл и тепловые нагрузки на теплообменники, определяемые в зависимости от общего вытесняемого объема VT9 есть линейные функции частоты вращения вала двигателя N, Давления рабочего тела рмакс и габаритов двигателя. Влияние же четырех основных параметров т, Ky а и X на характеристики двигателя менее очевидно. В особенности неясно, какую из комбинаций рассматриваемых четырех параметров необходимо выбрать для получения оптимальных характеристик двигателя. Это является
Очень важным обстоятельством, поскольку указанные параметры должны определяться на стадии конструкторской проработки, и, за исключением параметра т, изменить их можно только за счет изменения самой конструкции машины.
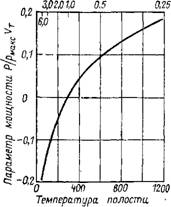
^ Влияние на параметр мощности PI{puaKCVT) каждого из четырех параметров т, K> а и X при условии постоянства трех остальных рассматривается на рис. 5-1—5-4. На рис. 5-1 исследуется влияние отношения температур на параметр мощности для различных температур полости расширения ТЕ> диапазон которых простирается
Как выше, так и ниже температуры полости сжатия Тс = 300 К (а = 90°, K = 0,8, X = 1,0). Вследствие этого приведенная зависимость справедлива и для двигателя и для холодильной машины. При температуре ТЕ > Тс Параметр мощности положителен и плавно возрастает с увеличением температуры в полости расширения. При ТЕ<.ТС машина работает как холодильная установка, и с уменьшением температуры в полости расширения мощность, требуемая для ее привода, постепенно увеличивается. Очевидно, что мощность двигателей можно увеличить за счет применения для цилиндра полости расширения и теплообменников высокотемпературных материалов, а в холодильной машине необходимо стремиться к достижению минимально возможной температуры охлаждения.
Зависимость параметра мощности от отношения вытесняемых объемов при а = 90°, X = 1,0 приведена на рис. 5-2. Из кривых ясно, что при заданных значений т, а и X существует вполне-определенное оптимальное значение Ky для которого параметр мощности максимален. Однако сравнение двух кривых с т, равными 0,25 и 0,5, показывает, что оптимальное значение K не постоянно, а изменяется от 0,75 (при т = 0,25) до 1 (при т = 0,5). При изменении а и X меняется также и оптимальное значение k. Таким образом, единого и «лучшего» значения для K не существует.
Влияние относительного мертвого объема X = VDIVE на параметр мощности при постоянных т, Ьа рассматривается на рис. 5-3. Смысл этого графика предельно ясен: с увеличением мертвого объема свыше определенного минимального значения параметр мощности уменьшается. Мертвый объем должен, по-возможности, быть наименьшим.
|
Отношение температур
Расширения ТЕ, К Рис. 5-1. Влияние температуры на мощность цикла. |
Влияние фазового угла а на мощность цикла при постоянных т, K и а показано на рис. 5-4. Параметр мощности особенно чув
ствителен к изменениям фазового угла в диапазоне от 60 до 120°. Для принятых условий оптимальное значение параметра мощности находится в диапазоне а = 90 -т - 115°.
Изменения параметра мощности двигателя в зависимости от двух параметров: фазового угла а и отношения вытесняемых объе-
|
<Г =0,5 |
|
О 1 Z Отношение вытесняемых объемов K=Vc/Ve |
|
£0,2 |
|
10,2 |
|
5 Л ^ Е Со О U: 3* |
|
О» Е |
|
Rft* |
|
0,1 |
|
I" Qi |
|
О) |
|
О 1 г Относительный мертвый объем X-Vs/VЈ |
Рис. 5-2. Влияние отношения вытесняемых объемов K иа мощность цикла.
Рис. 5-3. Влияние относительного мертвого объема X иа мощность цикла.
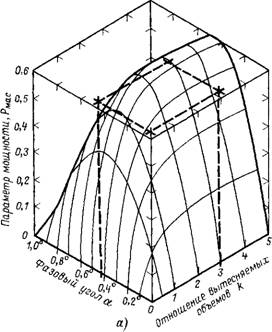
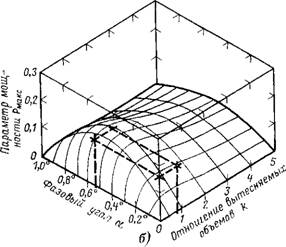
Мов K при постоянных значениях т = 0,3 и X = 1,0 рассмотрено на рис. 5-5. Любое изменение т или X вызывает образование ряда аналогичных, но все же различныхлерекрывающихся поверхностей. Вершина такой поверхности, характеризующая максимальное значение параметра мощности, определяется при заданных значениях т и X оптимальной комбинацией отношения вытесняемых объемов k и фазового угла а. Две поверхности на рис. 5-5 образованы различными параметрами мощности Р/Рмакс^г и P/RTC. Вер - шины этих поверхностей соответствуют различным комбинациям фазовых углов и отношениям вытесняемых объемов. Для поверхности параметра мощности Рм = P/RTC: Аопт = 0,45я рад и kn
Рис. 5-4. Влияние фазового угла а на мощность цикла.
Поверхности параметра мощности Рмакс = Р/РмаксУт- аопт = 0,54я раД
|
60° 90° 120° Фазовый, угол со поворота коленчатого вала |
|
« ОГ А £ I I- Qi I. |
|
Рад и fconr = 2,9. Для |
И &опт = 0,74. Этому странному обстоятельству имеется простое объяснение: оптимизация конструкции по параметру мощности P/RTC соответствует выбору такой компоновки машины, кото-
|
|
|
Рис. 5-5. Влияние отношения вытесняемых объемов K И фазового угла а на мощность цикла. А — параметр мощности P/Rtg (мощность на единицу массы рабочего тела); б—параметр ^/РМаКс^7* (мои*иость' ограниченная габаритами и массой). |
Рая позволяет с максимальной возможностью использовать определенную массу рабочего тела. Оптимизация же конструкции по параметру P/pMaiiCVT приводит к компоновке машины с максимально возможной мощностью, ограниченной максимальным давлением и общим вытесняемым объемом. Максимальное давление рабочего тела является важным конструктивным параметром, влияющим
|
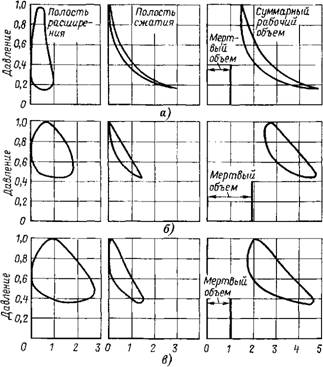
Рис. 5-6. Рабочие диаграммы для двигателей с оптимальными комбинациями конструктивных параметров. Левые диаграммы даны для полости расширения, средние — для полости сжатия, а правые — для общей рабочей Полости *. А — рабочая диаграмма для цикла, оптимизированного по параметру мощности PIRTQ, б — рабочая диаграмма для цикла, оптимизированного по параметру мощности Р/Рмакс в — рабочая диаграмма цикла с такой комбинацией параметров, как и в случае б, Нос мертвым объемом, уменьшенным до показанного на рис. 5-6, а (т. е. с одними и теми же размерами регенератора и теплообменников). |
На прочность, а следовательно, и на массу машины, в то время как общий вытесняемый объем определяет ее габариты. Отсюда ясно, что оптимизация должна проводиться по параметру мощности
P/pMaKCVT. Однако с момента определения основной компоновки машины по a, Ky т и X может быть использован и параметр мощности P/RTC. Оба эти параметра, P/RTC и Р/рмакCVT) равнозначны и приводят к одной и той же мощности двигателя за цикл.
В качестве примера на рис. 5-6 приводится сравнение рабочих диаграмм для оптимальных комбинаций фазовых углов а и отношений вытесняемых объемов K при постоянных значениях т и X. Для всех трех случаев "давление выражено в долях его максимального значения в цикле, и вследствие этого возможно сравнение рассматриваемых диаграмм. Аналогичным образом для всех трех случаев максимальное значение общего внутреннего объема принимается одинаковым и равным произвольно выбранному значению 4,6. Для каждого случая крайние левые диаграммы относятся к рабочим диаграммам полости расширения, средние — к полости сжатия, ' а крайние правые — к общему внутреннему объему. Диаграмма на рис. 5-6, а получена при следующей - комбинации параметров: аопт = 0,45л; рад, K = 2,9, т = 0,3 и X = 1; оптимальная компоновка осуществляется по P/RTC. Комбинация параметров на рис. 5-6, б следующая: а = 0,54 зт рад, K = 0,74, т = 0,3 и X = 1; оптимальная компоновка осуществляется по параметру Р/рмакCVT. Комбинация параметров на рис. 5-6, в такая же, как и в случае б, но с мертвым объемом VD таким, как в случае а.
Из вышесказанного видно, что две машины, характеризуемые диаграммами на рис. 5-6, а и б, сравнимы по массе и габаритам. Для обоих машин максимальное давление и максимальный общий внутренний объем одинаковые, а мертвый объем в одной из машин в 2 раза больше, чем в другой. Несмотря на это, полезная работа машины в случае б в 1,38 раз превосходит работу машины в случае а. При уменьшении мертвого объема (в) полезная работа машины увеличивается в 2,24 раза. Данный пример убедительно подтверждает правомерность использования для оптимизации параметра Р/рмакс^Т-
Аналогичные сравнения для криогенных газовых машин были проведены Уокером в 1962 г. Использование параметра холодо - производительности QE/pMaKCVT для изучения оптимизации является предпочтительным, поскольку этот параметр при заданных габаритах и массе определяет компоновку машины с максимальной холодопроизводительностью.