Машины для производства строительных материалов

Основы теории дробления материалов

Горные породы, подвергаемые измельчению, представляют собой сложные полиминеральные среды, в которых зерна отдельных ми­нералов связаны между собой силами сцепления. Различают два вида сил сцепления – силы, действующие внутри зерен (внутри-кристаллические), и силы, действующие между зернами (меж­кристаллические). Наибольшее влияние на эффективность измель­чения оказывает вторая группа сил, так как разрушение отдель­ных кусков происходит по наиболее слабым местам – плоскостям спайности. Значение этих сил определяется разнообразными фак­торами и не поддается точному определению. Кроме того, энерго­емкость процесса измельчения в дробильных машинах зависит от размеров, формы и однородности кусков, их физико-механиче­ских свойств, влажности и т. д. Поэтому конечной целью теорети­ческих исследований процессов измельчения является получение (в общем виде) зависимостей между расходуемой энергией и от­дельными характеристиками измельчаемого материала.

Наиболее известными гипотезами, устанавливающими такие зависимости, являются Теории дробления Риттингера и Кирпичева-Кика.

Первая теория. Теория Риттингера (1867) устанавливает взаимосвязь меж­ду работой, затраченной на измельчение материала, и вновь образованной при этом поверхностью кусков, т. е.

MACROBUTTON MTEditEquationSection2 Equation Section 2 SEQ MTEqn r h * MERGEFORMAT SEQ MTSec r 2 h * MERGEFORMAT

Где А – работа, затраченная на измельчение, Нм;

K – коэффи­циент пропорциональности, Н/м;

ΔS – величина вновь образован­ной поверхности, М2.

Экспериментального подтверждения данной гипотезы Риттингер не привел, но предложил методику определения величины вновь образованной поверхности.

Вторая гипотеза. Теория Кирпичева-Кика.

Работа деформации:

MACROBUTTON MTEditEquationSection2 Equation Section (Next) SEQ MTEqn r h * MERGEFORMAT SEQ MTSec h * MERGEFORMAT MACROBUTTON MTEditEquationSection2 Equation Section 2 SEQ MTEqn r h * MERGEFORMAT SEQ MTSec r 2 h * MERGEFORMAT MACROBUTTON MTEditEquationSection2 Equation Chapter (Next) Section 2 SEQ MTEqn r h * MERGEFORMAT SEQ MTSec r 2 h * MERGEFORMAT SEQ MTChap h * MERGEFORMAT MACROBUTTON MTEditEquationSection2 Equation Chapter 2 Section 2 SEQ MTEqn r h * MERGEFORMAT SEQ MTSec r 2 h * MERGEFORMAT SEQ MTChap r 2 h * MERGEFORMAT MACROBUTTON MTPlaceRef * MERGEFORMAT SEQ MTEqn h * MERGEFORMAT (2.1)

Где – деформация тела;

Р – действующая сила.

Согласно закону Гука:

MACROBUTTON MTPlaceRef * MERGEFORMAT SEQ MTEqn h * MERGEFORMAT (2.2)

Где F – площадь поперечного сечения тела;

Е – модуль упругости первого рода.

Напряжение, возникающее при деформации:

MACROBUTTON MTPlaceRef * MERGEFORMAT SEQ MTEqn h * MERGEFORMAT (2.3)

Подставляем (2.2) в выражение (2.1) с учетом (2.3) получим (2.4)

MACROBUTTON MTPlaceRef * MERGEFORMAT SEQ MTEqn h * MERGEFORMAT (2.4)

Оба рассмотренных выражения (гипотезы) учитывают лишь часть затрачиваемой на дробление энергии. В первом случае – на непосредственное образование трещин, а во втором – на упругую деформацию измельчаемого материала.

MACROBUTTON MTPlaceRef * MERGEFORMAT SEQ MTEqn h * MERGEFORMAT (2.5)

Где V – объем измельчаемого тела;

S – площадь поверхности разрушения;

– коэффициенты пропорциональности.

Недостатком данной гипотезы является сложность определения коэффициентов пропорциональности , что снижает практическую ценность уравнения.

Третья теория дробления (Ф. Бонд). Работа измельчения пропорциональна длине трещин, возникающих в процессе дробления (подобно первой гипотезе Риттенгера). В основу теории положено дифференциальное уравнения, связывающее энергию разрушения с крупностью куска.

После преобразований это уравнение принимает вид:

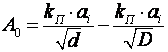MACROBUTTON MTPlaceRef * MERGEFORMAT SEQ MTEqn h * MERGEFORMAT (2.6)

Где – работа, затраченная на измельчение материала;

– коэффициент пропорциональности;

– индекс работы;

D – крупность готового продукта;

D – крупность исходного материала.

Анализируя рассмотренные гипотезы, следует отметить, что ни одна из них не может претендовать на универсальность: одни из них учитывают расход энергии на преодоление упругих де­формаций в материале (вторая гипотеза Кирпичева — Кика), другие увязывают расход энергии с конечными результатами процесса — степенью измельчения (гипотезы Риттенгера и Бонда).

Рассмотренные гипотезы основываются на процессе разруше­ния тел правильной геометрической формы под действием рав­номерно распределенных сжимающих нагрузок.

Однако, как показывают многочисленные исследования про­цесса измельчения полезных ископаемых в дробильно-помольных машинах, разрушение материала происходит под действием со­средоточенных нагрузок, что значительно меняет течение процес­са. В связи с этим непосредственное использование гипотез из­мельчения для технико-экономического и конструктивного расче­та дробильно-помольных машин весьма затруднено и требует введения поправочных коэффициентов, что делает необходимым проведение дополнительных исследований с целью создания обоб­щенной теории измельчения.