МАШИНОСТРОЕНИЕ

ПРОЦЕСС КЛАССИФИКАЦИИ, ЕГО ХАРАКТЕРИСТИКИ И КРИТЕРИИ ЭФФЕКТИВНОСТИ

Под классификацией смеси частиц по

Некоторому признаку в широком смысле слова понимается процесс разделения смеси на две или более частей с существенно различным содержанием этого признака. Признаком клас­сификации может быть крупность частиц, их плотность, форма, диэлектрические и магнит­ные свойства и пр.

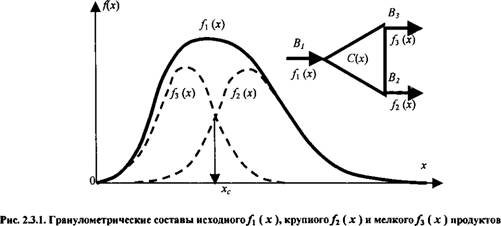
В механических процессах химического производства признаком классификации явля­ется в основном разделение частиц по их круп­ности. При классификации по крупности ис­ходный массопоток сыпучего материала В\ с гранулометрическим составом f\(x), где х - размер частиц, разделяется на массопотоки мелкого Въ и крупного Bi продуктов с грану­лометрическими составами соответственно ufi(x) (рис. 2.3.1). При этом, в виду по­грешности разделения часть мелких частиц может попасть в крупный продукт, а часть крупных - в мелкий. Размер фракции, частицы которой поровну распределяются между круп­ным и мелким продуктом, называется гранич­ным размером классификации хс.

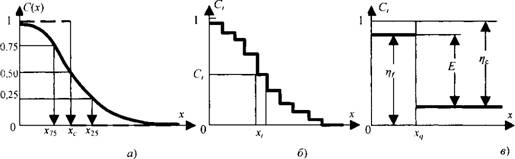
Наиболее информативной характеристи­кой процесса классификации является кривая разделения С(х) (рис. 2.3.2, а), связывающая степень извлечения С(х) узкого класса [.х, х + + dx\ в один из продуктов (обычно в мелкий) с его размером х. По кривой разделения могут быть определены гранулометрические составы продуктов разделения, отнесенные к единице массы исходного материала, и полные выходы ЭТИХ продуктов фз И Ср2-

/з (*) = С(дО/, (*); /2 (X) = (1 - С(*))/, (х);

Оо

Фз = ^C{x)fi (x)dx ; ф2= 1 - фз.

О

Для получения нормированных грануло­метрических составов необходимо разделить /з(х) и/>(*) соответственно на ф3 и ф2.

При идеальной классификации все части­цы мельче хс попадают в мелкий продукт, а все частицы крупнее хс - в крупный. Кривая раз­деления идеального классификатора показана на рис. 2.3.2, а штриховой линией. Наиболее распространенным критерием степени откло­нения реальной кривой разделения от идеаль­ной является острота разделения

К75/25 =xis/x25 >

Где JC75 и Х25 - размеры узких фракций, направ­ляемых в мелкий продукт соответственно на 75 и 25 % (иногда используют другие значения процентов, например, 80 и 20 %).

В практической работе чаще оперируют не непрерывной плотностью распределения частиц по размерам Дх), а массовым содержа­нием фракций конечной (иногда большой) ширины со средними размерами xh где /= 1, 2, ..., т, т - число наблюдаемых фракций, / = 1 соответствует самой крупной фракции, а і - т - самой мелкой. При таком подходе гра­нулометрический состав представлен набором чисел f\,fi, ...,/,„ а кривая разделения стано­вится ступенчатой (рис. 2.3.2, б). В этом случае гранулометрические составы удобно предста­вить векторами-столбцами, а кривую разделе­ния - диагональной матрицей классификации:

Тогда преобразование гранулометриче­ского состава при классификации может быть описано матричными равенствами:

/з=С/ь /2 =(/-C)/i,

Фз = 8иш(/з ), ф2 — 1 ~ Фз?

Где / - единичная матрица; sum - операция суммирования всех элементов вектора.

Матричное представление процесса осо­бенно удобно при применении современных средств компьютерной поддержки инженерных расчетов и расчете каскадов классификаторов.

В промышленных условиях часто кон­тролируют процесс всего по одному контроль­ному размеру xq, обычно разному в разных

6 - 10358 отраслях. В этом случае материал представлен бинарной смесью крупной и мелкой фракций, а кривая разделения приобретает вид, показан­ный на рис. 2.3.2, в. Два значения кривой раз­деления непосредственно связаны с критерия­ми его эффективности: r|y = - степень

Извлечения мелких (по отношению к xq) частиц в мелкий продукт, r\c = 1 - С\ - степень из­влечения крупных частиц в крупный продукт. Разность С2 - С\ = г|у + г|с -1 = £ называ­ется критерием Луйкена - Ханкока. При идеальной классификации г|у = С2 =1,

С, =0, лс =1> Е = ]

В последнее время для повышения эф­фективности разделения и достижения других технологических целей все чаще используют каскады классификаторов - совокупность раз­делительных аппаратов, тем или иным образом связанных между собой массопотоками мате­риала. Для расчета разделения в каскаде при известных кривых разделения (матрицах клас­сификации) отдельных аппаратов необходимо составить матрицу каскада Ск, процедура

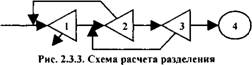
Построения которой показана на примере кас­када, представленного на рис. 2.3.3. При таком последовательном соединении трех классифи­каторов крупный продукт из классификатора 3 направляется на вход классификатора 2, а крупный продукт из классификатора 2 - на

Вход классификатора /. Мелкий продукт всего каскада выходит из классификатора 3, а круп­ный - из классификатора /.

На выходе продукта, гранулометриче­ский состав которого является целью расчета, следует дополнительно разместить коллектор частиц (их может быть несколько) и пронуме­ровать все аппараты каскада, включая коллек­тор. Матрица каскада - квадратная блочная матрица размером, равным числу аппаратов в каскаде. Ее элементами являются матрицы. На главной ее диагонали следует расположить со знаком минус единичные матрицы такого же размера, что и матрицы классификации от­дельных аппаратов. Каждый столбец матрицы принадлежит пронумерованному аппарату. В нем следует расположить матрицу классифи­кации С этого аппарата в строке с номером аппарата, в который из него подается мелкий продукт разделения, и матрицу I - С в строке с номером аппарата, в который из него подает­ся крупный продукт. Все остальные элементы - нулевые матрицы такого же размера, как и остальные. Построенная таким образом матри­ца каскада входит в матричное уравнение

Или

Где F\ - блочный вектор-столбец, состоящий из последовательно расположенных друг под другом векторов fi гранулометрического со­става материала на входе в каждый из аппара­тов каскада; Fq - блочный вектор-столбец, состоящий из последовательно расположенных друг под другом векторов /о гранулометриче­ского состава исходного материала, подавае­мого в каскад (в данном каскаде материал по­дается только в первый аппарат и во всех ос­тальных строках расположены нулевые векто­ры такого же размера, как и /о )» верхний ин­декс «-1» означает обращение матрицы Ск.

Выполняя действия, предусмотренные (2.3.1), можно рассчитать все гранулометриче­ские составы материала в различных точках

/•(4)

Каскада, в том числе вектор /| , описываю­щий гранулометрический состав на выходе из каскада.

Несмотря на разнообразие признаков классификации и принципов действия отдель­ных типов классификаторов, в основе их рабо­ты лежит выявление и использование альтер­нативных сил, по крайней мере одна из кото­рых достаточно сильно зависит от того свойст­ва частиц, по которому осуществляется клас­сификация (например, от размера частицы).

Различают классификаторы непрерывно­го и периодического действия. Наиболее рас­пространены первые; вторые в основном ис­пользуются в лабораторных исследованиях и при дисперсном анализе сыпучих материалов.

По размерности процесса классификации аппараты делятся на поверхностные, объемные и комбинированные. В поверхностных аппара­тах собственно классификация происходит при достижении частицей некоторой контрольной поверхности, например, поверхности сита. В объемных аппаратах разделение частиц реали­зуется в некотором объеме, называемом зоной разделения, за счет организации в ней силовых воздействий на частицы. В комбинированных аппаратах разделение в объеме дополняется разделением на поверхности, ограничивающей зону разделения.

По способу транспортирования сыпучей среды вдоль разделяющей поверхности или в объеме зоны разделения различают механиче­ские, пневматические и гидравлические клас­сификаторы.