ЛАКОКРАСОЧНЫЕ МАТЕРИ АЛ Ы И ПОКРЫТИЯ
Кривые размер — частота его наблюдения
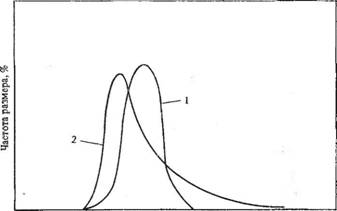
Для большинства определений размеров частиц, полученные кривые размер — частота следуют закону вероятности. Обычное уравнение вероятности применимо к распределению, которое симметрично относительно вертикальной оси, иногда называемому Гауссовским распределением. Поскольку распределения размеров часто «косые» или асимметричные, нормальный закон к ним неприложим (см. рис. 6.5).
К счастью, в большинстве случаев асимметричные кривые можно сделать симметричными, если размер откладывать на лога-
|
Диаметр частицы Рис. 6.5. Кривые распределения: I — симметричное (нормальное распределение); 2 — асимметричное распределение |
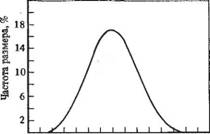
Рис. 6.6. Типичное симметричное распределение (гауссовское или нормальное)
Рифмической шкале (частота остается линейной). Такой вид распределения известен как логарифмическое нормальное [6].
|
5 7 9 И 13 15 Диаметр частиц, мкм |
|
(6-1) |
|
О д/2ЇЇ |
|
„^ L 2о2 J |
|
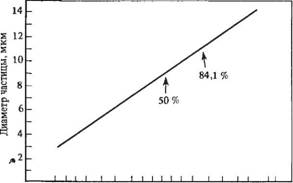
Где F(d) —частота, с которой наблюдается диаметр; п — общее число наблюдений; dav -3t - среднечисловой диаметр; о — стандартное отклонение, о = =^ln(d-dat,)2/ln. Константы dav и о полностью определяют кривую распределения для серии наблюдений. Таким образом, если размеры частиц нанесены на сетку «арифметической вероятности», то совокупная кривая представляет собой прямую линию, где средняя величина (50%-ная величина) — простое среднечисловое dav'- стандартное отклонение о взято как о =(84,1% размера минус 50% раз-
0,2 1 2 5 10 20 40 60 80 90 95 98 99,8—*. Суммарный процент Рис. 6.7. Гауссовская кривая (из рис. 6.6), построенная на основании диаграммы арифметической вероятности |
Уравнение кривой нормального распределения (рис. 6.6) в применении к распределению размер — частота таково:
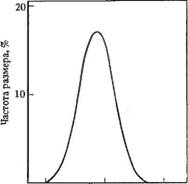
Рис. 6.8. Преобразование асимметричного распределения (из рис. 6.4) в симметрич - иыи график с использованием логарифмической шкалы для размера частиц (мкм)
Мера) = (50% размера минус 15,9% размера) (если график построен с отрицательным наклоном, рис. 6.7).
|
-1 0 1 Логарифм размера, мкм |
Асимметричную кривую разделения, где размер частиц нанесен на линейной шкале (рис. 6.3), можно превратить в симметричную, если диаметры частиц нанести на логарифмическую шкалу (рис. 6.8), т. е. уравнение (6.1) примет вид:
|
(6.2) |
|
Ехр |
|
2 lg2 og |
2>
■F(d)=-
IgOg -/2л
Где dg—среднее геометрическое; og определяется из равенства:
|
V |
|
•В°8 = |
I [Я Ogd-lgrf,)'
In
Параметры lgdg и lg og называются средним логарифмическим геометрическим диаметром и логарифмическим геометрическим стандартным отклонением соответственно. Они очень важны, поскольку полностью определяют логарифмическое нормальное распределение размеров, которое типично для процесса диспергирования [7].
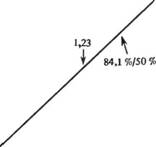
Простой способ построения графика логарифмического нормального распределения размеров заключается в использовании специальной, логарифмически вероятностной, масштабно-координатной сетки (рис. 6.9), где по оси ординат наносится размер частиц, а по оси абсцисс — совокупный весовой (или числовой) процент. Значение dg составляет 50% от величины распределения, a og — 84,1% величины, деленной на 50%-ную величину (или 15,9% величины, деленной на 50%-ную величину, при отрицательном наклоне графика).
Стандартное геометрическое отклонение всегда одинаково в логарифмическом нормальном распределении частиц по раз-
ОД 1 2 5 10 20 40 60 80 90 95 98 99 99,8
Суммарный числовой процент
. .' (_ - г1
Рис. 6.9. График распределения размеров (из рис. 6.4 и 6.8), представленный на —'"1 —' ди-а-ррам^це логарифмической вероятности
І К:'
Мерам, поскольку размеры нанесены на график как совокупный процент, числовой или весовой. Однако средние значения различны и, следовательно, необходимо определить, применяется весовое (dgu,)[7] или числовое (dgC)[8] среднегеометрическое значение диаметра.
|
Средний размер и стандартное геометрическое отклонение |
|
(=1,97) |
|
I I |
|
_1_ |
|
■ 1 ■ ' 1 ■ ' |
Уравнения преобразования Хэтча-Чоэйта [6] дают возможность превратить dgw в dgc. Они позволяют превратить один вид «среднего» в другой и применяются при сравнении измерений распределения размеров, произведенных разными методами:
Исходное значение
Dgm, массовый среднегеометри - ческий диаметр
Требуемое значение Inlgd'
D»c =
V In >
Числовой среднегеометрический диаметр dav — £ nd/J^ л, средне - числовой
Среднеповерхностный
Dv=yind3/ln,
Среднеобъемный
Среднеобъемно - поверхностный
Dw = Y. nd4/Z nd3,
Среднемассовый
Уравнение преобразования 'g = dgm — 6,908-Ig2og
1 g dav = 1 g dgm — 5,757 ■ I gX, !g ds = !g dg,„ —4,605- lg2a, g
Lg dv = gdgm-3,454-lg2ae !g d„s= !g dg„, — 1,151 • !g2o„
Lg dm=g dl!,„ +1,15! - lg2at,
Dgc, медианный
TOC o "1-3" h z среднегеометри - ds
Ческий. диаметр, d„
Числовой dvs
dgm
В преобразовании распределений размеров из числовых в массовые возможны ошибки, так как наибольшие и наиболее тяжелые частицы часто присутствуют в статистически малых количествах. Джексон и др. [8] вычислили ошибки, которые вероятны при таких преобразованиях, и показали, какие шаги следует предпринять для того, чтобы эти ошибки были минимальны.