КОНСТРУКЦИИ С ЗАПОЛНИТЕЛЯМИ ИЗ ПЕНОПЛАСТОВ
Прямоугольные пластины
При действии на пластину равномерно распределенной по поверхности поперечной нагрузки (рис. 3.11) прогибы и напряжения при отсутствии нагрева слоев вычисляют по формулам
|
(3.25) |
|
384 D Qb2z |
|
D' 4hD |
|
■qbm5, |
|
Тзсгс : |
5 qb* - I qb2z Тх
/ Qb*z ту ву = та ~' ~В~) '
D' и Xyzc = ~4hDqbm*-
Здесь W — прогибы в середине пластины;
Ох, оу—максимальные значения нормальных напряжений во внешних слоях (охи Охг, оУи 0^2) и в заполнителе!(аяс. оус), отнесенные в случае заполнителя из армированного пенопласта г условному однородному заполнителю;
Тяге, tyzc — максимальные значения касательных напряжений в заполнителе, отнесенные к условном'1 однородному заполнителю.
Коэффициенты тп определяют в зависимости от условиг крепления кромок пластины согласно табл. 3.4. Обозначение Г См. (3.23). Значения D, В вычисляют по формулам (3.1), (3.2,
При определении 0*1,2, Оухя принимают Е0 — ———, где I=
1 — и2. r 1
Для напряжений в первом внешнем слое, t=2 — для напряжений во втором внешнем слое.
В случае заполнителя из неармированного пенопласта значения £о, В с, Dc вычисляют по формулам (3.4) и (3.20),-а параметр сдвига k — по формулам <(3.7) и (3.3).
Координата точки по толщине пластины г отсчитывается в соответствии с рис. 3.11.
.----" 2А
Фор;мулы (3.23) справедливы при условии -———> i
61 + 0^
(ife^l при определении напряжений и fc^lO при определении прогибов).
А) Поперечный изгиб
В случае отсутствия продольных сил в формулах (3.25) следует положить Тх=Ту=0, коэффициенты mn определяют в зави - имости от условий опирания кромок по табл. 3.4.
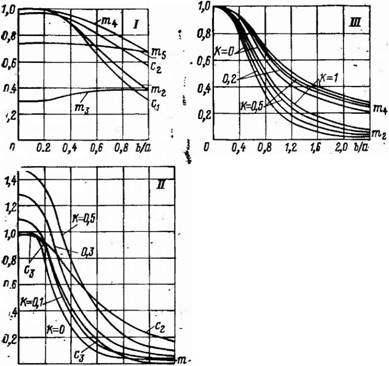
|
Рис. 3.12. Коэффициенты изгиба для прямоугольных пластин |
|
|
|
О 0,4 0,8 1,2 1JB г, СЬ/а 0 0,1 0,8 1,2 У> 2J) Ь/а |
Таблица 3.4
Изгиб прямоугольных пластин
Коэффициенты изгиба Кромки 1, 2. 3, 4 шарнирно оперты (рис. 3.11) mi=ci+kc2, ci, с2. /л2, /и3, т4 и ms по графикам рис. ЗЛ2,1 '
|
При K sЈ0,5 Mi по графикам рис 3.12. И |
|
При А>0,5 гп1=сз+ксг коэффициенты с3, с3 По графикам рис. 3.12, II |
Кромки 1, 2 шарнирно оперты, кромки 3, 4 защемлены (рис. 3.11) т2, ms, mt, ms по графикам рис. 3.12, III, IV
Б) Продольно-поперечный изгиб
Для случая действия продольных сил в направлении короткой стороны пластины (при Ь<а действуют усилия Ту, Тх—0, при а<Ь действуют усилия Тх, 7y=i0) (см. рис. 3.11) прогибы и напряжения определяют в зависимости от типа заполнителя по формулам п. 2, а. Коэффициенты тп находят по табл. 3.4.
В случае действия усилия Ту значения тп следует разделить
На ( 1------ -=г- ) • в случае действия усилия Тх значения mn делят
1 уе '
Иа / 1 —. Критические нагрузки Туе, Тхе и все параметры,
V 'же /
Необходимые для их вычисления, определяют по формулам (3.15) в соответствии с указаниями п. 1, Б § 2.
При вычислении Тхе следует использовать вторую и пятую графы табл. 3.2. При вычислении Ту следует иметь в виду, что случаю сжатия пластины, изображенной на рис. 3.11, усилиями Ту, когда кромки 1,2 шарнирно оперты, а кромки 3,4 защемлены, соответствует случай сжатия пластины,' изображенной на рис. 3.4, усилиями Тх, когда кромки 3,4 шарнирно оперты, а кромки 1,2 защемлены. Поэтому при определении Туе (см. рис. 3.11) следует использовать четвертый столбец табл. .3.2. Если Т — растягивающие силы, то во всех формулах следует изменить знак на обратный.