КОНСТРУКЦИИ С ЗАПОЛНИТЕЛЯМИ ИЗ ПЕНОПЛАСТОВ
Пластины в условиях цилиндрического изгиба
Пластину, нагруженную равномерно распределенными пг кромкам сжимающими усилиями Т, можно считать работающее в условиях цилиндрического изгиба и рассчитывать на устойчи вость по формулам настоящего пункта в следующих случаям.
•ятся также сжатые трехслойные стержни (а/5 мало). В случае стержней при определении жесткостей коэффициенты Пуассона принимаются равными нулю.
Для определения значения критической нагрузки на пластину в условиях цилиндрического изгиба необходимо сначала по формулам (3.1)—(3.6) найти жесткостные параметры панели.
Жесткость на единицу ширины панели при сжатии определяется как сумма жесткостей внешних слоев (f? i и В2) и слоя заполнителя (Дс):
B^Bi + Bz + Bc - (3.1),
|
|
ЖесйсОсть на единицу ширины панели при изгибе вычисляется как жесткость составного пакета из трех слоев относительно нейтральной поверхности пакета:
D = £>! + £>2 + £>с + BiHi. (3.2}
Здесь
Hi = h — ho, hi = h + ho,
Жесткости при растяжении (Bu В2) и при изгибе (Du £)2) на единицу ширины листа первого и второго внешнего слоя
Л - R
При сплш1ном изотропном заполнителе типа неармированного пенопласта (£0=£п)
= De—3(1 -ц*д) ' Gc = Gn - -(3<4)
При заполнителе из армированного пенопласта (рис. 3.3) жесткости В с, Dc и приведенный модуль сдвига Gc определяют в зависимости от направления ребер армировки. В случае если направление ребер армировки совпадает с направлением действия нагрузки, принимают
В 2E*h ■ п - Ex(h!+h!)
Ве = ------------------- ; 1JC ----- -------------------- —; Oe==Oxz. («3.5),
В случае если направление ребер армировки перпендикулярно к направлению действия нагрузки, принимают
|
2Eyh |
|
Вс = |
|
Dr |
|
(3.6) |
|
JVz- |
|
1 ЬхуЬух |
Ey(h - f У) 3(1 — ЦздЦу*)
- Значения Hx и Л2 определяют по (3.2). Значения приведенных модулей упругости Ех, Еу, приведенных модулей сдвига Охг, Gyz И коэффициентов Пуассона армированного пенопласта
«пределйют по формулам (3.42).
|
|
|
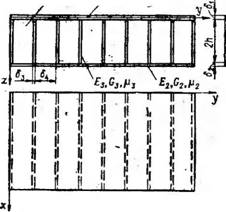
Рис. 3.3. Схема трехслойной пластины с заполнителем. из пеногласта, армированного ребрами |
В случае оболочки симметричного строения (т. е. с одинаковыми внешними слоями 61=62, В=В2, Ло=0) формулы (3.1), ,(3.2) соответственно упрощаются:
В = 2Вх + Вс; D = 2Di + Dc + 2Bl(h + ~-)*.
После определения жесткостных параметров панели вычисляют параметр сдвига K по формуле
|
(3.8) |
(3.7)
K =
2Gcb*
Здесь
В0 + + ^ Вс В2)2.
Значение критической нагрузки Те на единицу ширины панели в предположении идеализированной упругой работы конст рукции определяют по формуле
WD Te = —mt.
Оезразмерный критический параметр пц зависит от условий опирания'нагруженных кромок пластины 1,2 (см. рис. 3.2). В случае если хромки шарнирно оперты, - х
1
Mt
1-ЬА
В случае если кромки защемлены,
|
Mt |
4
1 +4А
В случае если одна из кромок защемлена, а другая свободна (консольная пластина),
В случае если одна из кромок защемлена, а другая шарнирно опёрта, mt определяют по графику рис. 3.6.
По найденному значению Те находят критические напряжения в каждом из двух внешних слоев (i=1, 2) пластины в предположении идеализированной упругой работы конструкции:
![]()
![]()
|
Ое1 — —5— ; <Те2 = ~57~' (3.9) |
Значения aei для каждого из слоев с помощью формул <3.11)—(3.13), приведенных ниже, пересчитывают в действительные критические напряжения (»=1Г 2) для каждого из слоев в зависимости, от значений предела прочности <jBf. предела пропорциональности ати а в случае явно выраженной площадки текучести— в зависимости от предела текучести an материала данного слоя (при нагреве — с учетом температуры).
. По найденным значениям Окь окг определяются действительные критические усилия на единицу ширины пластины по формулам
_ B6i
■ in = CTnl ——-,
Т В1 <310>
Тк — СГк2
02
Из двух значений Тк выбирается меньшее, которое принимается за действительную критическую нагрузку.
Если внешние слои выполнены из одинакового материала, для определения действительной критической нагрузки - достаточно расчета па одному из внешних слоев. В этом случае критическое напряжение во внешних слоях в предположении упру
гой работы конструкции рассчитывается по любой из формул (3.9). Далее производится пересчет этого напряжения по одной из формул (3.11) — (3.13). Действительные критические усилия рассчитываются по любой из формул (3.10).
В случае если внешние слои выполнены из материала, ие имеющего явно выраженной площадки текучести, действительное критическое напряжение определяется по величине аеi (i= = 1,2) с помощью одного из двух приближенных приемов:
|
1) |
|
(3.11); |
<ТкI = 1Ои (При Oei < Спад,
Ojd == ч I <Хв» — (Obi — Опц») У - ДЧ' I при Oei > Опц»; 1 ' ' Oei J
OBi
Где if { =-------- .
|
2) |
|
(3.12) |
|
0«i = TJOei |
Oei
Расчет по формулам (3.11) дает лучшие результаты (более близкие к экспериментальным) в тех случаях, когда cei<<Tm, i или Oei незначительно превосходит Опщ. Расчет по формулам (3.12) дает лучшие результаты в тех случаях, когда oei значи-. тельно превосходят Опщ.
Для материалов с явно выраженной площадкой текучести (типа мягкой стали) определяется по формулам:
Ом = TJOei Ири Oei < On,
Oki = r}0,i при Oei > <Tii.
Коэффициент tj в формулах (3.11) — (3.13) зависит от качества изготовления панелей и назначается в пределах 0,80—1,0.
Б. Прямоугольные плоские и цилиндрические панели
Порядок расчета аналогичен изложенному выше в п. А.
В случае сплошного изотропного заполнителя типа неарми - рованного пенопласта жесткости изгиба D, сжатия В панели и
|
- тят |
|
|
|
-i -» |
|
Г |
JJ IЩ t ЦП
3 d
Рве. 3.4. Схема прямоугольной трехслойной пластины при продольном сжатии в двух направлениях и сдвиге
Параметр сдвига K определяются по формулам (3.1) — (3.7). При вычислении параметра сдвига K по формуле (3.7) размер B берется в соответствии с обозначениями на рис. 3.4 или 3.5.
При расчетах цилиндрических панелей (рис. 3.5) вычисляется также параметр кривизны а2 по формуле
SfiWD • К H
Где )х — осредненное значение коэффициента Пуассона: -
В
Значения критических нагрузок Тхе, Туе, Se на единицу ширины панели в предположении идеализированной упругой работы конструкции при сжатии, сдвиге и совместном действии сжатия И сдвига определяют по формулам
ЛЮ л2D
Te = -—mu Se = — m8. (3.15)
Значения mt и т8 определяют в зависимости от условий опи - рания кромок панели и условий нагружения: в случае удлиненных панелей (^""^АО j —по табл. 3.1, в других случаях — по
В случае совместного действия сдвига и сжатия для раздельного определения пц и ms задают отношение
S-f ^
Где Т и S — расчетные значения соответствующих нагрузок.
Далее с помощью табл. 3.1 и 3.2 значения пц и ms определяют раздельно.
„ , 1 —к - При а2 ^ —, 61 = 62 и при условии, что а
^ , , ч. mt сжатой цилиндрнческои панели с шарнирно
1,73<2Л + Oi)
Опертыми кромками можно находить по формуле
M A6t . 1,73А (2ft-f-fo) .f316aV
' 0,86(2ft + 6i) 6i(l -K)+ l,73fta(2ft + 6i) ' K '
■о ел о* о. б ел л с г « е в ms
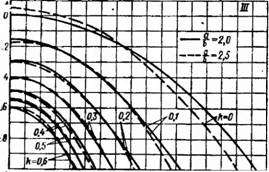
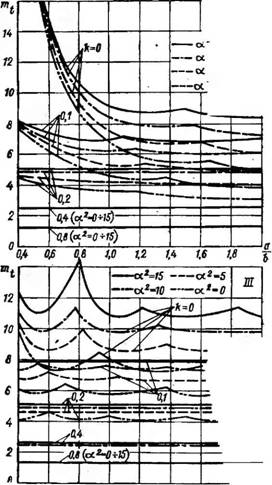
'не. 3.6. Критические ксг-ффициенты т, и Mt удлиненных плоских и ци - лин, рических панелей при продольном сжатии н при сдвиге
|
,5 %0 15 г,0 2,5 А/Ь 10 Zfi 2,5 А/Ь 1,0 1,5 Zfi 2,5 а/Ь- |
|
0,5 1,5. гр t, i А/Ь уз 1,5 г, О г,5 А/Ь 1,0 J5 "" tfi Ah |
Jhc. 3.7. Критические коэффициенты прямоугольных плоских и цилиндрических. панеле [ при продольном сжатии и при сдвиг;
|
0.8 1,8 2.4 3,2 4fi 4,в 5,6 6,4 m. |
'не. 3.8. Критические коэффициенты прямоугольных пластин при одновременном действии продольного сжатия и сдвига
|
44 46 0,8 7.0 1.2 1.4 1,6 |
|
0,4 Of ft* 1.0 1,2 1,4 Рис. 3.9. Критические коэффициенты прямоугольных рических панелей при продольном сжатии |
Действительная критическая нагрузка с учетом работы кон - струкции за пределом пропорциональности определяется так же, как опнсаио выше в п. А, путем пересчета критического напряжения, найденного в предположении идеализированной упругой работы конструкции, в действительное критическое напряжение.
В случае совместного действия на панель нагрузок Тх, Ту, S Определяется интенсивность критических усилий в предположе-- нии упругой работы конструкции. Она является исходной величиной для пересчета по формулам п. А.
Интенсивность усилий в случае совместного действия - нагрузок определяется по формуле
Т: = у Т1 + Т*уе - ТхеТуе + 3SJ. (3.17)
Значение Те* вводят далее в формулы п. А; полагая Те* = Те, Определяют меньшее из двух значений Тк согласно п. А.
Действительные критические нагрузки определяют по формулам
Тхк = фТхе, Тук = (рТуе, SK = фSe, ■ (3.18)
Тк
Где ф = —.
2. Определение прогибов и напряжений при поперечном и продольно-поперечном изгибе
Здесь приводятся формулы для'определения прогибов н напряжений трехслойных пластин с внешними слоями из различных изотропных материалов при работе в пределах пропорциональности. . . .■
А. Пластины в условиях цилиндрического изгиба.
При действии равномерно распределенной по поверхности пластины поперечной нагрузки Q или Р, равномерно распределенной по прямой, параллельной кромкам /, 2, и равномерй'6 распределенных по ширине сжимающих нагрузок Т (рис. ЗЛО)' пластина работает в условиях цилиндрического изгиба при уело1 виях, указанных в п. 1, А.
Прогибы, в середине панели (та), максимальные значения нормальных напряжений во внешних слоях и в заполнителе (а) и касательных напряжений в заполнителе (тс) определяют по формулам
B2 / 5
|
149; |
O>=s5(l8™mi + DtMl)>
6—1055
(1 ~IB) DtM>]
, Bt-T Л
+_1~ё---------- ; (ЗЛ9
D'
Тс = ~ TDtMs).
В формулах (3.19) учитывается неравномерный по толщин^ нагрев слоев пластины. Первый внешний слой имеет температ»' ру U, второй —12. По толщине заполнителя температура меняем ся линейно от ti до fc - В случае когда нагрева нет, члены фо1- мул, содержащие T в виде множителя или индекса, выпадают
При действии на пластиИу равномерно распределенной Ht грузки Q в формулах (3.19) следует принимать P0=Gb. При действии в среднем сечении пластины нагрузки Р следует принимать Ро~Р {Я — нагрузка на единицу площади; Р — нагрузка на единицу ширины пластины; Ь — размер пластины). Коэффициенты тп я Мп (п='1, 2, 3) зависят от условий нагружения и закрепления пластин и определяются по формулам, указанным в табл. 3.3 [при этом параметр" сдвига k определяют по формуле
При определении нормальных напряжений во внешних слоях tio формуле (3.19) с=<х* принимают Е0= ~ ^ ао=|(1 +
+щ)сц, ,t**tu где t= 1 для напряжений в первом внешнем слое, I—2 для напряжений во втором внешнем слое; ai, ct2, ас — коэффициенты линейного расширения материала внешних слоев и заполнителя. Значения В и D определяют по формул ау, (3.1) и (3.2).
Ж*ри определении по формуле (3.19) напряжений в заполнителе а=ас значения Е0 и ао=ю* в случае заполнителя из неармированного пенопласта определяют по формулам. £
Е0 = ———г; а* (1 + |лп)ап, Ge == G„. (3.20)
1 г - u2 *п
В случае заполнителя из армированного пенопласта при расположении ребер армировки перпендикулярно к кромкам 1, 2 (см. рис. 3.10)
Е
Е0 = -——-—, а* = а* + ЦхуОу, Gc = Gxx. (3.21)
1 — |*хуЦух
При расположении ребер армировки параллельно кромкам
Ей = --------- *------ , а* = ay -F- Ge = Gyz, (3.22)
1 —
Аз^эбз + ЬкЧпЕп Где ах = —„ _ , „ .—, ау = ап.
£303 - f - ЈnOi
Здесь ап, Еа—коэффициент линейного температурного расширения и модуль упругости пенопласта. Размеры 64, 63 показаны на рис. 3.3. ; ,
Значения Вс, Д., Ех, Еу, [х^, [х^, Gxz, Gyz вычисляют по фор - мулам (3.4)—((3.6) и согласно указаниям п. 4 этого параграфа.
В формулы для ос вводят значения температуры /^s данной точке заполнителя.
Координата точки по толщине пластины г отсчитывается в соответствии с рис. 3.10 (для крайних волокон первого внешнего слоя г=—(H+61), второго Z =Й2+Б2). В формулах (3.19) обозначено
D' = BihtHi + B2h2H2 + Д.,
2H = А1 + Л2, Hi = Hi-—Hz = + При одинаковых внешних слоях
(6i = 62, Ei = Е2, |xi = р2, ai = аг),
Dt = e[Dta* + 2{l + ]H)BiaiHlhil, (3.23)
Bt = *сР[Дса* + 2(1 + nOBiai],
H — U . __H + h
« 2A ' ---------------------- 2~
При различных внешних слоях
У /j ^ .
Z>T = о* ( • *G - LBctcp + е/?с) + ThHi + nzHfr
Bt = вса* ^ Hz 2 hl в + tcp ^ — «1 + п2,
M = (l + |ii)BiaiteAi-<cp), (3.24)
I «а = (1 + Цг) Вгаг (eft2 + *ср),
_ fe — . ________ Hhi +
2Л ' 'ср--------------- 2А-'
Значения D, В, Ви В2, Hu H2 и параметр сдвига K вычисляют по формулам (3.1)—.(3.7).
Формулы (3:19) справедливы три условиях -——— >,3,
Oi + 02
K ^ 1 при определении напряжений и K^LO при определении прогибов.