КОНСТРУКЦИИ С ЗАПОЛНИТЕЛЯМИ ИЗ ПЕНОПЛАСТОВ

ОСОБЕННОСТИ РАБОТЫ И ЗАДАЧИ РАСЧЕТА СЛОЕНЫХ КОНСТРУКЦИИ

Наиболее распространенными элементами слоеных конструк­ций являются плоские и криволинейные цилиндрические трех­слойные панёли, однослойные пластинки на подкрепляющем слое и кессоны со сплошным заполнением.

Зная особенности работы таких элементов и методику их расчета, можно рассчитать и спроектировать другие слоеные конструкции для многих практических случаев. Поэтому здесь даны сведения о работе и о расчете главным образом трехслой­ных панелей.

При проектировании и расчете слоеных конструкций, в част­ности трехслойных панелей, приходится рассматривать общую устойчивость и общий изгиб конструкции, местную устойчивость тонких элементов, подкрепленных заполнителем, прочность и жесткость заполнителя и определять оптимальные параметры слоеной конструкции.

Под потерей общей устойчивости и общим изгибом понима­ются деформации, связанные с искривлением конструкции в це­лом, в частности с искривлением срединной поверхности трех­слойной панели. Под потерей местной устойчивости понимаются деформации, связанные с местными искривлениями силовых элементов, в частности внешних слоев панели, и армирующих элементов заполнителя. Расчет заполнителя на прочность и определение оптимальных параметров слоеной конструкции свя­заны с рассмотрением как общих, так и местных деформаций.

Особенности работы и связанные с ними особенности расче­та трехслойных панелей (по сравнению со сплошными однослой­ными) определяются тем, что в маложестком легком заполните­ле могут возникать деформации, заметно влияющие на работу конструкции.

Трехслойная панель с заполнителем из весьма жесткого пе­нопласта работает так, что для нее справедлива гипотеза пря­мых нормалей. В этом случае характер работы панели мало отличается от работы обычной однослойной панели, и расчет ее на действие нагрузок, вызывающих общее искривление (напри-

.—1055
мер расчет на общую устойчивость и общий изгиб), можно в основном вести по расчетным формулам однослойной панели, вводя в них жесткости составных сечений, найденные обычными способами сопротивления материаловПри работе трехслой­ной панели с маложестким легко деформирующимся заполни­телем возникают заметные взаимные смещения внешних слоев. Это могут быть смещения взаимного сдвига внешних слоев в направлении, параллельном срединной поверхности панели, или смещения, связанные с изменением расстояния между внешни­ми слоями. Смещения могут существенно влиять на работу трех­слойной панели и делают неприемлемыми для ее расчета фор­мулы, полученные для однослой­ных панелей на основе использо­вания для всей целиком пластин­ки гипотезы прямых нормалей • (для трехслойной пластины эта ги­потеза равносильна предположе­нию об отсутствии взаимных сме­щений внешних слоев).

В каждом конкретном случае расчета панели учитывается тот или иной вид смещения. Ь одних случаях сильнее. влияют смеще­ния сдвига, в других—смещения, связанные с изменением расстоя­ния между внешними слоями.

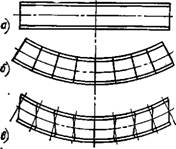
Так, при определении критиче­ских нагрузок общей устойчивос­ти или прогибов при поперечном изгибе панели весьма важно учи­тывать взаимные сдвиги внешних слоев. Это хорошо видно в двух случаях. Если модуль сдвига заполнителя бесконечно ве­лик, то взаимных сдвигов внешних слоев нет и при изгибе панель работает так, что для всей целиком пластины справедлива гипо­теза прямых нормалей (рис. 3.1, б). Если же модуль сдвига весь­ма мал, то внешние слои при изгибе панели работают по схеме, показанной на рис. 3.1, в (в пределе при модуле сдвига, равном нулю, — независимо друг от друга).

В первом случае момент инерции на единицу ширины состав­ного сечения (если учитывать только внешние слои) будет

С 3 е g

2_ i - - f - 26i (h-___ -) , во втором случае этот момент будет

1 Ниже указано, при какнх значениях параметров панели такой расчет приемлем.

2— (при 6i = 62). Так как обычно H значительно больше 61, то

Ясно, насколько велико влияние взаимных смещений сдвига внешних слоев. Для панели с реальным заполнителем, парамет­ры которого лежат между рассмотренными крайними с'лучаями, учет сдвига заполнителя существенен. Что касается взаимных смещений внешних слоев, связанных с изменением расстояния между ними, то при расчете панели на общую устойчивость и изгиб эти смещения оказывают относительно малое влияние. Таким образом, при расчете панели на общую устойчивость или изгиб должны учитываться взаимные сдвиги внешних слоев. Надо также учитывать, что на величину этих сдвигов и, следова­тельно, на величину прогиба или критической нагрузки панели сильно влияет жесткость заполнителя на сдвиг в плоскости из­гиба пластины.

При проектировании трехслойных панелей, особенно с мало­жестким заполнителем и тонкими внешними слоями, необходи­мо иметь в виду, что сжатые внешние слои таких панелей мо­гут терять устойчивость и отрываться от заполнителя. Склейка внешних слоев с заполнителем может разрушаться даже до по­тери устойчивости внешними слоями. При расчете внешних сло­ев на устойчивость или расчете прочности заполнителя и его склейки с внешними слоями внешние слои следует рассматри­вать как пластинки на упругом основании (роль основания играет заполнитель). При этих расчетах учет взаимных смеще­ний внешних слоев, связанных с изменением расстояния между этими слоями, весьма существенен. При проектировании конст­рукции следует иметь в виду, что модуль упругости заполнителя по направлению, нормальному к внешним слоям (зависящий от марки пенопласта и его армирования), оказывает сильное влия­ние на величину критической нагрузки местной потери устой­чивости.

При проектировании конструкций с армированным заполни­телем армируемые элементы следует располагать так, чтобы по­лучить повышенные значения упругих параметров заполнителя, наиболее важных для данной конструкции.

Вводя армирующие элементы, можно резко увеличить мо­дуль упругости заполнителя в направлении вдоль этих элемен­тов (при этом величина модуля в направлении, нормальном к армирующим элементам, увеличится мало). Армирующими эле­ментами в виде полосок можно резко увеличить модуль сдвига заполнителя в плоскости расположения этих полосок (при этом величина модуля сдвига в плоскостях, нормальных к плоскостям полосок, возрастет мало). При введении армирующих элемен­тов в виде проволок модуль сдвига прямоугольного элемента, стороны которого параллельны или нормальны этим проволо­кам, увеличивается мало.

5*—1055

Отсюда следует, что, например, заполнитель трехслойной пластины, опертой по двум кромкам и работающей на продоль­ное сжатие или на изгиб, целесообразно армировать полосками, нормальными к внешним слоям пластины и расположенными в плоскости изгиба пластины вдоль сжимающей нагрузки (см. рис. 2.60). Это определяется тем, что критическая нагрузка сжа­тия трехслойной пластины возрастает, а прогибы пластины уменьшаются с ростом модуля сдвига заполнителя в плоскости изгиба (нормальной к поверхности пластины и совпадающей с направлением действия нагрузки). При таком армировании су­щественно возрастут и критические нагрузки местной устойчи­вости внешних слоев, так как они сильно зависят от модуля нормальной упругости заполнителя в направлении, нормальном к внешним слоям.

Кроме армирования, определяемого соображениями расчета, целесообразно применять армирование, определяемое и конст­руктивными соображениями.

При расчете трехслойных панелей на общую устойчивость, на поперечный и продольно-поперечный изгиб решаются те же задачи, что и при расчете однослойных панелей. Однако исполь­зовать формулы расчета однослойных панелей, вводя в них вместо моментов инерции и моментов сопротивления сплошной панели соответствующие выражения для трехслойной, можно только при достаточно жестких (для заданных параметров па­нели) заполнителях. Чаще всего этот расчет следует вести по формулам, полученным для трехслойных панелей с учетом де­формаций сдвига заполнителя.

Расчет на местную устойчивость производится в случаях, когда в плоскости обоих или одного из внешних слоев действу­ют сжимающие или сдвигающие усилия и внешний слой можег терять устойчивость, как пластинка на упругом основании (роль которого играет заполнитель).

Такой расчет нужен не только для внешних слоев трехслой­ных панелей, но и для однослойных пластин с подкрепляющим слоем (см. рис. 0.1, в), стенок кессонов со сплошным заполне­нием (см. рис. 0.2), элементов армировки заполнителя и т. д.

Заполнитель на прочность следует рассчитывать во всех слу­чаях при нагружении панели нагрузками, действующими как в ее плоскости, так и в плоскостях, нормальных к поверхности панели. В случае продольного сжатия, поперечного или продоль­но-поперечного изгиба панели при определении напряжений в заполнителе и проверке его прочности необходимо учитывать напряжения, возникающие вследствие начальной волнистости внешних слоев (во всех случаях) и начальной погиби пластины (за исключением случая поперечного изгиба).

Жесткостные параметры армированных заполнителей опре­деляются расчетом в том случае, если заданы лишь параметры

Пенопласта и армирующих элементов в отдельности. Проверяет­ся также прочность и устойчивость армирующих элементов.

Оптимальные с точки зрения весовой отдачи параметры па­нели выбирают либо путем расчета ряда вариантов, либо (в от­дельных случаях) с помощью формул, позволяющих сразу опре­делять значения параметров пластины, соответствующие мини­муму ее массы при требуемой величине воспринимаемой нагрузки.

Как указано выше, конструкции с заполнителями, в частно­сти трехслойные панели, при обеспечении необходимой прочно­сти и жесткости могут давать выигрыш в массе и расходе мате­риала лишь при правильном выборе их параметров.

Если в качестве заполнителя трехслойной панели взять пе­нопласт чрезмерно большой жесткости (и соответственно боль­шой плотности), то хотя прочность и жесткость панели будут большими, панель по массе и затрате материала может оказать­ся неэффективной. Если взять пенопласт чрезмерно малой жест­кости, то может оказаться, что мала общая жесткость панели или что внешние слои будут терять устойчивость или отрывать­ся от заполнителя при малых нагрузках; таким образом, хотя масса панели за счет облегчения пенопласта и уменьшится, но эффективность ее будет низкой.

Очевидно, что для каждого конкретного случая существует оптимальная жесткость заполнителя (т. е. оптимальная для данного случая и для данного класса заполнителей плотность), оптимальное соотношение толщин внешних слоев и всей толщи­ны панели и т. д.

При оптимальных значениях параметров панели выигрыш в массе трехслойной панели по сравнению, например, с однослой­ной будет наибольшим, если этот выигрыш вообще возможен. Панели с заполнителем из пенопласта целесообразно применять - не при любых параметрах и подкреплять, например, мощные несущие слои пенопластом смысла не имеет.

В большинстве -случаев для панелей с внешними слоями ма­лой толщины и при использовании в качестве заполнителей неармированных пенопластов с точки зрения массовой отдачи панели оптимальным оказывается использование легких пено­пластов сравнительно малой жесткости. Выгодными часто ока­зываются также малые значения отношения толщины внешних слоев к толщине слоя заполнителя.

В конструкциях с весьма толстыми слоями заполнителя, на­пример "в кессонах со сплошным заполнением, целесообразно применять заполнитель с переменной по толщине плотностью, убывающей по мере удаления от внешнего слоя. Изготовление из пенопласта таких заполнителей с переменной или изменяю­щейся ступенями жесткостью возможно.

* * *

Чтобы решить задачу расчета трехслойной панели с учетом всех деформаций заполнителя, для каждого внешнего слоя и для слоя заполнителя записываются уравнения, связывающие нагрузки, действующие на слой (в том числе нормальные и ка­сательные напряжения по поверхности склейки слоев), с пере­мещениями точек, лежащих на поверхностях склейки и на кром­ках слоев. Для каждого внешнего слоя ввиду его относительно малой толщины и относительно большой жесткости материала уравнения записываются с применением гипотезы прямых нор­малей, а для заполнителя используются общие уравнения теории упругости. Далее выполняются условия равенства пере­мещений и напряжений во внешних слоях и заполнителе на по­верхности склейки этих слоев и граничные условия на контуре пластины.

Такие решения, учитывающие все компоненты напряжений в заполнителе, построены некоторыми авторами для отдельных частных случаев работы трехслойных панелей. Однако получен­ные формулы даже для этих частных случаев настолько слож­ны, что используются главным образом только для оценки точ­ности более простых приближенных решений.

Простые приближенные решения основаны на принятии не­которых упрощающих предположений, облегчающих решение и являющихся для трехслойной панели с маложестким заполните­лем более приемлемыми, чем использование здесь гипотез со­противления материалов, принимаемых при расчете однослой­ных плит.

Эти допущения не являются универсальными. Если, напри­мер, допущение о том, что расстояние между внешними слоями панели «е изменяется, справедливо при рассмотрении задач общего изгиба и устойчивости, то его нельзя принять при рас­смотрении местной устойчивости внешних слоев, так как мест­ное выпучивание внешних слоев без искривления срединной по­верхности пластины возможно только при условии изменения расстояния между внешними слоями.

Применимость допущений, использованных для получения расчетных формул, была оценена путем сравнения решений, основанных на этих допущениях, с более строгими (но и более сложными и громоздкими) решениями, проведенными без них. Установленные таким путем пределы применимости упрощен­ных формул указываются в соответствующих местах § 2 этой главы.

Укажем основные допущения, используемые при выводе ра­счетных формул.

Если толщина внешних слоев мала по сравнению со всей толщиной панели, то при рассмотрении задач, связанных с об - _цим изгиоом панели, можно пренебречь изгибной жесткостью внешнего слоя по сравнению с общей изгибной жесткостью па­нели. Пренебречь собственной изгибной жесткостью внешних слоев (т. е. принять D=D2—0)—значит пренебречь неравно­мерностью распределения нормальных напряжений по толщине внешнего слоя. Такое допущение неприемлемо при рассмотре­нии задач, связанных с местными изгибами внешних слоев (воз­никающими, например, при местной потере устойчивости). Для случаев общего изгиба оно приемлемо только в определенной области значений параметров панели.

При рассмотрении общего изгиба или устойчивости - панели можно пренебрегать влиянием сближения внешних слоев, что равносильно принятию модуля упругости заполнителя в направ­лении, нормальном к поверхности панели, равным бесконечно­сти (Ez = oo). Использование этого допущения у опор и мест действия сосредоточенных нагрузок оправдывается тем, что эти места у реальных конструкций с маложестким заполнителем всегда усиливаются дополнительными элементами.

Условия крепления кромок панели — заделки и свободного опирания — схематизируются как обычно. В частности, условие свободного опирания рассматривается как закрепление кромок пластины на мембранах, не деформирующихся в своей плоско­сти и свободно деформирующихся из нее (так называемое усло­вие свободного подвеса).

Ряд допущений связан с видом заполнителя. Различают за­полнители легкие[1], жесткие и весьма жесткие, причем каждый из этих типов заполнителей может быть как изотропным, так и ортотропным.

В связи с малой жесткостью легких заполнителей можно считать, что продольные усилия и моменты, действующие в по­перечных сечениях панели, воспринимаются исключительно внешними слоями, а заполнитель воспринимает лишь попереч­ные силы. Это равносильно принятию модулей нормальной упру­гости заполнителя в плоскости пластины равными нулю. Таким образом, легкий изотропный заполнитель рассматривают как трансверсально-изотропный заполнитель с модулями ЕХ=ЕУ = = Gxy = 0, Gxz=Gyz=Gc и в ряде случаев £2='оо. К таким запол­нителям относятся, например, неармированные пенопласты.

Легкие заполнители (например слабо армированные пено­пласты) могут быть и ортотропными. У них Gxz=^Gyz. Если Ех И Еу различны, «о малы, то можно принимать Ех=Еу=0.

Заполнитель называется жестким, если Ех и Еу настолько значительны, что усилиями, действующими в плоскости пласти­ны и воспринимаемыми заполнителем, пренебрегать нельзя. Жесткий заполнитель бывает изотропным (ЕХ=ЕУ=ЕС и Gxz= = Gyz=Gc) или ортотропным (ЕхфЕу, СХ1Ф Gyz). Если жест­кость заполнителя на сдвиг в плоскостях Xz или Yz весьма вели­ка, то в этих плоскостях можно принимать Gc = oо (что равно­сильно принятию в этой плоскости гипотезы прямых нормалей).

Заполнитель с заданными параметрами относят к тому или иному типу (легкому, жесткому и т. д.) в соответствии с преде­лами применимости расчетных формул, установленными сопо­ставлением-приближенных решений с более строгими. В ряде изданных работ для расчета панелей с легкими и жесткими за­полнителями даются различные формулы. В этой книге такие формулы даются в унифицированном виде для обоих классов заполнителей. При выводе формул отбрасываются члены малой величины.

Опыт показал, что заполнитель пластин, работающих на продольное сжатие, иногда разрушается при нагрузках, мень­ших, чем критические, соответствующие общей потере устойчи­вости пластины или местной потере устойчивости внешних слоев. Причина этого заключается в том, что реальные пластины обла­дают начальной кососимметричной погибью WK и начальной вол­нистостью внешних слоев wc, вследствие чего при нагружении пластин продольными сжимающими нагрузками. в заполнителе возникают напряжения сдвига и отрыва внешних слоев. Эти на­пряжения, суммируясь с напряжениями от сжатия пластины, мо­гут приводить к разрушению заполнителя пластины. Поэтому необходимо проверять заполнитель на действие напряжений, возникающих вследствие начальной погиби пластины и началь­ной волнистости внешних слоев.

Несмотря на то что стрела начальной волнистости внешнего слоя шс, как правило, значительно меньше4 стрелы начальной ко­сосимметричной погиби пластины шк, напряжения, возникающие вследствие этих двух начальных дефектов, могут иметь один и тот же порядок и должны учитываться.

Аналогичное положение наблюдается для трехслойной пла­стины, работающей на продольно-поперечный изгиб. Внешние слои реальной трехслойной пластины имеют некоторую началь­ную волнистость, поэтому между ними и заполнителем возника­ют дополнительные напряжения отрыва и сдвига. Эти напряже­ния суммируются с напряжениями сдвига и нормальными напряжёниями, возникающими от действия поперечных сил, изгибающих моментов и продольных нагрузок. Иногда даже при малой стреле начальной волнистости внешних слоев могут воз­никать такие дополнительные напряжения в заполнителе, кото­рые необходимо учитывать.

В некоторых случаях при расчете слоеных конструкций на общий изгиб и общую устойчивость можно частично использо­вать формулы сопротивления материалов (например, в случае весьма жесткого заполнителя, при котором справедлива гипоте­за прямых нормалей для всего составного сечения; для некото­рых конструкций с комбинированным заполнением, состоящим из конструктивных элементов и легкого. заполнителя). При рас­чете на поперечный изгиб во многих случаях можно определять формулы сопротивления материалов даже для отно­сительно легких заполнителей. Однако прогибы и критичес­кие нагрузки так определять нельзя, потому что деформации сдвига заполнителя влияют на прогибы гораздо сильнее, чем на напряжения.

Так, например, слоеная лыжа (см. рис. 2.37) на общий изгиб рассчитывалась по формулам сопротивления материалов как балка, потому что верхний и нижний внешние слои лыжи соеди­нены не только легким заполнителем, но и лонжеронами-, обес­печивающими их совместную работу. Однако такой расчет необ­ходимо дополнить проверкой местной устойчивости сжатого внешнего слоя и прочности его соединения с заполнителем. В частности, для лыжи верхний сжатый слой обшивки рассчи­тывался на местную устойчивость по формулам для слоеных панелей. Испытания лыжи подтвердили приемлемость такого расчета и необходимость расчета на местную устойчивость, так как лыжа разрушалась именно с потерей устойчивости и отры­вом верхнего листа.

При прикидочных расчетах в некоторых случаях можно при­ближенно определять напряжения сдвига в заполнителе, возни­кающие от действия поперечных усилий. В случае легкого запол­нителя эти напряжения можно считать распределенными рав­номерно по его толщине и находить их по формулам

Qxz Qyz

Txz — - ; tyZ = j——----- —,

2Л + — (61 + 62) 2Л + у(б! + б2)

Где Qxz и Qyz — поперечные силы на единицу ширины.