КОНСТРУИРОВАНИЕ И ДИЗАЙН ТАРЫ И УПАКОВКИ
Технологические расчеты тары
Технологические расчеты тары направлены на оптимизацию габаритных размеров по экономичности раскроя индивидуальных заготовок, на оптимизацию раскладки (компоновки) раскроя индивидуальных заготовок по длине и ширине листа картона формата, соответствующего размерам оборудования, производящего тару. Технологические расчеты должны включать и определение припусков на фальцовку тары.
8.7.1 .Оптимизация габаритных размеров
Для коробок, ящиков, формируемых в пространственную конструкцию методом фальцевания плоской заготовки, имеется существенная зависимость расхода материала от соотношения габаритных размеров при одном и том же объеме.
|
А |
![]()
|
Б |
![]()
|
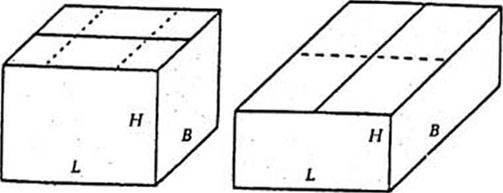
Рис. 8.61. Ящики одинакового объема с различным соотношением габаритных Размеров 2:1:2 (а), 2:2:1 (б) и 1:1:4 (в) |
![]()
|
И |
![]()
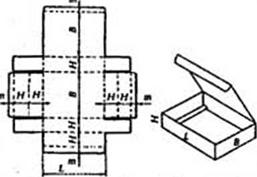
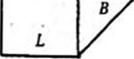 На рис. 8.61 показаны варианты ящиков одинакового объема с различным соотношением габаритных размеров. Чертеж раскроя для двух противоположных вариантов б ив ящика типа 0201 (см. рис. 8.61) приведен на рис. 8.62. Очевидно, что общая площадь поверхности этих раскроев различна. Будут различны и схемы размещения раскроев при позиционировании на листе картона требуемого формата.
На рис. 8.61 показаны варианты ящиков одинакового объема с различным соотношением габаритных размеров. Чертеж раскроя для двух противоположных вариантов б ив ящика типа 0201 (см. рис. 8.61) приведен на рис. 8.62. Очевидно, что общая площадь поверхности этих раскроев различна. Будут различны и схемы размещения раскроев при позиционировании на листе картона требуемого формата.
|
|
Ш
|
I |
![]() А
А
Рис. 8.62. Раскрой заготовок для ящиков одинакового объема с соотношением
Габаритных размеров Ь:В:Н - 2:2:1 (а) и 1:1:4 (б)
Для установления соотношения между объемом, габаритными размерами и площадью поверхности раскроя ящиков типа показанных на рис. 8.61 и 8.62 примем следующие обозначения:
1 = х В = ах-, Н = у, (8.18)
Где а = В/Ь
Учитывая, что У= ЬхВхН, из соотношений (8.18) имеем У=ах? у, (8.19)
Откуда
У= V/ ах2. (8.20)
Полная площадь поверхности раскроя (рис. 8.62) составит А = а£/2 + 4а2х2/2 + 2ху + 2аху. (8.21)
Подставим значение у из (8.20):
А = 2 ах2( 1 + а) + 2хУ/ ах2 + 2ахУ/ ах2 =
- 2 0*3(1 +а) + 2 У(1 +а)/ах. (8.22)
Дифференцируем (8.22):
ЛА/дх = 4ах( 1 +а) - 2 У( 1 +а)/ о*2. (8.23)
Минимальная площадь раскроя будет при условии
|
(8.24) |
![]() <1А/с1х = О
<1А/с1х = О
Исходя из условия (8.24) решаем (8.23) относительное 4ш:(1+а) = 2К(1 +а)/ах2,
|
(8.25) |
![]() 4а2*3 = 2 У, л3 - У/2а2,
4а2*3 = 2 У, л3 - У/2а2,
|
(8.26) |
![]()
|
2 • |
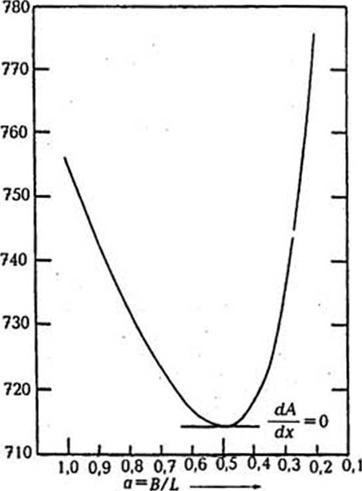
Уравнение (8.26) фактически выражает соотношение габаритных размеров при минимальной площади поверхности раскроя ящика заданного объема. Общий график зависимости (8.22) площади поверхности раскроя А (в кв. дюймах) от соотношения а для ящика объемом У= = 1000 куб. дюймов показан на рис. 8.63 [105]. Из графика видно, что
Минимальная площадь (из условия л dA/dx = 0) будет при а = 0,5. Подставляя а = 0,5 в (8.26), получаем
Для решения уравнения (8.25) по у =Н подставляем в него значение V, выраженное через у из уравнения (8.20):
Х2= соРу/2 а2 = у? у/2а} отсюда
У*= 2см3/х2 = 2олг. (8.27)
Из (8.27) следует, что при я =
=0,5 я = х.
Таким образом минимальная
Площадь раскроя картонного ящи - ^ ш зависимость площади иовсрхнос ка будет при соотношении сторон ти раскроя А от соотношения а - В/L для L : В : H “ 1:0,5:1 = 2:1:2. ящика типа 0201
Рассмотренная методика является основой для оптимизации соотношения сторон ящиков различных конструкций. Так, для стандартной конструкции ящика типа 0204 dA/dx = 0 при а - 1,0, при этом [105]:
Для а =1
L = Ж, В = aL = L, Я= V/ LB° V/L2.
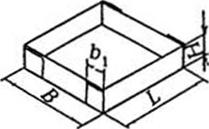
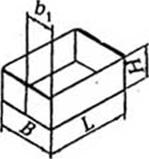
На практике такого соотношения достигнуть удается не всегда. Ящики с таким соотношением сторон обладают хорошим сопротивлением к удару (при сбрасывании ящика), но имеют слабое сопротивление сжатию. Наиболее прочным при статических и динамических нагрузках является ящик кубической формы с соотношением сторон 1:1:1, но площадь поверхности его раскроя на 12% больше. По данным ЦНИИТУ, оптимальные прочностные показатели у ящиков достигаются при соотношении сторон 1,6:1:1,25 и 1,8:1:1 [34]. Определенные по рассмотренной выше методике оптимальные соотношения габаритных размеров основных видов тары представлены в табл. 8.12 [98].
|
Со 05 |
![]() Оптимальные соотношения габаритных размеров основных видов тары из картона и гофрокартона
Оптимальные соотношения габаритных размеров основных видов тары из картона и гофрокартона
|
|||
|
|||
|
|||
|
|||
|
|
||
|
У/А |
|
= 0,397 |
|
|
|
|
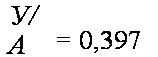 |
|
|
|
|
|
В
|
|||||||||||||
|
|||||||||||||
|
|||||||||||||
|
|||||||||||||
|
|
||||||||||||
|
Глава 8 |
|
|
|
|
|
|
|
|
|
|
![]()
|
:1 и: і г'щ £4~*-4-*4- ь 4 ^ |
|
Конструирование тары из картона и гофрокартона |
|
Коэффициенты /С, размеров сторон В |
|
Н |
|
1 |
|
= 0,794 |
|
Г2 |
|
= 1,587 |
|
¥2 |
|
1 |
|
= 0,794 |
|
Л/2 |
|
1 |
|
= 0,794 |
|
ЇІ2 |
|
= 1,587 |
|
*/2 |
|
1 |
|
= 0,794 |
|
Т. |
|
||||||
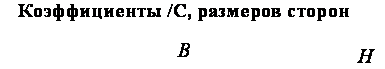 |
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
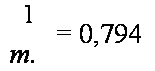 |
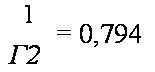 |
|||||
|
||||||
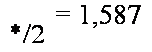 |
||||||
|
||||||
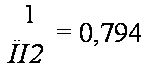 |
||||||
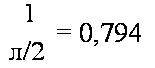 |
||||||
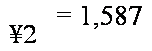 |
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|

|
= 1,310 |
|
Л/12 |
|
= 1,310 |
|
3/Ї2 |
|
1 |
|
= 0,437 |
|
^12 |
|
= 0,847 |
|
У/Ї2 |
|
= 1,310 |
|
У/12, |
|
Коэффициенты Кх размеров сторон |
|
В |
|
Н |
|
||
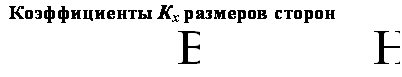 |
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
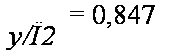 |
||
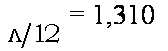 |
||
|
||
|
||
|
||
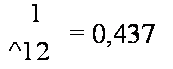 |
||
|
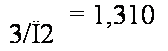 |
|
|
||
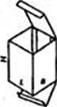
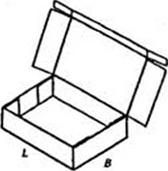
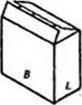
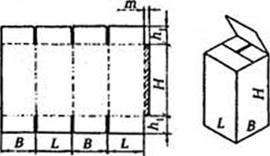
Выбор необходимого соотношения сторон ящиков следует определять с учетом всех факторов из условия оптимальности их значений. В реальных условиях размеры ящиков должны обеспечить максимальное использование площади стандартного транспортного поддона 1200x800 мм. Кроме того, при раскладке раскроя на листе картона необходимо обеспечивать соответствующую ориентацию относительно машинного направления или направления гофров у гофрокартона [25, 28].
Для упрощенного расчета количества отходов материала разработаны номограммы [78]. На рис. 8.64 приведена номограмма, позволяющая определить количество отходов картона Р (%) в зависимости от сторон ящика типа 0201. Экономическую эффективность выбора конструкции ящика обычно выражают расходом картона на единицу полезной емкости ящика.
|
-8 |
|
0,6- |
|
0,7- 0,8- 0,9 1 |
|
-5 |
|
-4 |
|
1,25- 1.5 - 2 Т |
|
Из 2 |
|
-5 |
|
X 0,9. Чч 1''. |
|
-8 |
|
0,6- |
|
||
|
||
|
||
|
||
|
||
|
||
|
||
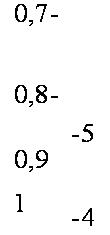 |
|
|
|
||
|
||
 |
||
 |
||
|
||
|
||
|
||
Рис. 8.64. Номограмма определения отходов материала в зависимости от соотношения
Сторон ящика типа 0201