КОНСТРУИРОВАНИЕ И ДИЗАЙН ТАРЫ И УПАКОВКИ
Общие сведения о цветовом пространстве
Из рассмотренных ранее законов Грассмана следует, что цвет можно выразить точкой в трехмерном пространстве. Трехмерное пространство для геометрического изображения цвета принято называть цветовым пространством. В нем каждому цвету будет соответствовать определенная точка, а каждой точке пространства — соответствующий цвет.
|
О |
![]()
|
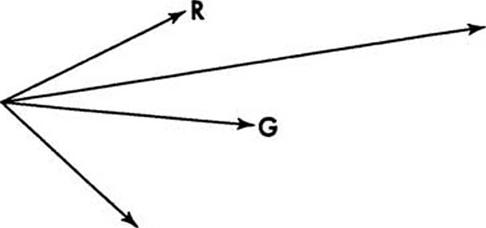
В Рис. 5.29. Вектор цвета в произвольной системе координат |
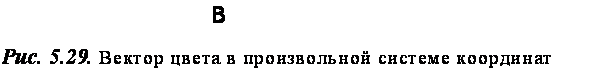
|
Ц |
![]() В цветовой координатной системе каждый цвет выражается через основные цвета этой системы. Причем, как было отмечено ранее, они должны быть линейно независимы (то есть ни один из них не должен получаться сложением двух других). Положение точки в пространстве, характеризующей тот или иной цвет, задается тремя координатами. Эту
В цветовой координатной системе каждый цвет выражается через основные цвета этой системы. Причем, как было отмечено ранее, они должны быть линейно независимы (то есть ни один из них не должен получаться сложением двух других). Положение точки в пространстве, характеризующей тот или иной цвет, задается тремя координатами. Эту
же точку можно рассматривать и как конец вектора, проведенного из начала координат в выбранной системе, например 1ЮВ (рис. 5.29).
Положение самого цветового вектора в цветовом пространстве и его длина не зависят от выбора основных цветов, а определяются цветностью и яркостью цвета. Вектор цвета любого излучения можно представить цветовым уравнением.
Для начала рассмотрим, что из себя представляет цветовое пространство на примере произвольных цветов ЯвВ (в принципе можно выбрать любую произвольную систему цветов, на рассмотрение сути дела это никак не повлияет).
|
Рис. 5.30. Вектор цвета в прямоугольной системе координат |
 Выразим некоторый цвет Ц в виде цветового уравнения. Цветовым уравнением называется уравнение, показывающее, в каких количествах нужно взять основные цвета, чтобы в результате их смешения получить цвет, зрительно неотличимый от выражаемого уравнением. Пусть в нашем случае Ц — выражаемый уравнением цвет; И, в, В — цветовые координаты цвета Ц в системе основных 1ЮВ или, иными словами, количества основных, необходимые для получения цвета Ц; К, в, В — цвета излучений, принятые за основные. Тогда, в нашем случае, цветовое урав
Выразим некоторый цвет Ц в виде цветового уравнения. Цветовым уравнением называется уравнение, показывающее, в каких количествах нужно взять основные цвета, чтобы в результате их смешения получить цвет, зрительно неотличимый от выражаемого уравнением. Пусть в нашем случае Ц — выражаемый уравнением цвет; И, в, В — цветовые координаты цвета Ц в системе основных 1ЮВ или, иными словами, количества основных, необходимые для получения цвета Ц; К, в, В — цвета излучений, принятые за основные. Тогда, в нашем случае, цветовое урав
|
Нение можно записать следующим образом:
|
Сравнив это уравнение с уравнением свободного вектора в пространстве, рассматриваемым в векторной алгебре, а = хх + у] + 2^, где Х]Л — тройка единичных векторов, легко убедиться, что они практически идентичны.
В нашем случае координаты цвета ЯСВ будут определять проекции вектора цвета на координатные оси цветового пространства. Направление координатных осей можно выбирать
Любое, но удобней принять цветовую координатную систему прямоугольной (рис. 5.30).
На первый взгляд, рассматривать цвет в виде вектора в пространстве представляется бессмысленным. И в самом деле, вопрос о том, куда направлен вектор, например, желтого цвета, выглядит довольно странным. Тем не менее в рассматриваемом цветовом пространстве ЯСВ этот вектор имеет вполне определенное направление. Если он находится в плоскости вИ и лежит ближе к оси в, то имеет зеленый оттенок, а если лежит ближе к оси II, то имеет красноватый оттенок. Таким образом, можно сказать, что направление вектора зависит от соотношения цветовых координат и характеризует цветность. Длина же самого вектора цвета зависит от суммы цветовых координат и выражает яркость. Вектор Ц соответствует цветам одинаковой цветности, но различной яркости.
В цветовом пространстве в виде вектора можно представить и ахроматические цвета. Это возможно, когда координаты цвета (в нашем случае 11СВ) равны между собой. В этом случае яркость цвета увеличивается по вектору от начала координат к концу, то есть от черного цвета через серый к белому. Этот вектор называется ахроматической осью. Соответственно чем больше значения цветовых координат, тем больше яркость цвета. По мере удаления от ахроматической оси увеличивается насыщенность цвета.
 В современной терминологии часто используются такие понятия, как треугольник цветности, диаграмма цветности, локус, цветовой охват. Что это такое, как они образуются и для чего нужны, будет рассмотрено далее.
В современной терминологии часто используются такие понятия, как треугольник цветности, диаграмма цветности, локус, цветовой охват. Что это такое, как они образуются и для чего нужны, будет рассмотрено далее.
А начнем рассмотрение этих понятий с принципа образования плоскости единичных цветов на примере системы С1Е1ЮВ.
Плоскость единичных цветов ()
(рис. 5.31), проходит через отложенные на осях координат яркости единичных значений выбранных основных цветов.
Единичным цветом в колориметрии называют цвет, сумма координат которого (или по-другому модуль цвета т) равна 1.
Поэтому можно считать, что плоскость О, пересекающая оси координат в точках Вк (11-1, в-О, В-0), Вс (11-0, С-1, В-0), Вв (11=0, в-О, В=1), является единичным местом точек в пространстве С1Е1ЮВ.
Каждой точке плоскости единичных Лс - Плоскость единичных _ цветов и образование треугольника
Цветов (2 соответствует след цветового цветности
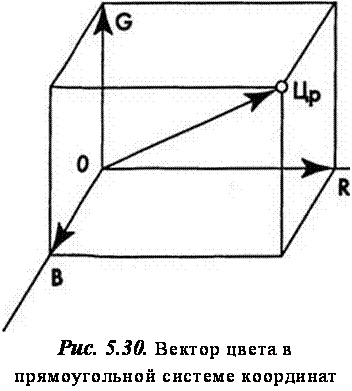
вектора, пронизывающего плоскость в соответствующей точке с тя=1. Следовательно, цветность любого излучения может быть представлена на плоскости единственной точкой. Можно себе представить и точку, соответствующую белому цвету (Б). Она образуется путем пересечения ахроматической оси (А) с плоскостью (2 (рис. 5.31).
Независимо от выбранной колориметрической системы плоскость единичных цветов, пересекаясь с координатными осями, образует треугольник, называемый цветовым треугольником или треугольником цветности (см. рис. 5.31). В вершинах треугольника находятся точки основных цветов. Определение точек цветов, получаемых смешением любых трех основных, производится по правилу графического сложения.
В колориметрии для описания цветности нет необходимости прибегать к пространственным представлениям. Достаточно использовать плоскость треугольника цветности. В нем положение точки любого цвета может быть задано только двумя координатами. Третью легко найти по двум другим, так как сумма координат цветности (или модуль) всегда равна 1. Поэтому любая пара координат цветности может служить координатами точки в прямоугольной системе координат на плоскости. В дальнейшем для рассуждений будет использована именно эта прямоугольная система.
Итак, мы выяснили, что цвет графически можно выразить в виде вектора в пространстве или в виде точки, лежащей внутри треугольника цветности.