РАСЧЕТ КОП
Глава 2 Теория тепловых насосов - содержание
В этом разделе рассмотрены типичные величины, характерные для теплового насоса, применяемого с целью восстановления тепла. Возможные показатели реального цикла связывают с показателями цикла Карно.
Предположим, что существует производство, в котором используется промывочная вода. Вода заключена в большой бак при температуре 65° С и после очистки сбрасывается при температуре
35° С. Назначение теплового насоса состоит в восстановлении тепла сбросной воды и использования его для поддержания температуры водяного бака. Временно пренебрежем возможностью частичного использования для этой цели простого теплообменника.
Максимальный КОП по Карно
КОПк = Tm/(Th—Tl)+1 = (273 + 35)/(65—35) +1 = 11,3.
Теперь рассчитаем, что можно получить на практике.
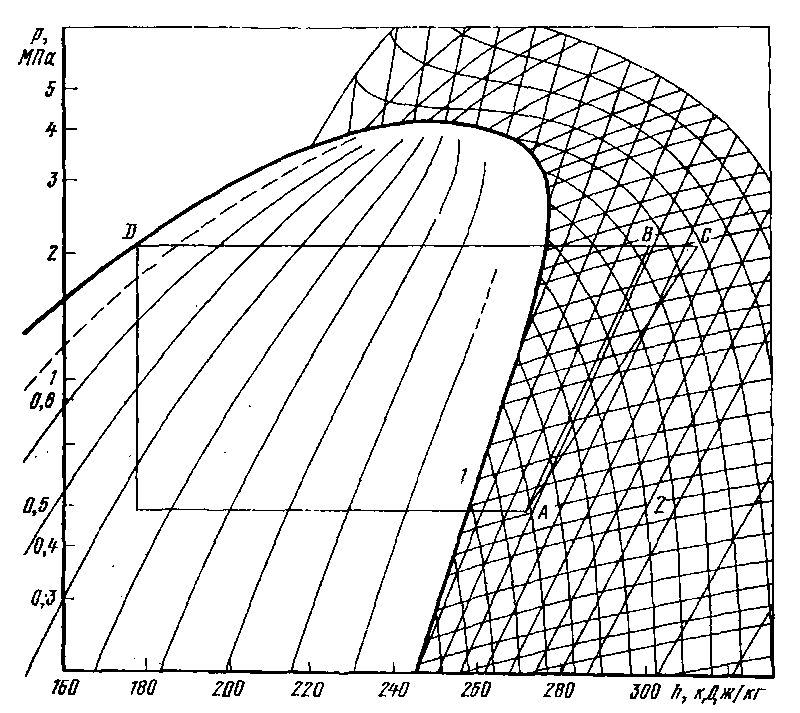
Рис. 2.7. Парокомпрессионный цикл на хладоагенте R12.
1 — линия насыщения; 2 —изотермы.
Во-первых, нужно выбрать температуры испарения и конденсации.. Они зависят от размера теплообменников, которые предполагается установить. В качестве типичных значений можно принять Tн=75°С и TL= 15° С. Отметим, что в испарителе нужна большая разность температур, поскольку сбрасываемая вода должна быть охлаждена от 35° С, до, например, 20° С, чтобы получить полезное тепло.
Затем примем в качестве рабочего тела хладоагент R12. Выбор рабочего тела, вообще говоря, дело не простое (см. гл. 3). Но в данном случае как пример выбран R12, а его р—h диаграмма
показана на рис. 2.7.
Изображение цикла всегда начинается со сжатия. Примем необходимый перегрев пара на входе компрессора 20° С и обозначим его состояние точкой А. Она находится путем продолжения линии
постоянного давления, соответствующей испарению при 15° С 0,49 МПа) до пересечения с изотермой 35° С. В точке А удельная энтальпия равна 271 кДж/кг. Проведя по изоэнтропе линию до пересечения с изобарой 2,1 МПа, соответствующей температуре конденсации 75° С, получаем условия на выходе изоэнтропического компрессора в точке В с удельной энтальпией 300 кДж/кг. Действительные условия на выходе из компрессора в точке С рассчитываются с помощью изоэнтропического КПД:
n=(hB-hA)/(hc-hA),
откуда следует, что при n = 0,7 hc — 312 кДж/кг и точка С наносится на график рис. 2.7.
Изменение энтальпии в конденсаторе и соответствующую точку D при hD=177 кДж/кг находим по пересечению изобары конденсации с левой пограничной кривой, пренебрегая при этом падением давления при теплообмене.
Для реального цикла
КОП = (hc-hd)/(hс—ha) = (312 —177)/(312—271) = 3,29.
Кроме того, следует вспомнить о механическом КПД компрессора, который потребует затраты дополнительной работы.
Полный КОП = 3,29*0,95=3,13.
В итоге для КОП получаем:
Цикл Карно 11,3
Цикл Карно с учетом теплообменников 4,8
Цикл с учетом термодинамических потерь 3,3
Цикл с учетом механических потерь 3,1
Значение этих цифр очевидно. Существенную роль играют теплообменники, поскольку снижение Дt окупает затраты повышением КОП. В этом смысле наиболее выгодным являются приложения, где используется скрытая теплота фазового перехода по обе стороны теплообменников (например, дистилляция, см. гл. 7).