КАНАЛИЗАЦИЯ

РАСШИФРОВКА ЗАПИСЕЙ ВЫПАВШИХ ДОЖДЕЙ

Рологических станций, на которых установлены самопишущие дождеме­ры, регистрирующие интенсивность и продолжительность дождей. Для расчета дождевой сети нужно в первую очередь использовать эти дан­ные при условии, если они охватывают период не менее 15 лет.

Существуют различные способы расшифровки записей дождемеров. Наиболее употребителен способ, разработанный Ленинградским научно- исследовательским институтом Академии коммунального хозяйства (ЛНИИ АКХ). Он состоит в следующем. Для каждого дождя находят максимальную интенсивность, соответствующую различным, заранее за­данным промежуткам времени (5, 10, 15, 20 мин и т. д.) в начале, середи­не или конце дождя, и устанавливают зависимость между интенсивно­стью и продолжительностью в пределах каждого дождя.

Работа по расшифровке заканчивается заполнением формы, которая характеризует весь процесс выпадения дождя (табл. 3.21).

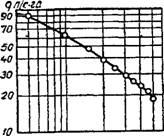
Более наглядно этот процесс может быть изображен графически с применением логарифмической сетки. В этом случае в логарифмических координатах откладывают время выпадения дождя по оси абсцисс, а интенсивность — по оси ординат и получают зависимость интенсивности дождя от его продолжительности в виде ломаной линии (рис. 3.62).

Для упрощения можно находить три-четыре характерных точки линии.

При изучении дождей, выпадающих в какой-либо местности, указан­ным способом расшифровывают запись на ленте самопишущих дождеме­ров для наиболее интенсивных дождей, и результаты расшифровки нано­сят на одну логарифмическую сетку. Это дает возможность найти зако­номерность выпадения дождей в данной местности, установив зависимость интенсивности дождя от его продолжительности при любой повторяемости дождей.

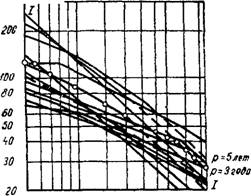
На рис. 3.63 обработанные данные о выпадении дождей за 20 лет
нанесены на логарифмическую сетку. Как уже было указано, законо­мерность каждого выпавшего дождя представлена здесь ломаной линией. Примем период однократного переполнения р — 5 годам и определим со­ответствующую ему интенсивность. Допустимое число превышений иско­мой расчетной интенсивности при дождях любой продолжительности в течение 20 лет будет равно: 20 : 5—4.

Отсчитав по графику для каждой продолжительности четыре линии сверху, соответствующие четырем дождям, интенсивность которых пре­вышает расчетную, получим на пятой линии ряд точек, определяющих расчетные интенсивности дождей, которые будут превышены в 4 раза за 20-летний период и отвечают, таким образом, принятому периоду од­нократного превышения — 5 лет.

Как видно из рис. 3.63, эти точки располагаются на линии, близкой к прямой. Уравнение этой линии, выражающее интенсивность дождя Q, Л/(с-га), в функции его продолжительности T, и даст нам требуемую за­висимость.

Для каждой точки с координатами lg T и lg Q, лежащей на линии с углом наклона а (обозначаем N — Tg а) и начальной ординатой прямой /—/ lg А (в данном случае при ^ = 5 мин), можно написать уравнение

Lgq = LgA-Nlgt, (3.54)

Откуда

Q = Ajtn. (3.55;

Величины Лип можно найти графическим способом, проводя сред­нюю линию по точкам, найденным на основании записей дождемеров, нанесенных на логарифмическую сетку, и тогда для любого значения T2 Можно определить величину Q.

Однако обычно точки не располагаются на одной прямой. Тогда ве­личины Ann можно определить по способу наименьших квадратов, поль­зуясь формулами:

2 1Gqt 2 LgTj — m2 Lg qt 1 Ціі M

Где m— число найденных точек;

Qt и Tt—интенсивность дождя, л/(с*га), и продолжительность его, мин, соответствующие найденным точкам.

Аналогичным образом можно найти величины А и п для любого дру­гого значения р.