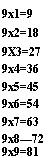ЗНАЮТ ЛИ МАШИНЫ ТАБЛИЦУ УМНОЖЕНИЯ?
Продолжая наше ознакомление с механизацией счёта, перейдём теперь к следующим двум арифметическим действиям — умножению и делению. Всякий пользуется для этого таблицей умножения, но в то же время любой школьник знает, что умножить одно число на другое — это значит сложить множимое с самим собой столько раз, сколько единиц содержится во множите - л е. Другими словами, умножение можно заменить сложением. Обычная для умножения запись 35X12 = 420 представится тогда как
35 + 35 + 35 + 35 + 35 + 35 + 35 + 35 + 35 + 35 + 35 + 35 = 420 12 раз по 35
Аналогичная картина и в делении. Его можно изобразить как последовательное вычитание делителя из делимого. Количество возможных вычитаний и явится частным.
Убедимся в этом. 420 : 35 = 12.
420— 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 — 35 —35=0
^ ____________________ шящ/тя_________________ >
35 в 420 содержится 12 раз
Исходя из этого, ясно, что на суммирующих машинах можно делать умножение и деление. Однако в действительности слишком много причин мешало «машинной математике» использовать этот приём.
Во-первых, пришлось бы многократно устанавливать на клавиатуре одно и то же слагаемое (при умножении) или одно и то же вычитаемое (при делении), во-вторых, неизбежен подсчёт в уме количества произведённых действий и, наконец, в-третьих, даже при тех больших скоростях сложения и вычитания, которые обеспечивают суммирующие машины, процесс этот протекает слишком медленно.
Выявив причины, мешавшие осуществлению на машинах умножения и деления, конструкторы, работавшие в области счётно-вычислительной техники, сразу же попытались их устранить.
Для того чтобы не тратить времени на многократную установку, были созданы конструкции, многократно передающие в счётчик однажды установленное число. Удалось избежать и подсчёта в уме количества произведённых действий, то-есть числа передач в счётчик слагаемых или вычитаемых. Эту работу взял на себя специальный счётчик.
Наконец, используя простое правило умножения на 10, 100, 1000 и т. д., удалось значительно сократить число операций сложения или вычитания. Ведь для того чтобы умножить любое число на другое, представляющее собой единицу с нулями, достаточно просто приписать к множимому соответствующее число нулей
17ХЮ=170; 17X 100= 1700 и т. д.
То же и при делении. Только там надо не приписывать нули, а наоборот, соответствующее число знаков делимого отделить запятой:
17:10=1,7; 17:100 = 0,17 и т. д.
Эту особенность удалось использовать в счётных машинах благодаря размещению счётчика на подвижной каретке. Если мы сдвинем каретку относительно установленного числа на один разряд вправо, а затем произведём передачу числа в счётчик, в последний разряд ничего не попадёт — там будет нуль. Результат окажется в 10 раз большим, чем установленное число. При сдвиге счётчика на разряд влево результат уменьшится в 10 раз.
Чтобы это было совершенно ясно, возвратимся к нашему примеру:
35 X 12 = 420*
Машина со счётчиком на подвижной каретке решит этот пример так:
I этап — передача числа в счётчик два раза 35-[-35 = 70;
II этап — передвижение каретки на один разряд вправо и передача числа в счётчик один раз. В счётчике произойдёт суммирование: 70 -(-350 = 420.
Таким образом, количество передач числа & счётчик сократилось с 12 до 3. Рисунок 9 наглядно показывает этот процесс.
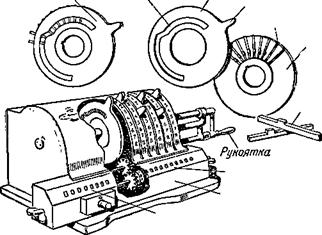
Замена умножения таким сокращённым сложением применяется почти во всех вычислительных машинах и, в частности, в арифмометре — одной из самых распространённых, самых портативных и дешёвых счётных машин. С арифмометром можно встретиться в любой бухгалтерии, в конструкторском бюро, в научной лаборатории и даже в палатках изыскательской партии, выехавшей в дальнюю экспедицию.
Арифмометр — русское изобретение. Первую машину этого типа построил ещё в 1874 году петербургский инженер
В. Т. Однер, а в 1891 году на петербургском механическом заводе он начал выпуск арифмометров своей конструкции.
Счётная машина русского изобретателя быстро завоевала признание. Принцип конструкции был немедленно заимствован иностранными фирмами. Компактность, простота в изготовлении и в использовании обеспечили арифмометрам распространение по всему земному шару. О совершенстве конструкции
|
Счётчик Езультатов Исходное положение Показания счёт - Чинов после двух передач множимого Передвижение счётчиков на один разрядвправо Показания счётчиков после новой передачи множимого |
 Установка множимого ® ©
Установка множимого ® ©
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
2 |
0 |
0 |
7 |
0 |
|
Счётчин Оборотов |
|
0 |
0 |
2 |
0 |
0 |
7 |
0 |
|
0 |
1 |
2 |
0 |
4 |
2 |
0 |
|
Рис. 9. Умножение последовательным сложением. |
Арифмометра Однера говорит тот факт, что за 75 лет своего существования она не претерпела принципиальных изменений, а количество арифмометров во всём мире превышает число всех остальных счётных машин, вместе взятых.
Заслуга Однера состоит в новаторском подходе к созданию механизма установки и передачи чисел в счётчик, выполненного в виде шестерён. Но эти шестерни, получившие по имени их изобретателя название «колёс Однера» — особые. Число их зубьев можно менять.
Для того чтобы познакомиться с колёсами Однера, взгляните на арифмометр «Феликс», выпускаемый нашими заводами. В кожухе его сделаны прорези, вдоль каждой из которых изображено 10 цифр. Из прорезей высовываются установочные рычажки. Совмещением рычажков с нужными цифрами устанавливают требуемое число.
Теперь заглянем внутрь арифмометра. Установочные рычажки оказываются выступами на диске колеса Однера. Этот диск имеет ступенчатую прорезь и примыкает к шайбе. В радиальных канавках шайбы расположены девять выдвижных зубцов. Бородки зубцов входят в ступенчатую прорезь диска. Когда мы поворачиваем установочный рычаг, чтобы совместить его с нужной цифрой, мы тем самым поворачиваем
|
Рис. 10. Арифмометр, изобретённый петербургским инженером В. Т. Однером в 1874 г. |
Диск. Ступенька в прорези диска начинает выталкивать зубцы. Число выталкиваемых зубцов точно соответствует цифре, против которой останавливается установочный рычаг.
На том же рисунке видна подвижная каретка со счётчиком, куда и надо передать установленное число. Передача числа в счётчик выполняется вращением колёс Однера, которое осуществляется с помощью рукоятки, соединённой с осью этих колёс. Поворачивая рукоятку, можно многократно передавать в счётчик однажды установленное число.
Работа арифмометра происходит в точном соответствии с рисунком 9. Для перемножения 35 на 12 нужно, установив 35, дважды повернуть рукоятку, а затем, передвинув счётчик на один разряд вправо, сделать ещё один оборот:
35 + 35 350 420
В окошке счётчика можно прочесть ответ.
Мы уже говорили о дополнительном счётчике, считающем количество передач, то-есть число вращений рукоятки (при
|
|
|
Колесо Однера |
|
Ступенчатая Диен прорезь / п |
|
1 Рычажок |
|
Радиальные канавки |
|
Шайба |
|
Выдвижные Зубцы |
|
Счётчик Оборотов |
|
Счётчик Результатов |
|
Подвижная каретка |
|
Рис. 11. Арифмометр «Феликс». Установкой рычажков в колёсах Однера выдвигают соответствующее число зубцов. При повороте рукоятки колёса Однера вращаются и передают установленное число в счётчик. |
Умножении он фиксирует множитель, при делении показывает частное). Такой счётчик есть и у арифмометра. Его называют обычно счётчиком оборотов, хотя это название нельзя считать совершенно точным. Дело в том, что счётчик оборотов показывает не суммарное число всех оборотов рукоятки, которое в нашем примере равно 3, а количество оборотов по каждому разряду множителя — 2 в разряде единиц и один в разряде десятков (12):
Как мы убедились на примере арифмометра, шестерня с переменным числом зубьев представляет собой весьма остроумное устройство.
Однако колесо Однера не исчерпывает возможных конструктивных вариантов устройства механизма установки и передачи числа в счётчик, позволяющего производить умножение и деление.
Другим распространённым вариантом механизма установки и передачи числа является ступенчатый валик.
|
Цифровое колесо / счётчика
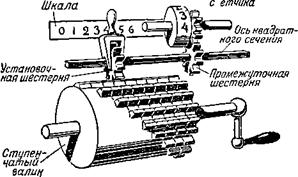
Рис. 12. Принцип ступенчатого валика. Передвижением установочной шестерни вдоль валика создают возможность зацепления её с различным числом выступов. |
Ступенчатый валик — это цилиндр, на поверхности которого имеется девять продольных выступов. Все они начинаются у одного края цилиндра, но каждый следующий выступ длиннее предыдущего на определённую величину (одну и ту же для всех выступов, например, 0,5 См).
Достаточно внимательно посмотреть на рисунок 12, чтобы обнаружить, что, несмотря на конструктивное различие, принцип работы ступенчатого валика аналогичен принципу работы колёс Однера.
В самом деле, передвигая шестерню установочного механизма до её совпадения с нужной цифрой, а затем поворачивая ступенчатый валик, мы тем самым заставляем шестерню войти в зацепление с соответствующим числом выступов валика и повернуться на тот или иной угол,
Ось, на которой находится установочная шестерня, имеет квадратное сечение, поэтому вращение этой шестерни через промежуточную передаётся цифровому колесу счётчика.
По принципу ступенчатого валика устроены автоматические вычислительные машины «Точмаш», в которых установочная шестерня передвигается от нажатия клавиши установочной клавиатуры. Для того чтобы на этой машине перемножить
|
Рис. 13. Вычислительная машина «Точмаш», устроенная по принципу ступенчатого валика. |
Два числа, достаточно установить на одной клавиатуре множимое, а на другой — множитель. Вы нажимаете клавишу умножения— и в счётчике результатов появляется произведение.
В полуавтоматической клавишной счётной машине «КСМ» ступенчатый валик с девятью выступами разной длины заменён двумя гребёнками: левая с пятью одинаковыми выступами, а правая с четырьмя выступами разной длины (рис. 14). От нажатия вилки клавиши на установочные пластины гребёнки сближаются. Величина сближения зависит от набранной цифры. Если набраны цифры 1, 2, 3 или 4, то на соответствующее расстояние сместится лишь правая гребёнка. Во время установки цифры 5 сдвигается только левая гребёнка, в то время как правая остаётся в покое. И, наконец, при установке цифр
6, 7, 8 или 9 взаимно сближаются обе гребёнки.
Между гребёнками установлена промежуточная шестерёнка, соединённая со счётчиком. При сближении гребёнок определённое число их зубцов (в зависимости от установленной
|
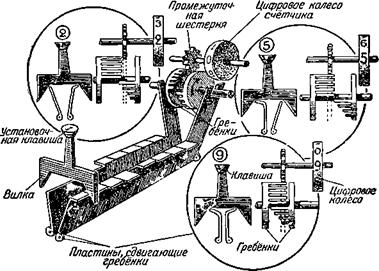
Рис. 14. Принцип счёта на машине «КСМ». Нажатием клавиши на установочные пластины сдвигают гребёнки, причём число выступоь, установившихся под промежуточной шестернёй, равно набранной цифре. Поворотом гребёнок число передаётся в счётчик. |
Цифры) становится под промежуточной шестерёнкой. Поворот гребёнок, и установленная цифра попадает в счётчик. На рисунке вверху слева мы видим передачу цифр 2, вверху справа — цифры 5, внизу — цифры 9.
Совершенно отличен от ступенчатого валика принцип пропорционального рычага, также широко применяемый в вычислительных машинах.
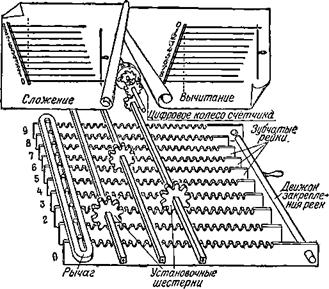
Понять его существо нам поможет рис. 16, на котором изображены 10 зубчатых реек и поперечный рычаг. Рычаг имеет прорезь, в которую входят выступы реек. А сами рейки расположены в соответствующих продольных пазах, поэтому они могут совершать лишь возвратно-поступательное движение.
Если закрепить движком нижнюю рейку и повернуть рычаг, то он увлечёт за собой остальные рейки.
Величина перемещения каждой из реек будет зависеть от её положения по отношению к центру качания рычага.
|
Рис. 15. Вычислительная машина «КСМ». |
Больше всего сместится верхняя, девятая рейка, несколько меньше восьмая и т. д. Величина перемещения будет тем больше, чем больше расстояние каждой из реек до центра качания рычага, то-есть до закреплённой рейки. Величина передвижения пропорциональна расстоянию рейки до центра качания рычага. Поэтому такой принцип конструкции и получил название принципа пропорционального рычага.
Вернёмся к рисунку. Над рейками, на квадратных осях, находятся установочные шестерни, подобные тем, какие мы видели в машине со ступенчатым валиком. Как и в предыдущих случаях, они связаны через промежуточные шестерни с цифровыми колёсами счётчика.
При наборе числа на клавиатуре установочные шестерни вводятся в зацепление с соответствующей рейкой. На рисунке показана установка числа 152. Как только рейки придут в движение, шестерни повернутся на определённые углы и передадут в счётчик установленное число.
|
Рис. 16. Принцип пропорционального рычага. Отклонение рычага влечёт за собой смещение реек, и установленное число передаётся в счётчик. |
При многократном движении реек число, установленное на клавиатуре, будет многократно суммироваться в счётчике.
Таким образом, создаётся возможность умножения на машинах с пропорциональным рычагом.
Сам процесс умножения ничем не отличается от уже рассмотренных примеров. Установленное число (множимое) передаётся в счётчик столько раз, сколько единиц содержит один разряд множителя; затем каретка со счётчиком сдвигается и опять начинается передача множимого и т. д. до исчерпания всего множителя.
Аналогично умножению произойдёт и деление. Для этого нужно закрепить не нижнюю рейку, а верхнюю, и установленное число будет вычитаться из показаний счётчика. Вычитание произойдёт путём прибавления автоматически образующегося дополнительного числа. Ведь та рейка, которая в случае сложения смещалась на одну единицу длины, теперь
|
Рис. 17, Вычислительная машина, устроенная по принципу пропорционального рычага. |
Сдвинется на расстояние в восемь раз большее, а рейки, передававшие в счётчик пятёрку и двойку, теперь передвинутся соответственно на четыре и семь единиц длины. Поэтому число 152 при закреплённой верхней рейке будет передано, как 847.
Если в счётчике у нас было 177, то произойдёт суммирование
177 847 1024
Отбросив единицу высшего разряда, мы обнаружим, что получившийся результат—24, на единицу меньше действительной разности—25, получающейся при вычитании 152 из 177. Это понятно, ибо в счётчик было передано не 848 (дополнительное к 152), а на единицу меньше—847. Недостающая единица автоматически прибавляется, а единица высшего разряда уходит за пределы счётчика.
Таким образом, весь процесс вычитания может быть представлен так:
[1]024
_1
25
Теперь, если отвлечься от схемы и учесть, что счётчик расположен в подвижной каретке и что имеется ещё счётчик оборотов, станет ясно: машина, построенная по принципу пропорционального рычага, также удовлетворяет требованиям, предъявляемым к вычислительным машинам.
На рисунках 13 и 17 показаны автоматические вычислительные машины, построенные по принципу ступенчатого валика и пропорционального рычага. Здесь не надо вращать рукоятку и передвигать вручную каретку, как это требовалось в арифмометре. Необходимое количество передач в каждом разряде и передвижение каретки осуществляются автоматически. Для этого достаточно нажать клавишу умножения или деления, и электромотор приведёт машину в действие. Электромоторный привод, облегчающий работу вычислителя, имеется у большинства современных счётных машин.
Умножение и деление на автоматических вычислительных машинах делаются со скоростью свыше 500 действий в час. Скорость —довольно большая, но людям хочется считать ещё быстрее. Существуют ли возможности дальнейшего повышения скорости? Да, существуют.
Во-первых, — это применение различных стахановских приёмов и более быстрая установка чисел человеком, обладающим достаточным навыком, а, во-вторых, применение машин прямого умножения.
Как мы убедились, умножение в вычислительных машинах делается методом последовательного сложения. Поэтому чем меньше будет количество передач установленного числа в счётчик, тем быстрее сработает машина. Поместив счётчик на подвижной каретке, конструкторы уже добились значительного сокращения числа таких передач.
Однако в машинах, с которыми мы познакомились, умножение всё же не делается прямо, за один приём. Оно требует нескольких передач установленного числа в счётчик. Количество таких передач, как нам уже известно, равно сумме цифр множителя.
Разумеется, скорость счёта была бы гораздо выше, если бы удалось создать машину прямого умножения, то-есть машину, «знающую» таблицу умножения.
О такой машине мы и собираемся сейчас рассказать. Но перед этим уделим немного внимания хорошо знакомой нам таблице умножения, напечатанной на обложках школьных тетрадей. Таблица умножения — это свод готовых произведений от взаимного перемножения цифр первого десятка. Разумеется, можно было бы не ограничиваться первым десятком и продолжить её, создав таблицу произведений однозначных чисел на двузначные, двузначных на двузначные и так далее. Пределов для такой таблицы нет, как нет их для чисел вообще. Однако, если даже ограничить эту таблицу шестизначными сомножителями, она составит миллионы томов.
Да и запомнить многозначную таблицу умножения невозможно, в то время как выучить таблицу умножения первого десятка чисел не составляет большого труда. Запомнив её, человек получает ценного помощника, так как любые многозначные числа состоят из комбинаций цифр 1, 2, 3, 4, 5,
6, 7, 8, 9, 0.
Но запомнить таблицу умножения может только человек. Память — это одно из проявлений сложных физиологических процессов, протекающих в головном мозге. Никакой машиной его не заменить. Даже самая сложная машина не обладает способностью запоминать, как это делает человек.
Однако, несмотря на отсутствие памяти, машину можно заставить вести прямое умножение, но для этого таблицу умножения надо, если можно так выразиться, овеществить.
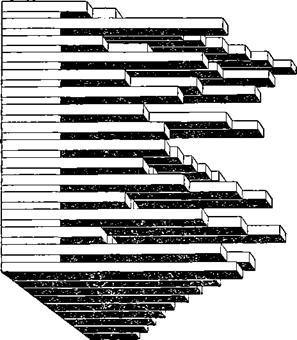
Это можно сделать по-разному. Одним из возможных вариантов являются бруски различной длины. Для выражения каждого из произведений таблицы умножения однозначных чисел достаточно двух таких брусков.
Строку таблицы умножения 3X9 = 27 можно представить в виде двух брусков: одного длиной в два сантиметра (по числу десятков произведения), второго в семь сантиметров (по числу единиц произведения). Рисунок 18 показывает, как будет выглядеть в этой системе вся таблица умножения.
|
Рис. 18. Брусковая таблица умножения. |
Машины, умножающие с помощью «брусковой» таблицы умножения, впервые были созданы ещё в конце XIX века. Они производились в России на Путиловском заводе в Петербурге. В некоторых странах они выпускаются и сейчас.
Для того чтобы понять принцип действия этих машин, необходимо вспомнить о так называемой «решётке»—старинном способе перемножения чисел, который вытеснен сейчас знакомым нам способом «столбиком». Чтобы чётко предста
вить себе умножение «решёткой», проделаем простой число* вой пример:
315
Производя это вычисление, мы рассуждаем так: девятью пять — сорок пять, пять пишем, четыре в уме. Девятью
Три — двадцать семь плюс че -
2 2 С ОМ ножи- тыре, тридцать один.
I
|
2 |
![]() Тели Этот же пример при ис -
Тели Этот же пример при ис -
Д пользовании вместо столбика
Решётки будет решаться так:
О X Л Произведение вычерчивается решетка, по сто -
3 / 1/5 — ронам которой записываются
Сомножители. Произведения
Рис. 19. Счёт «решёткой». каждой пары цифр записываются в соответствующий квадрат решётки, причём десятки отделяются диагональной чертой от единиц.
Результат получается суммированием цифр, расположенных между диагональными линиями.
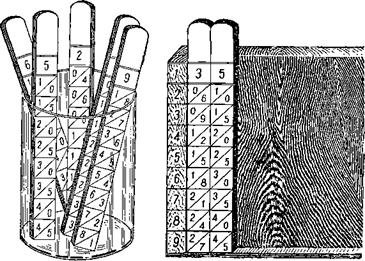
На пороге XVI и XVII веков шотландский математик Неппер упростил перемножение решёткой, предложив специальные палочки, получившие название палочек Неппер а. Каждая из таких палочек представляет собой один из столбцов таблицы умножения. На ней записан ряд готовых произведений без самих сомножителей. Сверху записан результат умножения на единицу (он же одновременно и номер палочки), затем на два, три и т. д.
Достаточно теперь посмотреть на рисунок 20, изображающий решение нашего примера с помощью палочек Неппера, чтобы убедиться в том, что с их помощью можно получить «решётку» для любых сомножителей, причём частные произведения будут уже готовы. Остаётся сложить их. Применение палочек Неппера сводит умножение к суммированию готовых произведений.
Вернёмся к машине. Каждая пара брусков таблицы представляет собой, подобно записи на палочках Неппера, десятки и единицы готовых произведений. На рисунке 21, который нам поможет познакомиться с машиной прямого умножения, изображён один из столбцов таблицы. На нём
Показаны бруски, представляющие произведения от умножения однозначных чисел на 9.
Справа от таблицы умножения находится механизм передачи чисел в счётчик. Он похож на механизм машины с пропорциональным рычагом: такие же зубчатые рейки с установочными шестерёнками на осях квадратного сечения.
|
Рис. 20. Палочки Неппера. |
Проследим за работой машины на том же примере: 35X9 = 315. Установочные шестерёнки введены в зацепление с третьей и пятой зубчатыми рейками, то-есть установлено множимое 35. Против реек множимого оказались бруски в 7 и 5 сантиметров, представляющие количество единиц в произведениях:
3X9 = 27
И
5X9 = 45.
Передвинем мысленно таблицу вправо. Бруски, встретив на своём пути зубчатые рейки, толкнут их на расстояние, соответствующее своей длине. Установочные шестерёнки на третьей и пятой рейках повернутся на соответствующие
углы и передадут в счётчик число единиц—75. Остальные рейки совершат холостой ход.
Теперь возвратим таблицу умножения обратно и одновременно сдвинем её вверх так, чтобы против третьей и пятой реек установились бруски, выражающие десятки тех же
|
9x1=9 9x2=18 9X3=27 9x4=36 9x5=45 9x6=54 9x7=63 9x8—72 9x9=81 |
|
D=b d± d=b-t±±r'
|
|
Передача единиц ~произведения |
![]()
|
0 0 7 5 0 3 15 |
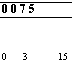 .Сдвиг счётчика Передача дест-
.Сдвиг счётчика Передача дест-
'ков произведений Суммирование
|
0 3 15 |
![]() Возвращение^чёт - " Чина в исхооное положение
Возвращение^чёт - " Чина в исхооное положение
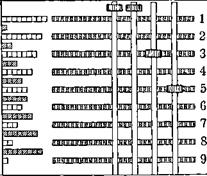
Рис. 21. Схема счёта на машине с брусковой таблицей умножения.
Произведений, то-есть бруски в 2 и 4 сантиметра, а счётчик передвинем на разряд вправо. Если таблицей опять толкнуть рейки, эти 24 десятка передадутся в счётчик и прибавятся к имеющимся там 75 единицам. Ответ готов—315. Таблица умножения и счётчик возвращаются в исходное положение.
Итак, при умножении на однозначный множитель потребовалось две передачи чисел в счётчик (передача единиц и десятков). Очевидно, что для умножения на двузначный
множитель потребуется четыре передачи, на трёхзначный — шесть и так далее, то-есть количество передач будет равняться удвоенному числу знаков множителя. В то же время мы знаем, что обычным вычислительным машинам для умножения требуется количество передач, равное сумме цифр множителя.
Теперь сравним.
Для умножения на 9 обычная машина делает девять передач, а машина прямого умножения — две; для умножения на 67 количество потребных передач будет соответственно 13 и 4. Из этих примеров видно преимущество умножения на машинах, «знающих» таблицу умножения.
Мы всё время говорили об умножении, ибо делить таким же методом, к сожалению, нельзя. Создать машину, производящую деление прямым методом, пока не удалось. Причины этого понятны.
Представив таблицу умножения в виде брусков разной длины, мы тем самым заранее определили количество десятков и единиц любого будущего произведения. Оно вытекает из заданного множителя. При делении результат определился бы величиной частного, но его-то нам и надо найти.
Неудобство при выполнении других арифметических действий, кроме умножения, послужило причиной небольшого распространения вычислительных машин этого типа. Однако принцип прямого умножения с успехом применяется в некоторых машинах более специального назначения.