ЗАКОН ПОДОБИЯ
При создании новых самолётов, кораблей, плотин, шлюзов и многих других машин и сооружений конструкторам необходимо знать, как будет вести себя проектируемый объект в условиях эксплоатации. Это необходимо для выбора наиболее целесообразных конструкций, форм, режимов работы, материалов и так далее.
Получают эти сведения испытанием моделей. Без проверки аэродинамических качеств на модели, помещённой в стремительный воздушный поток аэродинамической трубы, не начинают строить ни один самолёт. То же можно сказать и о кораблях, модели которых испытываются в специальных бассейнах, о плотинах, шлюзах и других гидротехнических сооружениях.
Сведения, полученные при испытании моделей, как правило, с достаточной точностью говорят о качествах будущей машины или сооружения. Но из этого правила есть исключения. В первую очередь это относится к тепловым системам: котлам, холодильным установкам, где обычное моделирование часто бессильно. Приходится делать опытные образцы и испытывать их. Это отнимает много времени, сил и средств. А испытать различные варианты установок зачастую вообще не представляется возможным.
Однако, кроме опыта, есть и другой путь выбора целесообразных решений. В настоящее время любой физический процесс, как бы сложен он ни был, учёные могут выразить
Математически в виде так называемых дифферен циальных уравнений.
Может быть, благодаря математическому выражению процесса отпадает необходимость в постройке и испытании моделей? Не проще ли будет решить эти уравнения и получить необходимые данные? Нет, не проще. Часто оказывается, что уравнения слишком сложны и требуют специальных математических изысканий для своего решения.
Работа может оказаться настолько огромной, что потребует много лет. Такие трудности с получением окончательного результата задерживают разрешение поставленных проблем.
Итак, ни постройка моделей, ни решение дифференциальных уравнений не могут полностью удовлетворить конструкторов и учёных.
Однако выход из этого положения был найден.
Составляя дифференциальные уравнения различных процессов, учёные обнаружили на первый взгляд странную вещь: дифференциальные уравнения, составленные для самых, казалось бы, разнохарактерных процессов, оказались одинаковыми. На эту интересную особенность указывал В. И. Ленин.
«Единство природы, — писал он в своей гениальной работе „Материализм и эмпириокритицизм“,— обнаруживается в „поразительной аналогичности“ дифференциальных уравнений, относящихся к разным областям явлений»[10]).
Академик А. Н. Крылов приводит такие примеры: «Казалось бы, что может быть общего между расчётом движения небесных светил под действием притяжения к солнцу и между качкой корабля на волнении, или между определением так называемых вековых неравенств в движении небесных тел и крутильными колебаниями вала многоцилиндрового двигателя Дизеля, работающего на корабельный винт или на электрогенератор? Между тем, если написать только формулы и уравнения без слов, то нельзя отличить, какой из этих вопросов решается: уравнения одни и те же».
Таких примеров, когда процессу в одной области физики соответствуют определённые процессы в других областях, можно привести много. Они указывают на существование в природе так называемого закона подобия.
Обнаружив в природе закон подобия физических процессов, учёные постарались применить его для решения практических задач. Но в каждой отрасли физики — свои единицы измерения: электричество измеряется одними единицами, тепло—другими, гидравлические процессы—третьими. Для сравнения на первый взгляд несоизмеримых величин был найден своеобразный масштаб, с помощью которого можно сравнивать уравнения, написанные для различных процессов. Эти масштабные коэффициенты называют коэффициентами подобия.
Теперь, имея, например, математическое выражение процесса остывания металлической отливки, можно перевести уравнение из области теплотехники в область электричества. Но почему мы выбрали именно электрическую систему? Разве решать то же дифференциальное уравнение в единицах измерения электричества легче, чем в тепловых? Нет, дело, оказывается, не в этом.
Электричеством легко управлять, а это делает возможным создание электрической цепи, в которой ток будет итти по тому же закону, что и тепло в остывающей отливке. Другими словами, можно сделать электрическую модель теплового процесса. Теперь дифференциальное уравнение можно решить..., не решая его. Достаточно произвести замеры напряжения в определённых точках модели (а электрический ток поддаётся очень точному измерению), чтобы получить график остывания отливки.
Создание электрических моделей для любых физических процессов и исследование их позволяет осуществить машина «с высшим образованием» — электроинтегратор.
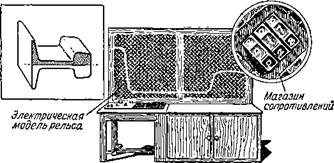
Внешний вид его показан на рис. 31. Вертикальная панель разбита на множество квадратиков, каждый из которых представляет собой магазин электрических сопротивлений. Подбирая соответствующие сопротивления, можно построить электрическую модель исследуемого явления.
Обратимся к примеру. Допустим, нам надо исследовать тепловые процессы, возникающие в железнодорожном рельсе во время движения поезда. Рельс имеет определённую форму, которую в первую очередь и надо обеспечить в электрической модели. Для этого на вертикальной панели электроинтегратора шнуром очерчивается половина контура рельса (этого достаточно, так как фигура—симметричная).
Геометрическое подобие обеспечено. Теперь внутри контура надо добиться качественного подобия, то-есть условий, соответствующих уравнению теплового процесса, протекающего в рельсе. Это достигается созданием соответствующего сопротивления в очерченной части панели. Приборами, укреплёнными на столе, задают все остальные параметры. На столе расположен также измерительный прибор, указывающий напряжение тока в любой точке модели.
|
Рис. 31. Схема электроинтегратора, созданного лауреатами Сталинской премии Л. И. Гутенмахером, Н. В. Корольковым, Б. А. Волынским и В. П. Лебедевым. |
Ток включён. Инженер наносит показания прибора для различных точек на графлёную бумагу. Соединив найденные точки, он получает график распространения тепла в рельсе при заданных условиях.
Но не только тепловые задачи можно решать на этой интереснейшей машине. Она в сотни раз ускоряет испытание различных конструкций, позволяя проверить много вариантов и выбрать лучший. Электроинтегратор сокращает время, необходимое на некоторые гидротехнические расчёты, с одного года до нескольких дней!
Широк круг вопросов, имеющих большое народнохозяйственное значение, на которые быстро может ответить машина, созданная советскими учёными Л. И. Гутенмахером, Н. В. Корольковым, Б. А. Волынским и В. П. Лебедевым, удостоенными за создание электроинтегратора Сталинской премии за 1947 год. Однако учёные не остановились на достигнутом и продолжают работу по усовершенствованию своей машины. В 1948 году коллективом, возглавляемым
Л. И. Гутенмахером, был создан образец нового электроинтегратора, в котором вместо замера значений и вычерчивания графиков на специальном экране появляются готовые кривые.
Электроинтегратор имеет свою историю. Первую в мире машину для решения сложных задач математики создал выдающийся русский учёный академик А. Н. Крылов. Большой вклад в развитие математических машин внёс профессор
Атаратура измметя Маляра Зодб/ к
|
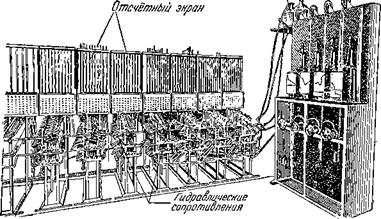
Рис. 32. Гидроинтегратор лауреата Сталинской премии В. С. Лукьянова. |
С. А. Гершгорин. Перед началом Великой Отечественной войны машин-а для решений дифференциальных уравнений — механический интегратор — была построена членом - корреспондентом Академии наук СССР И. С. Брук.
Очень интересную машину для исследования самых разнообразных процессов — г и д р о и н т е г р а т о р (рис. 32) — изобрёл профессор В. С. Лукьянов. За создание гидроинтегратора в 1951 году В. С. Лукьянов удостоен Сталинской премии.
Если электроинтегратор моделировал явления с помощью электричества, то моделирование на гндроинтеграторе происходит с помощью воды. Эта интересная математическая машина состоит, в основном, из системы сосудов различных диаметров, соединённых между собой через гидравлические сопротивления.
Различные площади сечения сосудов, система соединения сосудов между собой, гидравлические сопротивления, плавающие сосуды и другие элементы машины позволяют учитывать все заданные условия решаемой задачи и в наглядной форме — путём изменения уровней воды в стеклянных трубках отсчётного крана — воспроизводить на гидроинтеграторе исследуемый процесс.
Когда гидроинтегратор настраивается на решение определенной задачи, в стеклянных трубках устанавливаются исходные уровни воды. Их отмечают на миллиметровой бумаге, расположенной за трубками. Чтобы отразить на модели влияние каксго-либо внешнего фактора, например температуры среды, исследователь меняет высоту специальных подвижных сосудов, подключённых к машине. В результате в трубках изменяются уровни воды. В нужные моменты времени процесс приостанавливают и отмечают новое положение уровней. Затем по этим отметкам строится график протекания интересующего нас процесса.
Гидроинтегратор профессора В. С. Лукьянова даёт быстрые и точные решения дифференциальных уравнений. Важно только правильно отобразить исследуемое явление на модели, что достигается соответствующей настройкой машины.
Много разнообразных задач наглядно, быстро и точно решают гидроинтеграторы профессора В. С. Лукьянова. Среди них — исследования тепловых процессов, законов движения грунтовых вод, вопросы строительства в песках Средней Азии и в условиях вечной мерзлоты, расчёты земляного полотна железных дорог. Гидроинтегратор помогает решать научно-технические проблемы, связанные с Великими стройками коммунизма. Проектировщикам Главного Туркменского канала он определил, как будет изменяться уровень грунтовых вод в районе канала, когда потекут по нему воды Аму-Дарьи. Много других задач может быть решено на гидроинтеграторе— мощном орудии «машинной математики».