ИЗМЕРЕНИЯ и МЕРЫ

ПОГРЕШНОСТИ ИЗМЕРЕНИИ

ДЛ ы видели, что результат изме - рений никогда не бывает аб­солютно правилен. Всегда есть ка - | кие-то погрешности измерений,

| которые возникают за счёт измен-

3 чивости и неточности прибора,

Непостоянства условий (темпера­туры, влажности, атмосферного давления), а также из-за несовер­шенства наших органов чувств и неверных действий человека, про - ] изводящего измерение. Вот почему

| погрешность измерения всегда

Больше погрешности самого при­бора.

Полностью устранить погрешности невозможно. Однако их можно уменьшить до чрезвычайно малой величины. В этом и заключается одна из важнейших задач метроло­гии. Чтобы решить такую задачу, нужно разобраться во

Множестве причин, вызывающих различные погрешности; необходимо также установить классификацию погрешно­стей, то есть разбить их на несколько групп по какому - либо признаку. Вот об этом мы и поговорим сейчас. Со­вершим экскурсию... в тир.

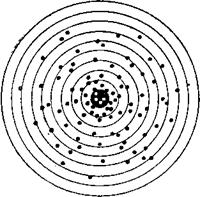
Вы стреляете по мишени, стремясь попасть в её центр. Проверим результаты вашей стрельбы (рис. 17). Попада­ния разбросаны вокруг центра мишени, причём в центре они наиболее скучены.

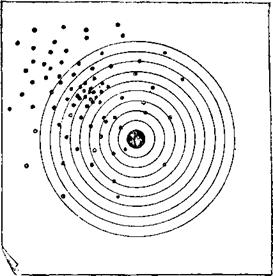
Посмотрим, как стреляет ваш товарищ. На его мишени видна совсем иная картина (рис. 18). Попадания здесь

__________________________________ ^

Рис. 17. Пример случайных погрешностей при стрельбе.

Смещены к краю мишени; место, где их больше всего, ле­жит в стороне от центра. Расстояние между точкой, куда попала пуля, и центром мишени характеризует погреш­ность стрельбы. Погрешность зависит от многого: от са­мого стрелка, от качества оружия, от силы ветра и т. д.

Если сопоставить рисунки 17 и 18, то нетрудно заме­тить различие в характере погрешностей. На мишени рис. 17 попадания расположены без видимой закономер­ности, они более или менее равномерно распределены во­круг центра. Иными словами, характер погрешностей здесь случаен, то есть они имеют множество причин. На мишени

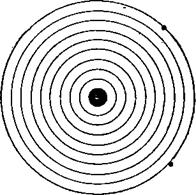
Рис. 18 следы пуль видны в стороне от центра, причём в их положении имеется определённая закономерность: стрелок систематически попадал в один и тот же край цели. Следовательно, в этом случае наблюдается уже не случай­ная, а систематическая погрешность (хотя и в этом случае есть, конечно, разброс).

Теперь взгляните ещё на одну мишень — на рис. 19. Она принадлежит плохому стрелку. Большинство «попа­
даний» у него оказалось за - рамкой мишени. Это явные промахи.

Мы познакомились с тремя видами погрешностей. Все эти погрешности могут встретиться и при измерениях.

Допустим, что, взвешивая какой-либо предмет на ве­сах, мы ошиблись в отсчёте делений шкалы и получили за­ведомо неправильный результат (например, 300 граммов вместе 500). Это типичный промах. Промах легко обнару­жить и устранить, повторяя измерение.

Представим теперь, что пружина весов ослабла. Какое бы тело мы ни взвесили на таких весах, оно всегда ока­жется «тяжелее», чем есть на самом деле. Это уже систе­матическая погрешность.

Величины систематических погрешностей характери­зуют правильность измерений. Чем меньше эти погреш­ности, тем правильнее измерения.

Но если бы нам удалось даже совершенно устранить систематические погрешности, всё равно наблюдался бы некоторый разброс результатов при повторных измере­ниях, подобный разбросу попаданий на мишени рис. 17. Этот разброс носит случайный характер и вызывается со­вокупностью многих причин, которые невозможно совер­шенно исключить, как бы тщательно ни проводилось из­мерение.

Величина случайных погрешностей характеризует точ­ность измерений. Чем меньше эти погрешности, тем точнее измерения. Влияние случайных погрешностей на резуль­таты измерений может быть учтено математическим путём с помощью так называемой теории вероятности. Её мы коснёмся в следующем разделе.