ИНЖИНИРИНГ ЗЛЕКТРОПРИВОДОВ

Взаимосвязанные системы управления

К взаимосвязанным относятся многодвигательные системы управления, связанные упругим обрабатываемым материалом (например, стан холодной прокатки, бумагоделательная машина, кордная линия и др.).

В теории и практике управления взаимосвязанными электромеханически­ми системами сложилось направление, в котором формальные процедуры оптимального синтеза одномерных или многомерных регуляторов по тем или иным критериям используются редко. Чаше стремятся получать норми­рованные динамические процессы на основе типовых алгоритмов управле­ния при малых и больших изменениях переменных с учетом совокупности всех физических особенностей технических средств, на базе которых реали­зуется электромеханическая система. Для этого посредством декомпозиции [8] взаимосвязанная система управления разделяется на сепаратные систе­мы, которые при определенных условиях можно рассматривать как квазиав­тономные. Тогда для расчета регуляторов можно использовать изложенный ранее подход.

Исследование взаимосвязанной системы управления рассмотрим на при­мере моделирования секции бумагоделательной машины [8].

Исходные данные для предварительных расчетов и исследования следу­ющие.

Параметры секций и бумажного полотна (БП): Lv = 4,2 м — расстояние между первой и второй секциями бумагоделательной машины (БД); С12 = = 2,2- 104 Н/м — коэффициент жесткости БП при растяжении между первой и второй секциями БД; г, = 0,82 м и г2 - 0,64, м — радиусы валов; ipl - 4,4 м и /Р2 = 5,4 м — передаточные числа редукторов; У, = 680 кг ■ м2 и J2 - 540 кг ■ м2 — приведенные моменты инерции агрегатов; В,2 = 800 Н/(м/с) — коэффициент внутреннего демпфирования БП.

Параметры электроприводов и датчиков систем управления секциями бумагоделательной машины: Ки1 = 40 и Кп2 = 40 — коэффициенты передачи преобразователя; Яя ц1 = 0,43 Ом и Яя и2 = 0,47 Ом — сопротивления якорных цепей электродвигателей; ТЯЛ1] = 0,016 с и Гяц2 = 0,02 с — малые постоянные времени якорных цепей электродвигателей; сд, = 4,1 Н м/А и сл2 = 4,3 Н м/А — конструктивные постоянные электродвигателей; Клт, = 0,03 В/А и Клт2 - - 0,032 В/А — коэффициенты передачи датчиков тока; Кл с1 =0,14 В/рад/с и Кйс2 = = 0,17 В/рад/с — коэффициенты передачи датчиков скорости; Ксс2 = 0,03 — коэффициент синхронизации скорости секций БД; Тп] - Тп2 - 1 ■ Ю-3 с — ма­лые постоянные времени преобразователей; тр, — постоянная времени регу­лятора тока; Гм, — малая постоянная времени контура тока; (Зр т1, (Зр,2 — коэф­фициенты усиления ПИ-регулятора тока; трс — постоянная времени регуля­тора скорости; (ЗрсЬ Ррс2 — коэффициенты усиления ПИ-регулятора скорости.

Контуры тока настроены на оптимум по модулю (трл = Тя ц, 7J„ = Тп):

W,Ap) = Рр,^^1; Рр, =——

2J

М'

В результате расчетов получим следующие значения: Ррт] = 2,87; Рр|2 = 3,672. Контуры скорости настроены на симметричный оптимум (7^, = Гм = Т„ =

_ , . - Й. і п-з

•ф. с ^ ' Ц/

Ю-3 с; тр,. = 4Г,, = 8-Ю"3 с):

= Рр. с ; РР. с=

Ър. сР ' рх 2TmcJlKXQ'

В результате расчетов получим следующие значения: Ррс, = 458,94; Ррс2 = = 202,67.

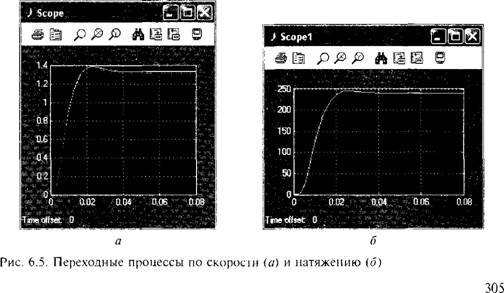
На рис. 6.4 представлена S-модель секции бумагоделательной машины, а на рис. 6.5 — соответственно переходные процессы по скорости и натяжению.

В достаточно общем виде математическую задачу оптимизации можно сфор­мулировать следующим образом: минимизировать (максимизировать) целе­вую функцию с учетом ограничений на управляемые переменные.

Математические задачи оптимизации в общем виде можно записать следу­ющим образом:

Q(a) min(max),

As U

Где Q{а) — целевая функция; U — допустимое множество, заданное ограни­чениями на управляемые переменные.

Часто для большей эффективности работы алгоритмов оптимизации в це­левую функцию (критерий качества) вводят штрафную или барьерную функ­цию. Штрафная функция равна 0, если а є £/, и быстро возрастает при удале­нии точки а і U от допустимого множества.

Разработку алгоритмов управления электромеханических систем выполня­ют, как правило, с учетом двух важнейших параметров качества:

Быстродействия (с учетом ограничений на потребляемую мощность) и свя­занной с ним производительности;

Интегральной квадратичной ошибки управления и связанного с ней каче­ства технологического процесса.

Методы формального синтеза алгоритмов управления взаимосвязанными системами и возникающие при этом сложности достаточно хорошо освещены в литературе по теории управления. Синтез оптимальных алгоритмов управле­ния локальными и взаимосвязанными системами может производиться в со­ответствии с оптимизирующими функционалами [7].

Особенностями задачи оптимизации параметров взаимосвязанных ЭП яв­ляются:

Представление исходных моделей СУ в виде сложных структурных схем с зна­чительным числом блоков, операторы которых принадлежат разным классам;

Гибкое формирование различных функционалов качества при оптимиза­ции по различным параметрам (быстродействию, энергопотреблению, точ­ности и др.);

В ряде случаев специфический, нетиповой вид оптимизируемых переходных процессов, автоматическая оценка которых общепринятыми показателями ка­чества (временем регулирования, перерегулированием и т. д.) представляет собой некоторую проблему при оптимизации по прямым показателям качества;

Предполагаемая в результате использования типовых регуляторов относи­тельно невысокая размерность пространства оптимизируемых параметров в пределах одной подсистемы ЭК.

Для оптимизации требуется применение таких программных средств, ко­торые обеспечивают достижение необходимого результата за минимальное время. Существует множество работ, в которых подробно описаны различные методы оптимизации, поэтому не имеет смысла излагать их здесь (см., напри­мер, [60]).

Выбор алгоритма оптимизации зависит от таких факторов, как точность поиска экстремума, быстродействие, условия функционирования системы, и определяется решением конкретной задачи. К группе методов для решения таких задач можно отнести методы безусловной минимизации функций мно­гих переменных и многомерной минимизации при наличии ограничений (не­линейное программирование).

Для решения поставленной задачи применяются два Toolbox: Simulink и Optimization из пакета MATLAB.

В Optimization Toolbox используются три метода для решения нелинейных задач без наличия ограничений: квази-ньютоновский, Нелдера —Мида и до­верительных областей.

Задачи нелинейной оптимизации — это комбинация неких нелинейных целевых функций, которые могут иметь линейные или нелинейные ограниче­ния. В Optimization Toolbox используется два основных метода для решения подобных задач: доверительных областей и последовательного применения ак­тивного набора задач квадратичного программирования.

Многокритериальная оптимизация предназначена в основном для мини­мизации многоцелевых функций с учетом некоего набора ограничений. В Opti­mization Toolbox реализованы два типа задач многокритериальной оптимиза­ции: задача достижения цели и задача минимакса.

Optimization Toolbox может решать нелинейные задачи методом наимень­ших квадратов, т. е. с использованием трех методов: доверительных областей, Левенберга — Марквардта; Ньютона — Гаусса.

В задачах линейного программирования целевая функция представляет со­бой некое линейное выражение, на которое могут быть наложены ограниче­ния в виде линейных равенств или неравенств. Для решения данного типа задач используются методы симплексный и внутренней точки.

Основные типы задач оптимизации, решаемых системой MATLAB Optimization Toolbox, представлены в табл. 6.6.

В табл. 6.6 приняты следующие обозначения: а — скалярный аргумент; х, у — в общем случае векторные аргументы;/(а),/(х) — скалярные функции; F(x), с(х), сед(х), K(x, w) — векторные функции; А. Аед, С, Н — матрицы; b, beq, d, f, w, goal — векторы; xL, xv — соответственно нижняя и верхняя границы области изменения аргумента.

А

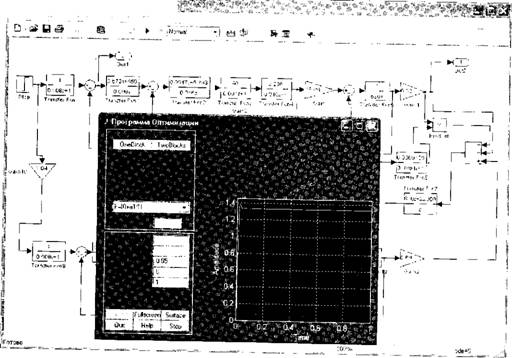
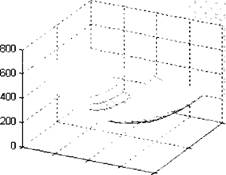
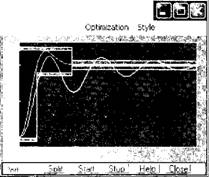
Рис. 6.6. Экранные копии интерфей­са программы оптимизации:

А — переходный процесс по скорости до оптимизации; б — переходный процесс по скорости после оптимизации; в — про­цесс поиска оптимального параметра ре­гулятора

HH9DHH1HHECD

File Edit View Insert Tools Window Help

D^SS * A ^ / & Э О

Этапу поиска экстремума функционала качества, как правило, предше­ствует подготовительная работа, связанная с созданием удобного пользова­тельского интерфейса. Это необходимо, так как напрямую методы оптимиза­ции, приведенные в табл. 6.6, использовать сложно. Примеры такого подхода к оптимизации см. в [22].

В качестве примера рассмотрим оптимизацию коэффициентов ПИ-регуля - торов скорости секции бумагоделательной машины [8] с помощью програм­мы OptSys, разработанной в СПбГЭТУ «ЛЭТИ».

Оптимизация производилась по функционалу качества, имеющему вид

/= я0/о + ah + о212,

Где а0, а2 — весовые коэффициенты; I0 = e2(t)dt, I = (de(t)/dt)2dt 12 = = (d2e{t)/dt2)2dt e(t) — ошибка по скорости.

Исходные данные для расчета и оптимизации см. в начале данного подраз­дела.

Результаты проведенной оптимизации представлены на рис. 6.6.