ИНЖИНИРИНГ ЗЛЕКТРОПРИВОДОВ

Исследование и эквивалентирование моделей, описывающих упругие механические связи электроприводов

Механизмы ЭК (бумагоделательных машин, станов непрерывной прокат­ки металла, линий по производству полимерных материалов и др.) представ­ляют собой многосвязные многомассовые механические подсистемы (ММП), управление которыми осуществляется многодвигательными системами элект­роприводов.

Чтобы с достаточной точностью отразить динамические свойства системы в заданных полосах частот сепаратных подсистем, необходимо провести ана­лиз и синтез ММП уже на этапе проектирования ЭК, поскольку внесение изменений в готовую конструкцию нерационально.

Методы математического описания и исследования характеристик ММП в общем виде рассматриваются в теории колебаний. Сложность кинематических схем основных функциональных узлов ММП ЭК затрудняет исследование их динамических характеристик. В большинстве случаев можно предположить, что взаимосвязь механической и электромагнитной систем слабая (что объяс­няется влиянием обратных связей по ЭДС двигателей на динамику СУ). Таким образом, ММП могут рассматриваться независимо от электромагнитных кон­туров управления. В этом случае входными воздействиями для ММП будут электромагнитные моменты приводных двигателей (если рассматриваются уг­ловые перемещения) или силы (если рассматриваются линейные перемеще­ния), а выходными переменными — координаты движения (скорости, угло­вые и линейные перемещения) и упругие моменты (силы). В любой ММП существуют также моменты или силы сопротивлений, которые могут быть отнесены к возмущающим воздействиям.

ММП, как и любая механическая система, может быть представлена бес­конечным числом материальных точек, упруго связанных между собой. Оче­видно, что число степеней свободы такой системы бесконечно велико и точ­ное решение задач о колебаниях подобных механических систем удается полу­чить в замкнутой форме лишь в относительно простых случаях. В общем виде эту задачу решить невозможно, что вызывает необходимость упрощения рас­четной модели ММП.

В этом случае относительно малоинерционные части ММП полагают вовсе лишенными массы и представляют в виде безынерционных элементов (жест­ких или деформируемых). Примерами таких частей ММП могут служить пере­мещаемые бумажное полотно или полоса прокатываемого металла. Наиболее жесткие части конструкции (например, направляющие, нажимные валы и др.) принимаются за абсолютно жесткие тела. В этом случае число обобщенных координат ММП будет равно числу ее степеней свободы. Как правило, иссле­дование динамических свойств ММП производится в режиме свободного дви­жения. Для чего сначала к ММП прикладывается импульс силы, а затем при отсутствии внешних возмущений исследуется движение ее к положению рав­новесия, соответствующему минимуму потенциальной энергии.

Свободное движение для устойчивой ММП всегда является затухающим под влиянием демпфирующих (диссипативных) сил. Однако учет этих сил сильно усложняет исследование динамики ММП, поэтому исследование ди­намических свойств их моделей проводится для консервативного случая, т. е. при отсутствии рассеянья запасенной в ММП энергии. Учет влияния демпфи­рующих сил возможен лишь в простых случаях или после эквивалентирования исходной модели ММП. Механическая модель ММП может быть представле­на в виде отдельных инерционных звеньев, соединенных упругими связями. Система дифференциальных уравнений, характеризующая свободные колеба­ния консервативной ММП с конечным числом степеней свободы и соответ­ствующая механической модели, является математической моделью ММП.

Подробно методика составления дифференциальных уравнений и матрич­ного описания, характеризующих свободные колебания взаимосвязанной ме­ханической подсистемы, изложена в [8].

Цр

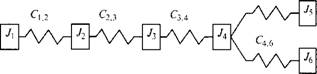
Рассмотрим определение собственных частот колебаний механической под­системы на примере электропривода клети прокатного стана 250 (см. рис. 1.4). Математические модели механической подсистемы электроприводов для 1, 3, 5, 7 клетей его черновой группы одинаковые (рис. 6.7).

Исходные данные для расчета клети 1: У, = 105000 кг - м2; J-, = 110000 кг м2; /3 = 90 кг м2; /4 = 20 кг■ м2; /5 = 100 кг• м2; Jb = 100 кг - м2; С,, = 2,8 ■ 10" Н ■ м/рад; С23 = 5,7-107 Н м/рад; С34 = 8-Ю7 Н - м/рад; С45 - 6,4-107 Н-м/рад; С46 = = 6,4-107 Н - м/рад.

Механическая подсистема электропривода клети описывается следующей системой уравнений:

■ЛФ, = С12(ф, -<р2); J2Ф2 =-Сп(фі - фг) + С2з(ф2 - Фз);

/зФз = - С23(ф2 - ф3) + С34(ф3 -ф4);

/4ф4 =-С34(ф3 - ф4) + С45(ф4 -ф5) + С46(ф4 - ф6); /5ф5 =-С45(ф4 - ф5); ЛФб =-С46(ф4 -ф6).

Расчеты собственных частот, частот упругих колебаний и собственных век­торов производим с помощью математического пакета MATLAB.

Из приведенной системы уравнений, используя методику, изложенную в [8], получим матрицу G1 для расчета собственных частот:

-С12 J1

С12 + С23 J2 - С23 J3

0

-С23 J2

С23 + С34 J3

-С34

J4

О

О

-С34 J3

-266,7 772,7 -6,3 х105 О О О

О О

-8,9х105

В MATLAB для решения задачи нахождения собственных значений матри­цы применяется функция eig. Существует несколько способов обращения к этой функции: Lam = eig(A) — столбец Lam заполняется собственными числами матрицы A; [V, D] = eig(A) — диагональная матрица D содержит собственные числа; столбцы матрицы V содержат нормированные собственные векторы для каждого собственного числа. При этом векторы нормированы таким обра­зом, что норма каждого из них равна единице.

. : 3.2844Є + 003 2.164 С

При параметрическом синтезе сепаратных систем управления взаимосвя­занных ЭП, как правило, подлежат учету лишь те частоты свободных колеба­ний ММП, которые деформируют частотные характеристики этих систем в зоне существенных частот. При инженерных расчетах достаточно учесть две - три частоты колебаний ММП, наиболее существенно влияющих на динамику работы систем управления. Для упрощения ММП производится ее эквивален - тирование двух - или трехмассовой механической системой [23, 531.

Методика эквивалентирования, позволяюшая сохранить как суммарный момент инерции (массу) ММП. так и точные значения интересующих частот свободных колебаний исходной ММП, основана на разделении главных ко­ординат исходной подсистемы на «медленные» и «быстрые» и исключении последних.

Для решения задачи эквивалентирования можно использовать алгоритм или функцию fsolve(fun, хО, options, PI, Р2, ...), входящую в ToolBox Optimization MATLAB.