Автономные системы управления
К автономным системам относятся однодвигательные системы автоматического управления, например управляемые электроприводы насосов, компрессоров, напольного электротранспорта и др.
Рассмотрим системы управления (СУ), построенные по принципу подчиненного регулирования. В этом случае синтез систем сводится к расчету регуляторов различных видов (П-, ПИ-, ПИД-, И-регуляторов и др.), контуров тока, скорости, положения и др. Для синтеза регуляторов в зависимости от требуемых динамических характеристик применяются стандартные настройки: оптимум по модулю (ОМ) и симметричный оптимум (СО), а в методах модального управления — стандартные распределения корней характеристических полиномов. Такие настройки соответствуют стабилизирующим и следящим (контурным) режимам работы систем, а также режимам параболических, треугольных и трапециидальных движений, характерных для больших изменений переменных и соответствующих пусковым, тормозным, циклическим, программно-логическим режимам работы систем электроприводов. Последнее реализуется формированием соответствующих программных заданий на входы систем управления с использованием или без использования ограничений переменных регуляторов. Подробная методика стандартных настроек и их применения изложена в [7].
После проведения синтеза регуляторов переходят к исследованию различных режимов работы автономных систем, формируя различные управляющие и возмущающие воздействия. Для этого используют матричное описание СУ или ее описание в виде передаточных функций и соответственно Control System Toolbox либо систему визуального моделирования Simulink с описанием СУ в виде соответствующих 5-моделей.
В составе Control System Toolbox можно выделить следующие основные процедуры, приведенные в табл. 6.5.
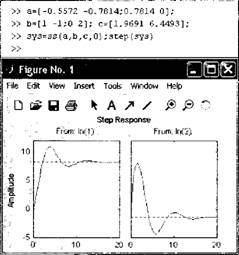
В качестве примера рассмотрим построение переходных процессов для модели СУ второго порядка (рис. 6.1).
Применение Simulink для исследования СУ будет рассмотрено в подразд. 6.2.2.
|
Процедура |
Назначение |
|
Формирование LTI-объектов |
|
|
SS Zpk tf |
Создание модели пространства состояния Создание модели нули —полюсы —коэффициенты (НПК) Создание модели передаточной функции |
|
Извлечение данных |
|
|
Ssdata Zpkdata Tfdata |
Извлечение матриц пространства состояния Извлечение данных о нулях, полюсах, коэффициенте передачи Извлечение числителя (числителей) и знаменателя (знаменателей) передаточной функции |
|
Характеристики модели |
|
|
Class і set isdt issiso isa |
Получение данных о типе модели ('ss', 'zpk' или 'tf) Проверка, является ли модель непрерывной Проверка, является ли модель дискретной Проверка, имеет ли модель один вход и один выход Проверка, является ли LTl-объект моделью заданного типа |
|
Преобразование вида модели |
|
|
C2d d2c d2d |
Переход из непрерывного времени в дискретное Переход из дискретного времени в непрерывное Изменение периода дискретности, задание запаздываний по входам |
|
Анализ динамических свойств систем |
|
|
Pole Eig Tzero Pzmap Degain Damp |
Определение полюсов системы Определение собственных значений и собственных векторов Определение нулей системы Расположение полюсов и нулей систем Нахождение коэффициента передачи при нулевой (низкой) частоте Определение частоты собственных колебаний и демпфирования по полюсам системы |
|
Процедура |
Назначение |
|
Модели пространства состояния |
|
|
Rss, drss canon ctrb, obsv minreal mod red |
Генерирование случайных моделей пространства состояния Получение канонической формы пространства состояния Получение матрицы управляемости и наблюдаемости Минимальная реализация и сокращение нулей и полюсов Редукция состояния модели |
|
Временные характеристики |
|
|
Step impulse initial lsim |
Получение переходной функции системы на единичный скачок Получение переходной функции системы на единичный импульс Реакция на начальные условия для моделей в уравнениях состояния Моделирование системы при произвольном входном воздействии |
|
Частотные характеристики |
|
|
Bode nyquist freqresp margin |
Построение диаграммы Боде частотного отклика (АЧХ и ФЧХ) Построение диаграммы Найквиста Получение частотных характеристик системы Определение запасов устойчивости по фазе и амплитуде |
|
Классические методы синтеза систем управления |
|
|
Rlocus rlocfind Place estim destim reg |
Получение корневого годографа Определение коэффициентов усиления по заданным корням характеристического многочлена Вычисление матрицы обратной связи по заданным полюсам Вычисление коэффициента передачи наблюдателя Построение дискретного фильтра Кальмана Формирование регулятора в виде обратной связи по состоянию и наблюдателя |
Для оптимизации параметров регуляторов СУ можно использовать два подхода: блоки пакета Nonliner Control Design (NCD) и возможности пакета Optimization [22].
Пакет NCD содержит три блока: CRMS, DRMS, NCD Output. Блок NCD Output является основным блоком и позволяет в интерактивном режиме выполнять следующие операции: задавать требуемые ограничения во временной
Области на любой сигнал оптимизируемой системы; задавать параметры, подлежащие оптимизации; задавать неопределенные параметры; проводить параметрическую оптимизацию системы с учетом заданных ограничений.
Рассмотрим оптимизацию параметров ПИД-регулятора, используя файл ncddemol с демонстрационным примером, входящий в состав пакета MATLAB.
|
Рис. 6.1. Пример построения переходных процессов модели системы управления второго порядка |
Задача оптимизации следующая: при заданной структуре объекта управления и известных неопределенностях его параметров найти значения коэффициентов кп, ки и кд регулятора, при которых в представленной замкнутой структуре переходный процесс будет иметь требуемые параметры.
(л! ncddemol *
File Edit View Simulation Format Tools Help
D Q? В @ mo. . I ► » iNormaT
|
Controller |
IVv— [ NCD loutPort 1 |
|||
|
PID |
И у |
|||
|
Plan |
T & Actu |
|
NCD_Outport1 Ode23 |
|
Step < Re< 100% |
И ncddemol/Plant & Actuator1
File Edit View Simulation Format Tools Help
|
Normal |
|
БОгЗ+аг.^+зІ s+1 |
□ о? в @ : m. ►
Actuator Model
0 >ffl
Limit Rate
Ode23
Рис. 6.2. Моделирование ПИД-регулятора:
A — модель объекта управления, ПИД-регулятора и NCD-блока; б — содержимое блока Plant & Actuator
При оптимизации параметров ПИД-ре - гулятора рассматриваются следующие параметры переходного процесса: длительность, время нарастания, максимальное перерегулирование, максимальное «недорегулирова - ние», начальное и конечное время моделирования, начальное и желаемое конечное значения выходного сигнала.
Объект управления представляется следующим звеном [22]: W(p) = 1,5/(50р} + а^р2 + + ар+ 1), где коэффициент а2 может принимать значения в диапазоне 40...50 (номинальное значение сь = 43), а коэффициент ах — в диапазоне 0,5... 3,0 (номинальное значение й] = 1,5).
Модель СУ представлена на рис. 6.2, а результаты оптимизации на рис. 6.3.
В результате получены следующие оптимальные коэффициенты ПИД-регу - лятора: кп = 1,34, ки = 0,15 и = 8,33.