Инфракрасные системы «смотрящего» типа

ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ

Рассмотрим кратко основные законы излучения, которые необходимо знать при расчете ИКС.

Закон Кирхгофа. В точке поверхности теплового излучателя при любой темпера­туре и любой длине волны спектральный коэффициент направленного излучения для заданного направления равен спектральному коэффициенту поглощения для противо­положно направленного неполяризованного излучения. Иначе говоря, чем больше энер­гии поглощает тело, тем больше оно ее излучает:

^^еХ2^Х2 ■ • ■ А//с^„/(Хуп Л^^чт,

Где Мйхчт - спектральная плотность энергетической светимости черного тела; ах - спек­тральный коэффициент поглощения.

В соответствии с законом сохранения энергии для любого тела ах + р*. + Тх = 1, где рх и т% - коэффициенты отражения и пропускания соответственно. Поэтому ах= 1 - рх для непрозрачных тел с = 0, т. е. по закону Кирхгофа тела с хорошей отражательной спо­собностью являются плохими излучателями.

Если в среде с постоянной по всей ее толще температурой распространяется излуче­ние с постоянной плотностью Мех, то и на выходе такой среды сохраняется то же зна­чение плотности. Если же в среде имеет место градиент температур, пропорциональ­ный распределению Мех, то плотность светимости на выходе слоя толщиной Дх равна Мех = (Д Мех /Дх)/ах + МеХ, где АМ^/Ах - градиент Мех ах - коэффициент поглощения среды; Мео - плотность излучения на входе в среду.

Закон Стефана-Больцмана. Энергетическая светимость черного тела пропор­циональна четвертой степени абсолютной температуры:

Ме = оТ (2.4)

Где ст = 5,66971-10-8 Вт-м~2-КГ^ - постоянная Стефана-Больцмана.

Для любого излучателя Мех = £>.тМачт, где гхт - спектральный коэффициент излуче­ния данного тела. Для серого тела е^т =/(Т) = ех Мест = втсГ4.

Закон Планка. Он описывает распределение энергии по спектру длин волн:

Мех = Ме(К Т) = С1Г5[ехр(С2а7) - 1] -1, (2.5)

Где С] = 3,7415-10“16 Вт-м2; С2 = 1,43879-10“2 м-К. При КГ < 3000 мкм-К для практиче­

Ских расчетов формулу (2.5) можно представить в виде

МеХ = С^ехрС-САГ). (2.6)

Закон Планка позволяет рассчитать энергетическую светимость черного тела МАХ, а

Следовательно, и поток его излучения, приходящийся на заданный или выбранный спектральный диапазон ДА = А2 - А^ Для этого можно проинтегрировать выражение (2.5) в пределах А1...А2 (см., например, табл. 2.2).

Иногда удобно вместо такого интегрирования разбить диапазон ДА на п участков и воспользоваться приближенной формулой

Ма » §Г Г‘ |Ё ^1« )’ + )' + & А. + б]ехр(-< )|,

Где А„ - значение длины волны в середине каждого участка.

Из формулы для закона Планка можно получить выражение для закона Стефана- Больцмана. Действительно, если проинтегрировать (2.5) в пределах О...оо, то получим

(1.4) , т. е.

Оо

Л/, = |маА = оГ.

О

Закон Голицына—Вина. Если задаться целью определить длину волны излучения, соответствующую максимуму кривой Мсх =/(А), т. е. найти экстремум функции Л/ел, то получим

Ашах = 2898/Г. (2.7)

Здесь Л-пах измеряется в микрометрах, а Т - в кельвинах. На практике часто это выраже­ние, называемое законом Голицына-Вина, используют в следующем виде:

Кшх = 3000/г.

Закон Голицына-Вина указывает, что с увеличением температуры излучателя мак­симум излучения сдвигается влево по спектру длин волн А, поэтому он называется так­же законом смещения.

Интегрируя выражение для МсХ в пределах 0...^*, получаем

Т. е. в коротковолновой части своего спектра черное тело излучает одну четверть всей энергии, а ее основная доля приходится на более длинные волны.

Для некоторых практических применений важно учитывать, что 50% полного излу­чения (площади кривой Планка) содержится в диапазоне 0...\/2, где А.1/2 = 4110/Г.

Чувствительность приемников излучения в большей степени зависит от скорости прихода квантов излучения, чем от энергии излучения. Поэтому можно привести вы­ражение для числа квантов излучения (фотонов), испускаемых тепловым излучателем в единицу времени и приходящихся на единичный спектральный интервал внутри полу­сферического телесного угла. Это выражение легко получается из (2.5) делением его на величину, определяющую энергию одного фотона Ед = Лсо/А. = 1,9863-10" 19/Я, (Втс):

NчX = 2л:с0Х~4 {ехр[/гс0 /(&ХГ)]-1} 1.

Поскольку мгновенная скорость излучения фотонов обусловлена многими случай­ными процессами, целесообразно оценить их влияние, приводящее к флуктуациям чис­ла Ыф через спектр шума ф9, который является зависимостью среднего квадратическо­го отклонения мощности от частоты или числа фотонов от их средних значений. Рас­сматривая мощность излучения Фе как флуктуирующую величину, можно получить:

SHAPE \* MERGEFORMAT

Ф9 = 8АкоТ5,

Где А - площадь излучателя; к = 1,3806-10-23 Дж-К1; ст = 5,6697* 10-8 Вт-м_2-К^ Для спектра шума, описывающего флуктуации числа фотонов Л^.,

Ф^=4,17-10ИЛГ3.

МеХ

Т = 320 К

X Рис. 2.10. Кривые Планка: Т]>Т2> Тъ

Черного тела с разной температурой

Для источников в виде серых тел правые части (2.9) и (2.10) следует умножить на коэф­фициент излучения.

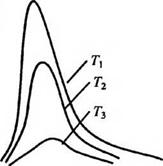
Формулу Планка можно представить графически в виде так называемых кривых Планка (рис. 2.10). Рассматривая их для каких-либо температур, можно заметить, что чем больше температура, тем выше расположена кривая, т. е. на любом участке спектра полный излуча­тель с более высокой температурой дает большую энергию излучения, чем полный излу­чатель с меньшей температурой.

В виде кривых Планка можно показать и зависимость плотностей излучения в фотон­ной форме от длины волны (рис. 2.11).

Для упрощения расчетов, связанных с использованием кривых Планка, удобно рас­сматривать единую изотермическую кривую, получаемую заменой в формуле Планка переменных А и МеХ новыми переменными:

Х = ААгоах; У = М^/М^ .

При этом формула Планка принимает следующий вид:

У = 142,32* 5 [ехр(4,965/х)-]

Чтобы от единой изотермической кривой (рис. 2.12) вернуться к кривой Планка для данной температуры Т в кельвинах, необходимо определить: 1) = 2898/Т, мкм;

2) М = 1,2864- 10“15Г5 Вт-см "2-мкм_1; 3) х = А/Апих для выбранных значений А; 4) у по

^•ти

Единой изотермической кривой или из специальных таблиц (см., например, [51]); 5) М =М у, соответствующее каждому значению А.

Если из всей энергии, испускаемой тепловым излучателем и определяемой величи­ной Ме, используется лишь ее доля, излучаемая на некоторой рабочей длине волны, то для практических целей важно знать температуру, при которой наиболее эффективно используется мощность излучателя. Определяя эффективность излучения через отно­шение функции Планка Ме(А, Т) к суммарной энергетической светимости Ме

М,(КТ).. <У[ехр(СгАГ)-1)-'

М, аТ'

И находя экстремум этого отношения, получаем,

АэфГэф = 3625,

Т. е. для данной длины волны Аэф существует определенная температура Гэф, обеспечи­вающая наибольшее отношение Ме(Аэф, Ту$)!Ме. Важно отметить, что значение Аэф не совпадает со значением Атах, рассчитываемым по (2.7).

На практике часто необходимо определить небольшую разность температур двух чер­ных тел или близких к ним излучателей. Изменению температуры Т соответствует измене­ние МеХ. Дифференцируя формулу (2.5), можно получить значение еМ^ШТ при А Г« С2:

__ МЛС2 (1Т хт[1] ’

А отсюда, перейдя к конечным приращениям, найти искомую величину

Л г 1Т2 Л л./

АТ =--------- ДМ, ,

М*С2 еХ’

Где Мсх определяется из (2.5) или (2.6).

Полезно отметить, что для длин волн, много больших ХтаХ, спектральная плотность из­лучения Мех увеличивается пропорционально Т, а в области Аяв* - пропорционально Г5.

Для оценки работоспособности многих ИКС необходимо знать выражение для кон­траста объекта, наблюдаемого на фоне. В случае объекта и фона - черных тел с темпе­ратурами Г0б и 7ф контраст в спектральном диапазоне АХ может определяться по сле­дующей формуле:

{Н*(^)/<*>-]А- §сШ^)Мк]<П.

О__________________________________

}[^Л(ГЛ)/Л]л+ }[ймл(гф)/<й]<й

А). Ак

Расчет значений КАх для диапазонов 3...5 и 8...14 мкм показывает, что в области температур фона 7ф = 240...320 К при небольших перепадах АТ = Г0б - 7ф контрасты в диапазоне 3...5 мкм больше контрастов в диапазоне 8... 14 мкм.

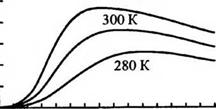
Если эффективность работы ИКС определять по значению контраста между наблю­даемым объектом и фоном, на котором он находится (объект и фон принимаются за черные тела с близкими температурами), то важно знать длину Л. с, при которой ско­рость изменения функции Планка при изменениях температуры максимальна. Для ее определения нужно найти максимум зависимости (1Ме/<1Т, который на основании зако­на Планка имеет место при ХсТ= 2411, т. е. Хс = 2411 /Т (рис. 2.13). В большинстве прак­тических задач при этом следует учитывать также пропускание среды и спектральные коэффициенты излучения объекта и фона.

Необходимо помнить, что контраст между объектом и фоном часто зависит не только от их излучательных свойств, обусловленных плотностями Мех и коэффициентами излучения, но и от коэффициентов отражения объекта и фона, если сигналы, приходящие на вход ИКС, представляют собой совокупности собственного и отраженного излучения.

При изменении температуры или переходе от светлого времени суток к темному вклады собственной и отраженной составляющей излучения могут изменяться, а отсю­да может изменяться и знак контраста. Важно учитывать, что для типовых значений

240.. .300 К температурный контраст в длинноволновом ИК-диапазоне составляет доли процента. Это, в частности, требует весьма высокой однородности чувствительности отдельных элементов приемника излучения ИКС при наблюдении или обнаружении объектов с температурами, близкими к температурам окружающих их фонов, так как такие элементы должны чувствовать малые перепады температур по площади объекта или между объектом и фоном. Допуск на неоднородность чувствительности (в относи­тельных единицах) должен быть заметно меньшим, т. е. порой составлять сотые доли процента.