Инфракрасные системы «смотрящего» типа
ВЫБОРКА СИГНАЛА И ЕЕ ВЛИЯНИЕ НА ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ ИНФРАКРАСНЫХ СИСТЕМ
Практически в любой ИКС происходит выборка отдельных значений непрерывного аналогового сигнала, т. е. преобразование его в дискретную форму. В ИКС «смотрящего» типа пространственную выборку изображения выполняет многоэлементный приемник излучения. Необходимое число выборок изображения очень часто определяется из условий выполнения требований к разрешению обнаруживаемых или наблюдаемых объектов, например, в соответствии с критериями Джонсона (см. §4.3).
Выборку изображений можно проводить с различной периодичностью по каждой из ортогональных осей системы координат (х, у), в которой рассматриваются изображения. На практике эта так называемая асимметричная выборка чаще встречается в ИКС со сканированием, хотя используется и в ИКС «смотрящего» типа. Такое название выборки связано с несимметричными аберрациями оптических систем (астигматизмом, дисхорсией), перспективными искажениями изображений для разных углов визирования, неизотропными формами чувствительных элементов МПИ и закономерностями расположения этих элементов по общей площади МПИ и др.
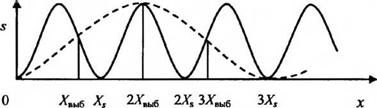
Рассмотрим простейший случай, когда исходный сигнал 5 имеет вид последовательности синусоидальных импульсов с периодом Х8 и частотой / (рис. 9.2) и подвергается выборке с периодом Хшъ и частотой /выъ//5. Легко видеть, что показанная на рис. 9.2 штриховой линией огибающая выбранных значений исходного сигнала, которая и является реконструируемым сигналом, имеет меньшую частоту, чем
В реальных системах выборка двумерных сигналов - изображений пространства предметов - осуществляется не в отдельных точках плоскости изображений, а в пределах чувствительных площадок элементов МПИ.
|
4Х |
![]()
|
Выб |
![]()
|
Рис. 9.2. Образование низкочастотной составляющей после выборки сигнала |
![]() В ИКС выборку сигнала могут выполнять растры, многоэлементные приемники, сканирующие системы, АЦП и др. При их использовании происходит усреднение сигнала, например потока излучения, проходящего через прозрачную ячейку растра или падающего на элемент МПИ, т. е. на выходе ячейки растра или элемента МПИ образуется сигнал, пропорциональный среднему по их площади значению входного сигнала.
В ИКС выборку сигнала могут выполнять растры, многоэлементные приемники, сканирующие системы, АЦП и др. При их использовании происходит усреднение сигнала, например потока излучения, проходящего через прозрачную ячейку растра или падающего на элемент МПИ, т. е. на выходе ячейки растра или элемента МПИ образуется сигнал, пропорциональный среднему по их площади значению входного сигнала.
Обычно принимают, что пропускание ячейки растра или чувствительность элемента МПИ характеризуются средним по их площади значением этого параметра.
8*
Сигнал на выходе МПИ, осуществляющего пространственную выборку (рис. 9.1), можно представить в следующем общем виде:
(*> у) = [sBX (X, у) * g3 (X, у)] r(x, у)а^ (х, у),
Где sBX(x,.y) - функция, описывающая распределение облученности в плоскости чувствительного слоя МПИ; g3(x, y) - распределение чувствительности по площади элемента МПИ, обычно принимаемое постоянным; /*(х,>’) — функция, учитывающая размеры площади чувствительного слоя МПИ и закон распределения элементов по этой площа - ди; а^(х, у) - функция, описывающая двумерную пространственную выборку изображения элементами МПИ, периоды расположения которых равны Хэ и Уэ по осям х и у соответственно, т. е.
«£(*>0=-“гХXцf-“m>7T-n = ,у-лУ).
Э Э Э Э у т=-оо«=-ао
Спектр функции sBblx(x, у ) имеет вид
Где функции 5ВЫХ(-), G(-), R{-) и (•) - спектры (преобразования Фурье) функций ЯвыхО* Яэ(-), г(-) и <£ (•) соответственно.
Связанное с конечностью значений чисел пикселов т (по оси х) и п (по оси у) приближение вполне допустимо в практике расчетов при МПИ больших форматов, т. е. при достаточно больших тип.
Спектр функции (1^{х, у) имеет вид
= - угг i, 2>(/< -<*•/,Z Ёад-К,./, - пГ„),
Э э т=-оол=-оо т--оо и~-оо
Л,= Ух„/.г=ук-
Для прямоугольной формы чувствительных элементов с размерами а и Ъ по осям х и у соответственно спектр функции g3(x, j) описывается выражением
G3(fx, fy) = sine (afx, bfy),
А спектр функции г(х, у)
R(fx, fy) = mXjiY3smc{mX3fx, nY3fy),
Где sinc(z)=sin(nz)/nz.
Объединяя приведенные выражения, можно получить формулу для спектра сигнала, образующегося после выборки, т. е. на выходе МПИ:
|
Т п |
Таким образом, очевидно, что спектр сигнала после выборки представляет собой спектр исходного сигнала (изображения), повторяющийся через интервалы/х=УХэ и f у- 1/Гэ, причем для отдельных полос этого спектра распределения амплитуд гармоник соответствуют (при т, п » 1) распределениям амплитуд функции Сэ([х, /у), т. е.
Этс(а/х, Ь/у).
Если частота выборки достаточно велика, а полоса частот, занимаемая исходным аналоговым сигналом (полоса пространственных частот, занимаемая спектром двумерного изображения в плоскости МПИ), ограничена, то после выборки и реконструкции можно получить выходной аналоговый сигнал, подобный исходному.
Максимальной частотой (гармоникой) сигнала, передаваемого и реконструируемого без искажений, является частота Найквиста равная половине частоты выборки /ВЪ}6, т. е. = /выб /2. Если какая-либо гармоника спектра исходного сигнала превышает имеет место наложение спектров, т. е. в спектре дискретизированного сигнала появляются ложные низкочастотные составляющие, в результате искажается реконструируемый сигнал, т. е. изображение на выходе ИКС [50, 61, 142.]. При этом на экране системы отображения может возникнуть растровая структура, во избежание чего при решении задач распознавания или идентификации используют так называемое сжатие передаточной функции системы или частот [113].
![]() Из анализа формулы для 5ВЪГХ(/Х, /у) следует важный вывод: искажения сигнала при усредняющей выборке тем больше, чем больше размеры а и Ь, т. е. чем быстрее убыва-
Из анализа формулы для 5ВЪГХ(/Х, /у) следует важный вывод: искажения сигнала при усредняющей выборке тем больше, чем больше размеры а и Ь, т. е. чем быстрее убыва-
|
|
|
/ |
|
2/выб / |
|
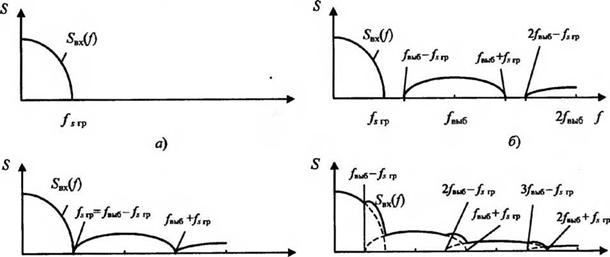
Рис. 9.3. Преобразования спектра сигнала 8ВХ{/) (а) при выборке с частотой/,ыб >2/^ (б), Увыб = = 2/; ф (в), Увыб < 2£ гр (г) |
Ют эшс-функции. С уменьшением а и Ъ 5ВЫХ(/Х,/У) приближается к спектру идеальной выборки. Если размеры а и Ь приближаются к периодам Хэ и Уэ, боковые полосы на частотах/^ = 1 /а,/у = 1/Ь и подавляются сильнее, что облегчает фильтрацию сигнала реконструирующим фильтром и улучшает восстанавливаемое изображение.
Изменения спектра сигнала при выборке показаны на рис. 9.3, где граничная частота спектра исходного сигнала 5ВЪ1Х(/) обозначена/ гр. При несоблюдении условия/вы6 > гр/2 епектр выходного сигнала не повторяет спектра исходного сигнала, т. е. имеют место искажения восстанавливаемого после выборки изображения. Чтобы избежать этих искажений или уменьшить их влияние, необходимо в качестве реконструирующего применять низкочастотный фильтр, отсекающий побочные (паразитные) гармоники сигнала. Важно отметить, что при^ =/выв /2< /хгр полностью устранить искажения восстановленного изображения не удается (см. на рис. 9.3,г перекрытие исходного спектра и первой побочной полосы с центральной частотойу^ыб).
Возникающее в результате наложения спектров искажение изображения называют редукцией пространственных частот, а также шумом пространственной дискретизации. Этот шум носит мультипликативный характер, поскольку зависит не только от параметров МПИ, но и от структуры исходного изображения. Способы уменьшения вредного влияния пространственной дискретизации могут быть различными. Самый простой из них — это ограничение пространственно-частотного спектра изображения до его пространственной выборки пространственным фильтром, которым служит апертурная диафрагма объектива или приемника с определенным законом распределения пропускания или чувствительности. Кроме того, изображение, подвергнутое выборке в отдельных равноотстоящих точках, можно занести в буферную память, а затем, умножив каждый отсчет на значение некоторой весовой функции, удвоить шаг между ними. Известны также способ разложения функции, описывающей изображение в ряд ортогональных функций Уолша и др. [113].
Поскольку искажение спектра изображения из-за наложения побочных спектров невозможно устранить в последующих звеньях электронного тракта, включая дисплей (систему отображения), остается только воспользоваться увеличением частоты выборки.
Рассмотрим механизм описания пространственной выборки, осуществляемой МПИ вдоль одной из ортогональных осей координат, без учета пространственного фазового сдвига или взаимного смещения изображения и МПИ, осуществляющего выборку, относительно исходного сигнала (изображения), который в общем случае может быть случайным. Первый минимум пространственно-частотной характеристики элемента МПИ приходится на частоту среза /хл= 1/аэ, где аэ - угол, стягиваемый элементом, имеющим линейный размер а. Обычно, для/'» а принимается аэ = а//', где /' - фокусное расстояние объектива, строящего изображение в плоскости МПИ.
Период пространственной выборки вдоль какого-либо размера поля обзора 2со0б3 равен (2сообз - аэУЛ'выб, где Л^б - число выборок. Соответственно, при 2сообз» аэ
Увыб * ^»ыб/^®об1
Если период расположения элементов МПИ равен Хъ, то частота Найквиста, ограничивающая пространственно-частотный спектр изображения, передаваемого без искажений, определяется как
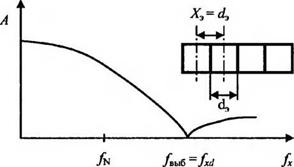
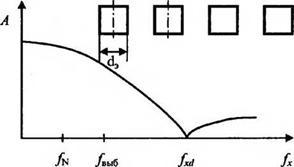 На рис. 9.4 показано изменение значений частоты Найквиста /к при изменении частоты выборкиУвЬ1б, определяемой периодом расположения Хэ элементов МПИ или растра, осуществляющего выборку. При одном и том же размере элемента с1э увеличение Х3 в два раза сопровождается соответственным уменьшением /к, что ведет к ограничению диапазона передаваемых без искажений частот в спектре исходного изображения также в два раза.
На рис. 9.4 показано изменение значений частоты Найквиста /к при изменении частоты выборкиУвЬ1б, определяемой периодом расположения Хэ элементов МПИ или растра, осуществляющего выборку. При одном и том же размере элемента с1э увеличение Х3 в два раза сопровождается соответственным уменьшением /к, что ведет к ограничению диапазона передаваемых без искажений частот в спектре исходного изображения также в два раза.
|
|
А б
Рис. 9.4. Изменение частоты Найквистапространственно-частотной характеристики МПИ
При 4Д3= 1 (а), с1/Хэ = 0,5 (б)
Частоту Найквиста, определяющую предельно разрешаемый без наложения спектров диапазон пространственных частот, можно увеличить, уменьшив период расположения чувствительных элементов МПИ, но не их размер. Иначе при этом из-за возможного наложения спектров ухудшится качество изображения, а следовательно, и вероятность его распознавания, классификации и т. д.
Нужно отметить, что ИКС «смотрящего» типа может обнаруживать сигналы от объектов, пространственные частоты которых превышают /ха, например сигналы от излучающих объектов с угловыми размерами, гораздо меньшими аэ, однако она не способна воспроизвести эти сигналы без искажений из-за последствий выборки - возникновения побочных гармоник и наложения (переналожения) частот в низкочастотной области спектра. Так, при калибровке ИКС с достаточно высокой частотой выборки по тест- объекту в виде миры, у которой пространственная частота превышает частоту Найквиста, изображение миры будет искажено и содержать меньшее число штрихов, чем тест - объект. При малой пространственной частоте выборки штрихи миры из-за сдвига спектра в область низких частот могут слиться в слабоконтрастную, достаточно однородную светящуюся структуру. Поэтому в системах «смотрящего» типа часто за граничную частоту принимают частоту Найквиста.
Помимо пространственной выборки входного сигнала многоэлементным приемником, аналого-цифровым преобразователем осуществляется и выборка аналогового сигнала во временной форме. Принципиально аналоговый сигнал можно преобразовать в цифровой на любой частоте, однако здесь также следует помнить о необходимости соблюдать условие Найквиста, в соответствии с которым сигнал, передаваемый без искажений, не должен иметь в своем спектре частот, больших/^ = 0,5/ВЬ1^.
Для ослабления описанного эффекта наложения пространственных частот, приводящего к уменьшению частоты Найквиста, можно использовать микросканирование (подробнее см. §9.3) либо предварительную пространственную фильтрацию в оптической системе, в которой изображение строится с использованием объектива с ОПФ, близкой по форме к прямоугольной, при верхней граничной частоте, равной частоте Найквиста. На практике идеальную прямоугольную характеристику получить невозможно из-за заметного спада ОПФ на высоких частотах, обусловленного потерей геометрооптического разрешения. Обычно размытием изображения реализуют приближение ОПФ к идеальному случаю. И если при этом потери энергии сигнала заметно меньше, чем при микросканировании, то разрешение гораздо хуже, так как теряются высокие пространственные частоты, характеризующие малоразмерные детали изображения и границы наблюдаемых объектов.
Предварительная пространственная фильтрация в оптической системе позволяет избежать эффекта наложения частот для объектов со сложной структурой, т. е. имеющих высокочастотные составляющие в пространственно-частотном спектре их изображений. Однако при этом приходится мириться с заметными потерями энергии сигнала.
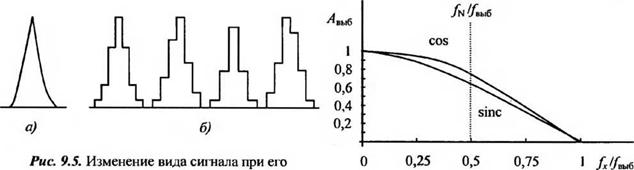
Системы с выборкой не инвариантны к сдвигу изображения относительно рисунка растра МПИ. Если изображение с периодической структурой в виде узких ярких полос попадает в промежутки между элементами чувствительной площадки МПИ, то сигнал, образующийся при выборке, будет минимальным. Напротив, если положения полос изображения и элементов МПИ точно совпадают, сигнал будет максимальным. В промежуточных вариантах, т. е. при изменении пространственной фазы (угла 9Л) между изображением и растром МПИ, амплитуда выходного сигнала будет иметь промежуточные значения. В качестве примера на рис. 9.5 показано изменение формы сигнала при его дискретизации, квантовании по уровню и осреднении внутри интервала выборки в случае, если пространственная фаза выборки изменяется. Очевидно, что передаточная функция процесса выборки будет зависеть от взаимного расположения изображения и МПИ. В общем случае (рис. 9.6) она имеет вид
Иногда некоторое среднее значение Лвыб([х) выбирают соответствующим 0* = 71/4. При этом с учетом того, что /к = 0,5 /шб,
4ь*(Л)=С08(л/х/2/вы6).
|
Пространственной выборке по оси х: а - вид исходного аналогового сигнала; Рис. 9.6. Усредненная передаточная функция Б - ступенчатые (квантованные) сигналы после процесса выборки, учитывающая взаимный сдвиг пространственных выборок с различной фазой изображения и растра МПИ |
В других случаях принимают (рис. 9.6)
В случае двумерного МПИ при оценке изменения спектра исходного сигнала из-за пространственной выборки необходимо учитывать ряд факторов: дискретность приемника по координате у; возможную неидентичность оптических передаточных функций по горизонтали и вертикали из-за астигматизма объектива или в редком на практике случае из-за использования анаморфотной оптической системы; возможное различие размеров чувствительных элементов и пикселов МПИ по горизонтали (по оси х) и по вертикали (по оси у); изменение пространственной фазы сигнала, снимаемого с МПИ, из-за смещения изображения по вертикали относительно растра МПИ; возможное различие в характере случайного (например, из-за вибрации) или задаваемого (при микросканировании) движения изображения МПИ похиу. Эти различия сказываются прежде всего на виде передаточных функций соответствующих звеньев ИКС и тем самым приводят к различным оценкам ряда критериев качества ИКС, например пространственного и температурно-частотного разрешения по горизонтали и по вертикали.
Механизм работы и формулы для расчета параметров и характеристик упомянутых звеньев ИКС идентичны для каждой из ортогональных координат. Тем не менее с учетом результатов ранее проведенного анализа одномерной выборки по оси х рассмотрим некоторые особенности процесса пространственной выборки, осуществляемой двумерным МПИ по координате у.
Частота выборки по у зависит от шага расположения чувствительных элементов, т. е. от периода выборки Уэ, и размера чувствительного элемента по вертикали Ь. Если Уэ и Ь взяты в угловой мере, т. е., например, приведены к фокусному расстоянию объектива/', то пространственная частота выборки (рад ’) определяется как
Где % - коэффициент перекрытия строк (заполнения) элементов МПИ по вертикали:
< 1 при Ъ < Уэ; Г[у = 1 при Ъ = Уэ; гу > 1 при Ъ > Уэ (отдельные столбцы элементов МПИ поочередно сдвинуты друг относительно друга вверх и вниз по оси у).
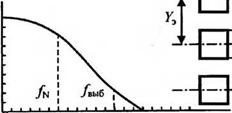
При различных ху, т. е. различных соотношениях между Ъ и Уэ, передаточная функция выборки (составляющая частотной характеристики устройства, осуществляющего выборку) меняет свой вид (рис. 9.7). При Ъ < Уэ и гу > 1 возможен случай, когда частота Найквиста будет больше граничной частоты (у ф, определяемой угловым размером Ъ//' чувствительного элемента:
При Уэ< Ь и > 1 избежать искажений спектра изображения при выборке из-за возникновения побочных низкочастотных составляющих возможно лишь при условии, что Уэ < Ь/2.
Таким образом, чтобы уменьшить искажения сигнала (изображения) из-за редукции частот при выборке, необходимо:
- ограничивать полосу частот сигнала,
- подбирать надлежащую частоту выборки,
- применять соответствующие конкретным параметрам сигнала и выборки реконструирующие фильтры.
Наибольшие принципиальные трудности вызывает первое из этих положений, поскольку спектр большинства реальных сигналов, поступающих на вход ИКС, содержит
|

|
0,5 Угд—1 /у Выб~2 Гу'/угр |
![]()
 •^выб 1
•^выб 1
0,4
|
А выб 1 0,8 0,6 0,4 0,2 |
![]() А)
А)
|
|
Рис. 9.7. Передаточные функции выборки при различных соотношениях между размером элемента Ь и периодом выборки К,: Ь > Уэ (а), Ь=Уэ(б)',Ь<Уэ(в).
Высокочастотные составляющие, соответствующие мелким деталям и краям отдельных фрагментов наблюдаемых объектов, а именно эти частоты (или малоразмерные структуры) чаще всего используются для выделения полезных сигналов на фоне помех и шумов при обнаружении, распознавании, классификации и определении координат объектов.
Эффективность геометрооптических методов распознавания и обработки изображений определяет не только число разрешаемых элементов изображения объекта, т. е. число пространственных выборок. Важным фактором, подлежащим обязательному учету, является фазовый пространственный сдвиг - смещение изображения или его отдельных разрешаемых фрагментов относительно растра МПИ, что особенно важно тогда, когда изображения отдельных фрагментов наблюдаемого объекта имеют различный фазовый сдвиг относительно МПИ или когда в процессе работы ИКС имеет место движение изображения относительно МПИ.
В то же время необходимо отметить способность зрительного аппарата человека интерпретировать не только идеальные, но и искаженные до определенной степени изображения. Это во многих случаях расширяет возможности ИКС и позволяет мириться с отклонениями от сформулированных условий оптимизации системы и отдельных её параметров и характеристик.
Практически во всех ИКС «смотрящего» типа именно пространственно-частотная характеристика (ПЧХ) приемника (его чувствительного элемента), но не ПЧХ оптической системы ограничивает спектр пропускаемых без искажений пространственных частот.