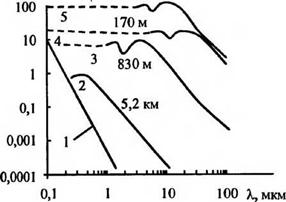
Инфракрасные системы «смотрящего» типа

РАССЕЯНИЕ

Поскольку аэрозольное рассеяние на частицах учитывает и поглощение излучения веществом, из которого эта частица состоит, правильнее говорить об аэрозольном ос­лаблении. Рассеяние на частицах характеризуется коэффициентом рассеяния ср - от­ношением рассеянного частицей излучения к излучению, падающему на частицу. По­глощение энергии частицей характеризуется коэффициентом поглощения стп - отноше­нием поглощенной частицей энергии к падающей на нее энергии.

Сумму <тр и а„ называют коэффициентом аэрозольного ослабления са:

Оа(Х) = ор(X) + оп(Х).

Иногда эти коэффициенты приводят к геометрическому сечению частицы, считая ее сферической с радиусом ас.

Наряду с аэрозольным ослаблением в атмосфере имеет место и молекулярное (рэлеев - ское) рассеяние, спектральный коэффициент ослабления которого определяется как

<Трэл(А.) = 0,83

3 2

Где Л'м - число молекул в 1 см А - площадь поперечного сечения молекулы, см ; X - длина волны излучения, см.

Некоторые значения арэл(А.) приведены в табл. 3.1. Очевидно, что в ИК-диапазоне спектра можно практически пренебречь молекулярным рассеянием, так как оно прак­тически не влияет на пропускание излучения. При работе в видимой и особенно в УФ - области оптического спектра его необходимо учитывать.

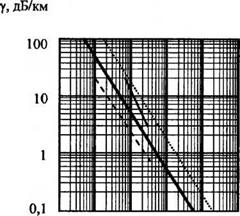
Теоретически рассчитанные и экспериментально полученные для среды, состоящей из сферических водяных частиц, зависимости показателей (коэффициентов) рассеяния аа от длины волны излучения X при различных состояниях атмосферы, характеризуе­мых метеорологической дальностью видимости, изменяющейся от 5,2 до 34 км [179], показаны на рис. 3.4.

В обычной форме закон Бугера для рассеивающих сред применим в тех случаях, когда:

- эффекты многократного рассеяния пренебрежимо малы;

- число частиц в рассеивающем объеме велико - гораздо больше единицы;

-каждая частица рассеивает излучение независимо от присутствия других.

Для крупнокапельных туманов (ас = 1...30 мкм) коэффициент ослабления сохраня­ется приблизительно постоянным для излучения с длинами волн от 0,35 до 3,70 мкм. Для средних туманов (ас = 0,1... 1,0 мкм) постоянство са наблюдается только в видимой области оптического спектра, а для мелкокапельных туманов са заметно изменяется во всем оптическом диапазоне. Для дождевых капель (ас = 0,1... 1,0 мм и более) в диапазо­не длин волн свыше 1 мкм оа«2и практически не зависит от длины волны.

Таким образом, для дымки и тумана рассеяние уменьшается с ростом длины волны излучения. Однако для сильных туманов и снега переход от видимого излучения к ИК не дает ощутимой выгоды.

А) б)

Рис. 3.4. Теоретические (а) и экспериментальные (б) зависимости показателя рассеяния от состояния атмосферы: 1 - рэлеевское рассеяние, 2 - чистый воздух, 3 - легкая дымка, 4 - дымка,

5 - легкий туман

Модель LOWTRAN предлагает эмпирическую формулу для учета рассеяния излу­чения на дождевых каплях

Оад *0,365i;fl0‘6

Где од - скорость выпадения осадков, мм-ч1 (табл. 3.2). В случае дождя общий коэффи­циент ослабления определяется только рассеянием на каплях и не зависит от длины волны излучения, т. е. тс = ехр (-СГад Г).

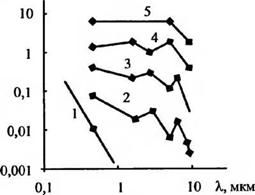
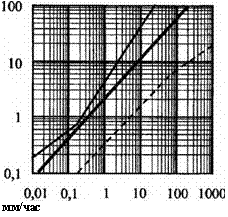
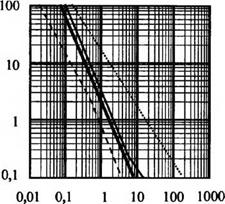
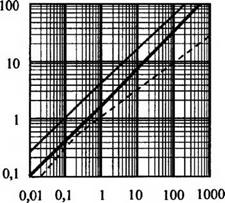
Помимо дымки, тумана, дождя и снега на работу ИКС могут заметно влиять и дру­гие аэрозоли, например пыледымовые образования. Некоторые данные об их учете при оценке рассеяния содержатся в [37, 151]. Примеры зависимостей коэффициентов ос­лабления излучения ух, вызванного влиянием рассеяния в ряде мутных (рассеивающих) сред на излучение с длиной волны X = 10,6 мкм, приведены на рис. 3.5 [151]. Аргумен­тами функций ух (дБ/км) являются метеорологическая дальность видимости лм (км), интенсивность дождя ид (мм/ч), интенсивность снегопада ис (мм/ч).

Данные о количественных характеристиках ослабления излучения атмосферными аэрозолями, приводимые в литературе, относятся большей частью к видимой области оптического спектра, что вызвано прежде всего трудностью измерения аэрозольных коэффициентов ослабления в ИК-диапазоне. Зависимость средних значений этих коэф­фициентов от высоты с точностью до 20% аппроксимируется выражением

Аа(ХД) = аа(Х,0)ехр(-раЯ),

Где ра - эмпирический коэффициент, выбираемый для различных метеорологических дальностей видимости 5М таким образом, что на высоте Н = 5 км коэффициент аа(А,,Я) оказывается постоянным (5-10 3 км-1 для А, = 0,5 мкм), на высотах 3...5 км уменьшается по сравнению со значением аа, измеренным у поверхности Земли, на один-два порядка Нужно отметить, что количественные характеристики аэрозольного и молекулярно­го рассеяния при горизонтальном распространении излучения отличаются от характе­ристик ослабления и рассеяния, наблюдаемых при распространении излучения по

У, дБ/км

У, дБ/км

0,01 0,1 1 10 100 1000

^м> КМ

У, дБ/км

Рис. 3.5. Зависимости коэффициентов ослабления излучения с X = 10,6 мкм от метеорологических параметров для чистого воздуха (а), тумана (б), дождь (в), снегопада (г), пыли (<)):

Среднее значение;----------- верхний предел;

--------- нижний предел,............ - >. = 55 мкм

Наклонным трассам. Достаточно строгих аналитических методов расчета для этого слу­чая пока не существует, поэтому необходимо использовать результаты эксперименталь­ных исследований (которых, к сожалению, проведено весьма мало) или приближенные способы учета наклонного хода излучения [24,25, 151].

При определении затухания излучения в рассеивающей среде обязательно учитыва­ются некоторые параметры излучателя и приемной оптической системы, влияющие на попадание в приемную систему не только ослабленного по закону Бугера прямого из­лучения, но и части рассеянного.

Для однократного рассеяния излучения от точечного источника в однородной и изо­тропной среде коэффициент та можно рассчитывать по формуле [24]

Тв = ехр(-Га)(1 + TJ)р),

Где Га = аа - / - оптическая толща рассеивающей среды; Dp - величина, зависящая от угловых апертур приемника и излучателя, а также от индикатрисы рассеяния частиц среды, но не от расстояния между излучателем и приемником. Очевидно, что при рас­пространении излучения через среду с Га в несколько единиц регистрируемый сигнал будет в несколько раз отличаться от сигнала, рассчитанного по закону Бугера. В таких случаях расчет следует вести по последней формуле, особенно для крупных частиц, когда Dp может достигать 0,5...0,7. При этом для Тл, равных нескольким единицам, вклад рассеянного излучения в общий сигнал может превышать вклад прямого ослаб­ленного потока в несколько раз. Формула однократного рассеяния в случае точечного источника справедлива при Тг< 10. При узких или коллимированных пучках границы применимости закона Бугера расширяются, но становится более заметным эффект мно­гократного рассеяния.

Помимо рассмотренных параметров среды, определяющих рассеяние, на практике используются и другие критерии, например метеорологическая дальность видимости sM - расстояние, на котором контраст между источником определенного типа (мирой) и окружающим его фоном снижается до порога контрастной чувствительности глаза, ха­рактеризует метеорологическое состояние среды (ее мутность):

. Ln(l/Ь "" «, '

Где аа - показатель рассеяния; ек - порог контрастной чувствительности приемника. Обычно для человеческого глаза принимают ек = 0,02. При этом для X = 0,55 мкм 3,91/аа о,55*

Международный код видимости и соответствующие sM значения аа приведены в табл. 3.3.

Если подставить аа из последнего выражения в формулу для коэффициента про­зрачности, то получим

Та 0,55 = exp(-aao, ssO = ехр(-3,91// 5М).

Иногда для расчета <ха в условиях, когда > 2 км и X < 3 мкм, пользуются формулой

АЛ=(ЗД»1/».Х>Л.55)_'. (3-3)

Где щ = 0,585 для плохих погодных условий (зм < 6 км), щ = 1,3 для средних метео­условий и щ = 1,6 для хороших.

Таблиц 3.3

Международный код видимости, метеорологическая дальность видимости 5М и показатель рассеяния аа0,55

С вводом критерия 5М условие применимости формул однократного рассеяния Тг < 10 выглядит как I < 2,5ям, т. е. при ям = 10 км (дымка) эти формулы справедливы для трасс длиной не более 25 км, а при лм = 200 м (туман) - для / < 500 м.

Для оценки рассеяния ультрафиолетового излучения в диапазоне 0,24...0,4 мкм при 5М= 4...40 км можно воспользоваться эмпирической формулой

0,538-X ( 0,08 V

Ух~ 0,0285М +и~0Д8; ’

Где ух = 4,340а - коэффициент затухания, км-1; X - длина волны излучения, мкм; 5М - ме­теорологическая дальность видимости, км.

Соотношения вида (3.2) и (3.3) позволяют рассчитать коэффициент прозрачности тах для любой X в пределах любого атмосферного окна. При этом поглощение вычисляют отдельно, независимо от рассеяния.

Общее ослабление излучения, т. е. коэффициент тс, после нахождения тп и та опреде­ляют по формуле (3.1).

На практике часто удобно пользоваться понятием «эффективный коэффициент пропускания среды (атмосферы) тсэф в пределах рабочего спектрального диапазона Х...Хг», который определяется как

3.2

X = —__________________

Сэф Х2 >

|Щ)т0(?фД>;)^

X,

Где L(X) - спектральная плотность яркости источника излучения; хс(Х) - спектральный коэффициент пропускания среды (атмосферы); т0(Х) - спектральный коэффициент про­пускания оптической системы ИКС; sv(X) - спектральная характеристика вольтовой чувствительности приемника излучения.

Если для визуализации ИК-изображения используется контраст яркостей объекта L0б и фона Ьф, на котором этот объект наблюдается, т. е. их разность, то в подынте­гральное выражение для хс эф вместо произведения L(X)xc(X) следует вводить разность Ьо5(Х)хс о6(Х) - Ьф(Х)хс ф(Х). Очевидно, при этом учитываются возможные различия в тс о6(Х) для объекта и тс ф(Х) для фона, связанные, например, с разными расстояниями от ИКС до этих излучателей. Вместо вольтовой чувствительности s„(A,) в формуле для тсэф можно использовать спектральную удельную обнаружительную способность приемника DX).

Понятие тс эф облегчает ряд расчетов и экспериментальных оценок параметров ИКС. Например, при определении эквивалентной шуму разности температур АТп (см. гл. 4) можно пользоваться достаточно простой формулой

А7; * Д7тсэф/р,

Где АТ - измеряемая разность температур объекта и фона, создающая отношение сиг­нал-шум, равное (J,.

Для прогнозирования работоспособности ИКС при изменяющихся атмосферных ус­ловиях важно учитывать динамику спектральной прозрачности атмосферы при суточ­ных и сезонных изменениях погоды в географических регионах, где работает ИКС. Не­которые статистические характеристики этого процесса для ряда районов Северного полушария Земли приведены в [37].