Инфракрасные системы «смотрящего» типа
ОБОБЩЕННАЯ СТРУКТУРНАЯ СХЕМА КОМПЬЮТЕРНОЙ МОДЕЛИ ОПТИКО-ЭЛЕКТРОННОЙ СИСТЕМЫ
Огромное разнообразие условий работы оптико-электронных систем (ОЭС), непрерывное расширение их элементной базы, совершенствование и усложнение алгоритмов обработки получаемой информации делают компьютерные методы параметрического и схемотехнического анализа и синтеза ОЭС незаменимыми при их проектировании, исследованиях и испытаниях. Моделирование позволяет существенно уменьшить объем дорогостоящего и не всегда достаточно представительного эксперимента, а в ряде случаев (например, при проектировании ИКС, работающих в условиях сложной фоноцелевой обстановки) и вообще отказаться от него. В полной мере это относится к созданию и исследованиям оптико-электронных систем визуализации (ОЭСВ), и в частности инфракрасных систем (ИКС). В то же время авторы ни в коей мере не хотят умалить роль натурных испытаний, значимость которых трудно переоценить.
К числу основных вопросов, на которые можно ответить с помощью моделирования ИКС, относятся:
- при каких значениях параметров и характеристик отдельных звеньев можно достичь поставленной перед ИКС цели;
- каково оптимальное сочетание этих параметров и характеристик;
- как будут влиять изменения условий работы ИКС (сценария, фоно-целевой обстановки и т. п.) на показатели качества системы;
- какие алгоритмы обработки информации, обрабатываемой ИКС, наиболее рациональны с точки зрения различных требований, предъявляемых к системе, в частности, для обеспечения заданных показателей качества.
Первые аналитические модели ИКС представляли собой развернутые, т. е. представленные в виде функции многих параметров системы, выражения для важнейших показателей (критериев) качества ИКС - эквивалентной шумам разности температур АТП и минимальной разрешаемой разности температур А7р. Помимо этого, к аналити-
11 Инфракрасные системы «смотрящего» типа -
Ческим моделям довольно часто относят вероятностные модели задач, решаемых с помощью ОЭС, например, по обнаружению, распознаванию, идентификации различных объектов.
Одной из оценок качества той или иной модели ОЭС является степень ее адекватности (или просто адекватность) реальным условиям работы системы и значениям ее конструктивных параметров и характеристик. Это определяется многими факторами, и в первую очередь адекватностью отдельных субмоделей, т. е. полнотой и достоверностью описания полезных сигналов, фонов, помех и шумов, имеющих место в конкретных условиях работы ОЭСВ, а также допусками на разброс отдельных параметров и характеристик элементов и узлов ОЭС и допустимыми отклонениями показателей качества системы от их номинальных (задаваемых) значений.
Степень адекватности достаточно обобщенной компьютерной модели ОЭС, построенной по жесткой схеме (алгоритму), зависит от ряда факторов, к числу которых на практике чаще других относятся:
- изменение условий работы системы (сценария работы ОЭС, окружающих условий и т. д.);
- замена одного метода просмотра и анализа пространства объектов (поля обзора) другим, например оптико-механического сканирования просмотром поля с помощью двумерного МПИ;
- изменение алгоритмов (способов) фильтрации полезного сигнала на фоне помех, обнаружения, распознавания, слежения и т. п.;
- замены в элементной базе системы, например, отдельных узлов и элементов новыми, более совершенными, но и более сложными или, напротив, менее сложными, но более дешевыми.
Сюда же можно отнести и такой субъективный фактор, как возможная недостаточная опытность пользователя моделью, поскольку работа с большинством современных компьютерных моделей ОЭС происходит в диалоговом дружественном режиме.
С адекватностью компьютерной модели как показателем ее качества или требованием к ней тесно связаны ее универсальность, т. е. возможность использования при решении достаточно широкого круга практических задач, а также технико-экономическая эффективность, определяющая по тому или иному критерию выигрыш данного вида моделирования по сравнению, например, с физическими или натурными испытаниями макетных или опытных образцов ОЭС.
Структура типовой ОЭС и ее обобщенной компьютерной модели, а также структурные схемы ряда моделей конкретных видов ОЭС неоднократно рассматривались в литературе [38, 48, 116, 142, 149, 159, 168, 188, 198, 226, 227, 239, 240, 256, 262, 267 и др.].
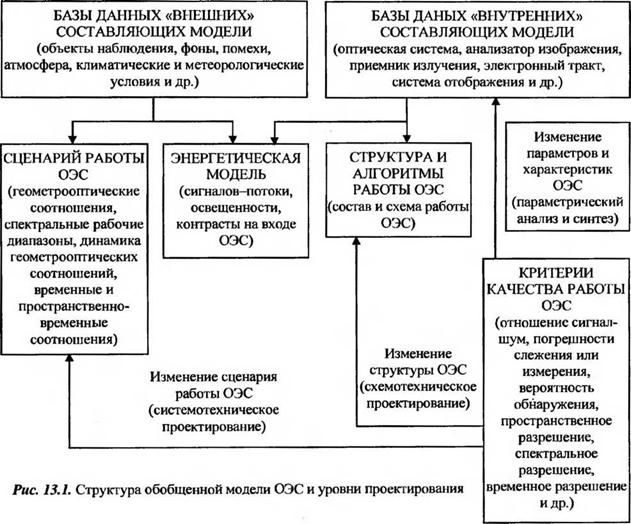
За достаточно обобщенную модель ОЭС можно принять структуру, представленную на рис. 13.1. Компьютерную оболочку этой модели определяют ее главные компоненты - файлы (субмодели) «Сценарий работы ОЭС», «Энергетическая модель», «Структура и алгоритмы работы ОЭС», «Критерии качества работы ОЭС», включая базы данных, разделенные на две большие группы:
- сценарий и энергетическая модель;
- отдельные узлы и элементы (их схемы, параметры и характеристики), а также типовые алгоритмы обработки информации, используемые в современных ОЭС.
На том же рис. 13.1 указаны некоторые возможные использования компьютерной модели ОЭС на различных этапах проектирования системы [48]. В принципе, отдельные и даже все базы данных могут отсутствовать в модели, однако в этих случаях работа пользователя с моделью заметно усложняется.
|
|
Феноменологические субмодели и соответствующие им базы данных описывают сигналы, поступающие на вход ОЭС от наблюдаемых или контролируемых объектов (целей), фонов и помех, а также преобразования этих сигналов в среде их распространения от источника сигнала до входа ОЭС. Эти субмодели и базы («Сценарий работы ОЭС», «Энергетическая модель», «Атмосфера», «Фоны» и др.), пожалуй, наиболее сложные, поскольку чрезвычайно большое число возможных сценариев работы ОЭС, достаточно строгое описание физических процессов возникновения и распространения оптических сигналов, многомерность оптических сигналов и ряд других факторов
И*
Весьма затрудняют их адекватное математическое воспроизведение и могут заметно усложнять компьютерную модель.
Одним из вариантов модели исследуемого и используемого сценария может быть геометрооптическая схема, представляющая совокупность излучателей (объекта, помех, фонов, среды распространения оптического сигнала), имеющих место в конкретной ситуации, а также их взаимное расположение (дальность, высоты, углы). Другим вариантом модели может быть синтезированное или получаемое каким-либо другим путем изображение сцены (углового поля ОЭС).
В качестве выбираемых или задаваемых параметров и характеристик излучателей, входящих в модель, можно использовать температуры, излучательные и отражательные способности, геометрические размеры излучающих или отражающих поверхностей и их ориентацию относительно ОЭС и относительно друг друга, спектральные характеристики и др. Сигнатуры сигналов от объектов, фонов и помех часто описываются хорошо известными зависимостями типа закона Планка, однако сложный, а порой и непредсказуемый характер собственного излучения, отражательной способности и процессов теплообмена в многофакторном пространстве объектов очень затрудняет их адекватное математическое отображение.
На первых этапах создания модели (выбор и анализ рабочего сценария) приходится выбирать и учитывать размер углового поля или площади, просматриваемых ОЭС, динамику платформы-носителя системы, а также временные изменения условий ее эксплуатации. Последнее включает учет времени года и суток, возможные изменения климатических и метеоусловий, например уровня солнечной освещенности, скорости ветра и других подобных факторов.
Синтез необходимого изображения может начинаться с выбора одного из изображений (сцены), содержащихся в базе данных. Для геометрической коррекции базового изображения используют различные процедуры, которые позволяют изменять взаимное геометрическое положение ОЭС, объекта, фонов и помех, например положение оптической оси ОЭС и линии визирования относительно объекта или фона, на котором наблюдается объект. Кроме того, можно изменять яркость отдельных участков сцены, например объектов или помех, в соответствии с различиями в их коэффициентах отражения и излучения, вводить в сцену дополнительные объекты или помехи, учитывать переход к новому, отличному от исходного (для базового изображения) спектральному диапазону и т. д.
В начале моделирования задают географические, климатические и другие условия, в которых работает ОЭС. Географическая база данных обычно содержит сведения о координатах ОЭС и наблюдаемого объекта (широта, долгота, высота), о типе территории, на которой работает ОЭС, и топографических признаках этой территории (тип местности, растительность, водоемы и т. п.). Здесь же следует учитывать погодные условия, которые определяют наличие фоновых и помеховых излучателей типа атмосферы и облачности, а также условия прохождения сигналов на трассах от излучателей (объектов, фонов, помех) до ОЭС. Во многих случаях это необходимо для оценки энергетических характеристик, например излучательной способности, не только фонов и помех, но и наблюдаемых или контролируемых объектов.
После этого можно учесть различия в параметрах и характеристиках среды распространения излучения для базового и синтезируемого изображений, которые обусловлены изменениями спектральных диапазонов работы, протяженности трасс. Для учета влияния среды — атмосферы часто можно воспользоваться моделями стандартной атмосферы типа моделей ГИПО, LOWTRAN, MODTRAN и др. [25, 151, 178, 196 и др.].
Нужно сказать, что даже эти хорошо освоенные и широко используемые субмодели, описывающие возникновение и распространение оптических сигналов в атмосфере и основанные на сочетании теоретических и эмпирических зависимостей, хотя и занимают большой объем памяти в базах данных компьютерных моделей, не всегда достаточно адекватно отражают возможные ситуации, возникающие при работе ОЭС.
Следует отметить, что реализация идеальной модели, учитывающей все энергетические, спектральные, геометрооптические, временные параметры и характеристики трехмерного пространства (просматриваемой сцены) с точным выполнением всех физических законов, требует практически отсутствующих времени моделирования и объема памяти компьютера. Поэтому часто имеет смысл перейти к упрощенным субмоделям «Сценарий работы ОЭС» и «Энергетическая модель», в основном, сохраняющим адекватность, но позволяющим разрешить указанную проблему. Учитывая весьма большое многообразие возможных ситуаций (сцен, сценариев, фоно-целевых обстановок), в которых могут работать ОЭС, целесообразно и допустимо для решения основных задач с помощью моделирования ОЭС, например, для параметрического анализа системы совмещать расчет параметров и характеристик излучателей и сред распространения оптических сигналов на основе достаточно строгих физических закономерностей с использованием баз данных, полученных эмпирическим путем.
Несколько более простыми представляются параметрические субмодели, описывающие отдельные звенья ОЭС и процесс обработки в них сигналов («Оптическая система», «Приемник излучения», «Электронный тракт», «Система отображения» и др.). При их построении необходимо принимать во внимание большой объем и непрерывное обновление баз данных, в которых сосредоточены сведения о параметрах и характеристиках отдельных звеньев ОЭС, а также трудность учета возможных разбросов значений этих параметров и характеристик.
Передаточные функции (частотные характеристики) отдельных звеньев и всей ОЭС, входящие в выражения для оценки важнейших параметров качества системы, например, в формулу для Д7р, характеризующую качество работы ИКС (см. гл. 4), обычно определяют в предположении, что все звенья системы работают в линейном режиме, а общую передаточную функцию ОЭС G03c находят как произведение передаточных функций ее отдельных звеньев. Таким образом,
Go3c(fx)=G0MdGMGmGMx)Grn(f^GOCH(fxl (13-1)
Где Gom(fx), Gnil(fx), G3(fx), GJfx Gm(fx), G0CH(fx) - передаточные функции (частотные характеристики) оптической системы, приемника излучения, электронного тракта, системы отображения, глаза наблюдателя, движения основания соответственно; fx - пространственная частота, которая может быть одномерной, характеризующей одномер
Ную структуру или меру повторяемости вдоль одной координаты, а также двумерной (£, /у) или векторной Ор) величиной. Эти функции являются Фурье-преобразованиями соответствующих импульсных реакций перечисленных звеньев ИКС.
При моделировании ИКС «смотрящего» типа необходимо учитывать особенности обработки сигналов (изображений в аналоговой и цифровой форме), отмеченные выше (см. § 9.1) и состоящие в размытии изображения до выборки, выборке отдельных значений сигнала, размытии дискретизированного после выборки сигнала, т. е. его реконструкции к аналоговой форме. Первый из этих процессов (размытие изображения до выборки) обычно описывается гауссовской функцией (импульсной реакцией) и соответствующей передаточной функцией, второй - совокупностью отдельных значений дискретизированной функции (сотЬ-функцией), третий - типом звеньев, используемых при реконструкции изображения. При использовании для размытия реконструируемого изображения системы отображения на базе катодно-лучевых трубок импульсная реакция этой системы принимается гауссовской, а системы отображения на базе дискретных электролюминесцентных или светодиодных панелей - прямоугольной. (Более подробно передаточные функции отдельных звеньев ИКС будут рассмотрены в § 13.4.)
Как уже неоднократно отмечалось, выборка изображения, осуществляемая в ИКС «смотрящего» типа, - нелинейная операция, что необходимо учитывать при определении передаточных функций таких систем. Для линеаризации передаточной функции (функции передачи модуляции) можно использовать ее «сжатие» в области частот, близких к частоте Найквиста (см. гл. 9). Такой путь избран, например, в моделях ПЛЯ92 и ЫУТЬегт (см. § 13.2, а также [113, 265, 266]). К другим источникам нелинейностей, которые обычно приходится учитывать при моделировании ИКС, относятся нелинейность систем отображения, а также зрительного аппарата человека-наблюдателя.
Отдельным блоком структурной схемы обобщенной компьютерной модели ОЭС является субмодель «Критерии качества ОЭС». Учитывая многофункциональный характер многих ОЭС, например приборов, служащих для поиска, обнаружения, распознавания, слежения и определения координат объектов, часто приходится рассчитывать значение не только какого-либо одного критерия качества, например, отношения сигнал - шум на выходе ОЭС, но и целую совокупность их (выходных параметров), например, характеристики обнаружения, погрешности слежения и др.
Показателями (критериями) качества ИКС визуализации чаще всего считают минимальную разрешаемую разность температур АТр и эквивалентную шуму минимальную обнаруживаемую разность температур АТП, хотя их использование подразумевает ряд условий и ограничений: пространственное и энергетическое разрешение оценивается по тест-объекту определенной конфигурации, время наблюдения не ограничено, зрительный аппарат наблюдателя - идеальное интегрирующее звено, наблюдатель знает о расположении объекта и др. [34, 144]. При этом часто не учитывается реальный характер шумов, имеющих место в системе, а принимается априорно гипотеза о нормальном распределении спектра шума. Предполагается, что все звенья ИКС, включая глаз наблюдателя, работают в линейном режиме.
В модели ИКС третьего поколения нужно учитывать все эти факторы, действующие для конкретной системы в пределах полосы пропускания частот, а не в пределах некоторой стандартной полосы пропускания, что имело место при определении эквивалентной шумам разности температур для ИКС первых поколений. В последнее время в связи с тенденциями использовать двумерные МПИ, т. е. переходить к «смотрящему» режиму работы ИКС, когда особое значение приобретают процессы пространственной и пространственно-временной выборки оптических сигналов, возник ряд особенностей моделирования таких систем, связанных, например, с аналого-цифровым преобразованием сигналов, их квантованием и реконструкцией, с ограничениями спектров передаваемых сигналов частотой Найквиста, с корреляцией сигналов, получаемых с разных элементов МПИ, с увеличением влияния неоднородностей параметров отдельных элементов приемника (геометрического шума) и др. Предпосылки для их учета рассматриваются в публикациях, посвященных ОЭС [83, 111, 112, 142, 199, 265], а также в этой книге.
Еще одна принципиальная особенность модели ИКС третьего поколения связана с определением или использованием пространственного разрешения не по одной координате (вдоль критического размера объекта), а по двум ортогональным. Как уже отмечалось в гл. 4, в настоящее время АТр предлагается определять для пространственной частоты, вычисляемой как квадратный корень из произведения пространственных частот, соответствующих АТр, измеренных для горизонтального и вертикального направлений.
Если в моделях ИКС первого и второго поколений качество системы ограничивалось шумами отдельных звеньев, то уже сейчас отмечается, что в ряде современных ИКС это качество лимитируется недостаточным контрастом изображения на экране выходного дисплея, что приводит к необходимости работы человека-оператора (наблюдателя) в затемненных условиях, т. е. пороговое отношение сигнал-помеха не остается постоянным, а изменяется в зависимости от условий работы наблюдателя. Наконец, предлагается учитывать пространственный предел интегрирования изображения глазом (4 мрд), в то время как в известных ранних моделях предполагалось, что интегрирование идет по всему изображению объекта (цели). Последнее позволит уточнить определяемое с помощью модели пространственно-температурное разрешение ИКС АТр в области низких пространственных частот.