Инфракрасные системы «смотрящего» типа
ФЛУКТУАЦИИ ПРОЗРАЧНОСТИ АТМОСФЕРЫ И ИХ ВЛИЯНИЕ НА РАБОТУ ИКС
При распространении излучения в атмосфере наблюдаются не только его поглощение и рассеяние, но и флуктуации его параметров (интенсивности, фазы, угла прихода и др.), обусловленные турбулентными явлениями - колебаниями температуры, влажности, плотности воздуха, а следовательно, и его показателя преломления п. В первом приближении зависимость показателя преломления воздуха от давления Р и температуры Т имеет вид
П = 7,9-1(Т2Р/Т+ 1,
Где Р измеряется в атмосферах, а Г - в градусах Кельвина.
В результате турбулентных движений в атмосфере создаются оптические неоднородности, размеры которых колеблются от нескольких миллиметров до сотен и более метров. Флуктуации амплитуды и фазы волны в оптическом пучке приводят к изменению его структуры, расширению, флуктуациям направления пучка и интенсивности сигнала. Чем ближе зона турбулентности к ИКС, тем больше ее влияние на качество изображения, создаваемого системой.
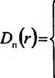 Для анализа влияния флуктуационных процессов на распространение излучения в атмосфере удобно воспользоваться структурными функциями, описывающими пространственную дисперсию случайного распределения п. Вид этих функций зависит от характера (модели) турбулентности. Для локально изотропной и однородной турбулентности (модель Колмогорова-Обухова) они имеют вид
Для анализа влияния флуктуационных процессов на распространение излучения в атмосфере удобно воспользоваться структурными функциями, описывающими пространственную дисперсию случайного распределения п. Вид этих функций зависит от характера (модели) турбулентности. Для локально изотропной и однородной турбулентности (модель Колмогорова-Обухова) они имеют вид
С11Г(г/1Л при 0 < г < /0;
C„V/3 при l0<r<L0;
Const при r>L0,
Где г - расстояние между двумя точками случайного поля п; /0 и L0 - внутренний и внешний масштабы турбулентности (размеры наименьших и наибольших неоднородностей атмосферы); Сп2 - структурная постоянная турбулентности показателя преломления, характеризующая влияние неоднородностей атмосферы на распространение оптического излучения.
Величины /0 и Lo зависят от высоты над землей. В приземном слое /0 = 1...2 мм и Lq = 5... 10 мм, а на высоте Нони определяются как /0 = (10-9Н),/3 и Ь0 = (4Н)т, если /0, Lo и Я выражены в метрах.
Значение Сп2 зависит от времени суток, метеорологических условий, высоты над землей. Например, в солнечный день, когда градиеАты температуры велики, значения Сгп на порядок больше, чел в облачный день. Чем более пересеченной является трасса, по которой распространяется излучение, тем больше эти градиенты и, следовательно, Сп2. Зависимость Сп2 от высоты Н в метрах можно определить как
Где С20 - значение С2 на высоте 1 м над поверхностью земли. В одной из моделей, используемых для расчета Сп2п, атмосфера разбивается на несколько слоев, внутри каждого из которых С2 принимается постоянной, т. е. ее значения берутся равными: 8,4-10"15 при Яот 0 до 18,5 м; 2,87-10“12/Я2от 18,5 до 110 м; 8,4-10“15 от 110 до 1500 м; 8,87-10~7/Я2 от 1500 до 7200 м; 2,0-10~1б/Я'Лм-2/3 от 7200 до 20000 м.
Другая модель (Хюфнагеля-Волли) предусматривает расчет Сп2 по формуле
Cl (я)= 5,94■ 10-53(ин /27)Я1Оехр(-Я/1000)+
+ 2,7 • 10~16 ехр (- Я /1500) + Л ехр (- Я /100),
Где высота Я измеряется в метрах, средняя скорость ветра vH на высоте Я - в метрах в секунду, А = 1,7-10-14 м“2/3. В свою очередь скорость ветра vH может быть рассчитана как
VH = 5 + 30 exp {-[(Я - 9400) /4800]2}
Нужно указать, что влияние турбулентности сказывается лишь в тех случаях, когда время наблюдения превышает так называемую атмосферную постоянную времени, которая равна
|
Т = 0,058 Атм > |
![]() 3/5
3/5
Sec zlCl(H)v5,3(H)dH
Н и
Где 2 - угол возвышения линии визирования; X - длина волны излучения.
В последние годы на основе экспериментальных определений структурной постоянной С1 при различных метеорологических условиях было предложено несколько моделей для вычислений значений С2п по известной температуре (/С), относительной влажности Оо™ %) и скорости ветра (ин, м/с). Хорошее совпадение с экспериментом дала следующая регрессионная модель [180]:
Сгп = а, Ж + ЬХ1 + с, оотн + сга1и + с3а^ + с1р + (12ьг + еГ3и3 + е,, где С1 измерена в м_2/3; аи Ьь си..., е, - коэффициенты регрессии, равные
А1 = 3,8-1014; Ь = 2,0-10‘15; = 2,8-10“15;
С2 = 2,9-1017; с3 =-1Д-10"19; </, = -2,5-10 15; а2 = 1,2-1015; dъ = -8,5-10"17; ^ =-5,3-10“13,
W - весовой коэффициент, учитывающий время наблюдений (за время начала отсчета взято время восхода Солнца, а его заход принят происходящим через 11 часов). Значения коэффициентов IV зависят от времени суток. Для различных интервалов времени, отсчитываемых от момента восхода Солнца (0 часов по выбранной шкале времени), они равны:
|
Интервал, ч |
Значение W |
Интервал, ч |
Значение W |
|
0,011 |
5...6 |
1,0 |
|
|
-3...-2 |
0,07 |
6...7 |
0,90 |
|
-2...-1 |
0,08 |
7...8 |
0,80 |
|
-1...0 |
0,06 |
8...9 |
0,59 |
|
(восход Солнца); |
|||
|
0...1 |
0,05 |
9...10 |
0,32 |
|
1...2 |
0,1 |
10...11 |
0,22 |
|
2...3 |
0,51 |
11...12 |
0,10 |
|
3...4 |
0,75 |
12...13 |
0,08 |
|
4...5 |
0,95 |
13 |
0,13 |
Еще лучшее совпадение с экспериментом дала модель следующего вида:
Сгп = APw+BJ+с1рати + с2р<4 + с, р<4 +
+ Ар + А2р + Л3р + Vc + + Ргра1 +
Где Сгп измеряется в м_2/3, Т - абсолютная температура в Кельвинах; W, аоти, v - в тех
Же единицах, что и в предыдущей формуле; Ар, Вip, Сip, .... Gp - коэффициенты регрессии, равные
Ajр= 5,9-10-15; В1р= 1,6-Ю“15; С1р = -3,7-1015; С2р = 6,7-КГ17;
С3р - -3,9-10Г19; Dlp =-3,7- 1<Г15; D2p = 1,3-Ю“15; D3p = -8,2-10'17;
Ер = 2,8-Ю-14; Fp = -1,8-1(Г14; F2p = 1,4-1014; Gp = -3,9-10-в,
Sc - солнечная постоянная, кал-см ^мин1; - общая площадь поперечного сечения
2 3
Рассеивающих частиц, содержащихся в одном кубическом метре среды, см /м.
Мерой мерцания — флуктуаций интенсивности приходящего оптического сигнала - служит дисперсия флуктуаций логарифма силы излучения источника
Когда длина трассы много больше внешнего масштаба турбулентности, распределение плотности вероятности Ps интенсивности сигнала подчиняется логнормальному закону. Для однородной турбулентности атмосферы на трассе длиной I при слабых флуктуациях (стм « 1) в случае приема излучения точечным приемником (системой с малым входным зрачком)
|
|
(3.5)
Где кх =2п1Х. При этом должно соблюдаться условие I < /02 / X. При увеличении / значение ом не возрастает бесконечно, а стремится к некоторому пределу.
При увеличении диаметра входного зрачка D мерцание уменьшается не беспредельно. Реально таким путем удается снизить стм лишь до 30% его значения, найденного по формуле (3.5).
Мерцание имеет низкочастотный временной спектр, максимум которого приходится на частоту fm^-0,32vL/ - JtJ, v± — скорость ветра в направлении, перпендикулярном направлению распространения излучения.
С увеличением зенитного расстояния z наблюдаемого внеатмосферного источника амплитуда мерцания возрастает по закону sec z, так как увеличивается масса воздуха. Частота мерцаний в этом случае уменьшается с ростом г. Так, у горизонта частота обычно не превышает 5... 10 Гц, а вблизи зенита она достигает иногда 103 Гц.
Изменения оптической длины хода лучей вследствие турбулентности приводят к флуктуациям фазы вдоль и поперек пучка. Поперечные флуктуации нарушают пространственную когерентность на волновом фронте, искривляют и изгибают пучок, вызывают дрожание изображения. Флуктуации вдоль пучка уменьшают его временную когерентность.
![]() Выражение для структурной функции фазы ф имеет вид [24]
Выражение для структурной функции фазы ф имеет вид [24]
|
|
2,УЛ‘/Сп г при
1,46k2JCl rsn при 10<г<л/aZ
Дисперсия угла прихода излучения для системы с входным зрачком И определяется как
2 1,46 D 1/3 Сп2 / при 10<D<-J}T,
Op =< __
1 2,9 D-mC2nl при /0 >£>>лД7.
Среднее квадратическое отклонение угла прихода на приземных трассах (дрожание изображения) составляет единицы и десятки секунд. Как и мерцание, дрожание возрастает по закону sec z, т. е. увеличивается с ростом зенитного расстояния z при наблюдении звезд или других внеатмосферных излучателей.
Спектральная плотность мощности (распределение дисперсии по частотам дрожания) имеет низкочастотный характер (практически определяется диапазоном ОД... 100 Гц). Максимум этого спектра наблюдается при частоте/щ,. = 0,22i)±/D.
Дисперсия дрожания медленно убывает (по закону степени -1/3) с ростом времени осреднения получаемых в процессе измерения результатов. Например, для погрешности измерения смещения пучка в доли миллиметра необходимое время осреднения иногда составляет несколько десятков секунд.