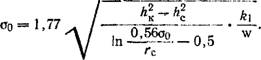ГИДРО­ГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ

Учет неравномерности инфильтрации

Неравномерность инфильтрации наиболее существенно сказы­вается при работе скважин вертикального дренажа и сравнительно близком положении уровня грунтовых вод (2,5—3 м). В этом слу­чае с приближением к скважине интенсивность инфильтрации (в среднем за вегетационный период) будет возрастать за счет меньшей разгрузки грунтовых вод на испарение и транспи - рацию.

В первом приближении при небольших понижениях можно при­нимать линейную зависимость интенсивности испарения от глубины уровня грунтовых вод вида w_ = wj (1 — z/zq) , а суммарную ин­тенсивность площадного питания w получать, вычитая величину w - из интенсивности питания при поливах wn. Решение задачи для стационарного планово-радиального потока при сеточном площад­ном дренаже и задании такой изменчивости площадного питания позволяет получить расчетное значение wpaC4, задавая которое можно использовать приведенные выше зависимости при равномер­ной инфильтрации. Значение wpaC4 представляется следующим вы­ражением:

Л

WpaC4~ WCp + (Wn — Wcp), (3.65)

Rtc

Где Г\ — радиус зоны вблизи скважины с глубиной до уровня грун­товых вод, превышающей zq, a wcp — средняя величина интенсив­
ности инфильтрации в зоне от г\ до гк, определяемая по выраже­ниям

2Awr 1 Wcp:=----------------------------- з—з-- <3-66>

BW (/к — ri) f(rK)- In ^--0,5 ГК~Ґ1

Г с

— г и. / Bw к к \ ~f~'

Kn

Wn+ Wq l)

Aw — —----------- —---------------- 4 (3.66a)

1 _j. 0 n

Гфп

А значение / (r„) находится по табл. 36.

При оценке работы горизонтального дренажа в условиях про­мывок или интенсивных поливов напускном возникает задача учета неравномерности скорости просачивания на междудреньи, которая во многих случаях оказывается весьма значительной (см. гл. 2, § 2). Например, наблюдения, проведенные на участке опытных промывок в совхозе № 4 Голодной степи, показали, что на рас­стояниях от 4 до 27,5 м от временной дрены скорость просачивания менялась от 67—93 до 5—7 мм/сут, т. е. более чем на порядок. Теоретическое описание такой неравномерности оказывается доста­точно сложным в силу необходимости учета таких факторов, как планировка поля, образование кольматационной пленки на по­верхности земли, плановая неоднородность строения зоны аэрации, влияющих на формирование скорости просачивания. В связи с этим представляется целесообразным рассматривать в качестве одного из перспективных методов реализации рассматриваемой задачи об­щее решение уравнения планово-плоского фильтрационного потока к линейному дренажу с учетом произвольного распределения (по профилю) скорости инфильтрации с поверхности земли с после­дующим учетом установленного в натуре характера неравномерно­сти скорости просачивания для конкретных природно-хозяйствен - ных условий.

Общее решение уравнения одномерного потока при произвольном распре­делении по профилю скорости просачивания (интенсивности инфильтрации) vnp имеет вид

Я + + + 0, Wx=^onpdxdx. (3.67)

О о

Для полуоткрытого ограниченного потока с граничным условием III рода на дрене (при х=0), найдя произвольное интегрирование С, и С2, запишем ре­шение такой задачи в виде

Fi1^ (3.68)

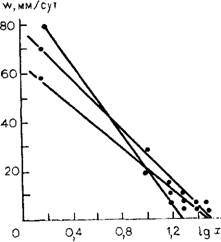
Где Wb определяется как Wx при х=0,Ы Практическая реализация этой задачи требует задания вида зависимости иПр(*). По некоторым данным (рис. 50) такая зави­симость имеет логарифмический характер (упр«А —В In*).

Установив экспериментальным путем характер распределения в зоне влияния дрены, целесообразно затем найти расчет­ное среднее значение интенсивности инфиль­трации (Шрасч) с тем, чтобы использовать для расчетов дренажа общую методику, хорошо разработанную для случая o>=const (см. § 3). В качестве примера приведем Зависимость ДЛЯ Определения Шрасч при логарифмическом характере изменения

Япр(*)

Wpac4 — А

— 1

(3.69)