ГИДРО­ГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ

Схемы промачивания зоны аэрации

Процесс промачивания зоны аэрации находится в зависимости от гидрофизических характеристик пород и условий поступления воды на дневную поверхность. Теория этого процесса достаточно подробно разработана Дж. Филипом [12] путем анализа решений уравнения (2.32). Им было доказано, что для большинства случаев инфильтрации влаги в сухие породы при затопленной поверхности скорость инфильтрации определяется простым соотношением

+ (2.39)

Где 5 — сорбционность; А—-некоторый параметр, который при t-> оо стремится к коэффициенту фильтрации k0. Соответственно объем впитывания V определяется по формуле

F=SVH-A/. (2.40)

Вначале, когда преобладают процессы впитывания за счет дейст­вия капиллярных и сорбционных сил, вторым членом в формуле (2.40) можно пренебречь. Для этого периода характерно соотно­шение

Vt=±V.

Это соотношение справедливо для всего периода времени при впи­тывании в горизонтальном направлении. Выражение для сорбцион- ности S и консганты А определяется зависимостями k (9) и Из решения уравнения (2.34) при п = 1 следует

-V4

Анализ решения Дж. Филипа [12] приводит к очень близкому по форме выражению

S = (2.41)

Как видно, несмотря на некоторые различия в числовых коэф­фициентах, физический смысл константы S во всех случаях оди­наков.

Для анализа процесса инфильтрации используется также гид­равлическая модель [12]. В соответствии с этой моделью движение влаги происходит при полном насыщении под действием капилляр­ных и гравитационных сил. Интенсивность промачивания опреде­ляется следующей формулой:

О=г*0 Щ+^tL, (2.42)

Где I — глубина промачивания; Н° — высота слоя воды над поверх­ностью земли. Скорость продвижения фронта и определяется в за­висимости от дефицита влажности [л, = 6ТО—0е (0е— начальная влажность)

V dt.„. ы==1Г^-ЗГ (2-43)

Совместное решение уравнений (2.42) и (2.43) относительно вре­мени продвижения фронта на глубину имеет вид [12]

(//к-яо)іп(І+77-^ж);

Дж. Филипом [12] теоретически обосновано применение этого урав­нения для сухих пород во всем диапазоне времени і. Для началь­ных стадий промачивания, когда /сЯк, скорость фильтрации и глубина I (при Н° = 0) определяются соотношениями:

Г = 2д/ЖЕ; (2.45)

Для больших периодов времени, когда /^>ЯК, становятся справед­ливыми следующие зависимости:

; v = ko. (2.43)

Как видно из формул, начальные и конечные приближения урав­нения (2.42) практически совпадают с решениями, полученными

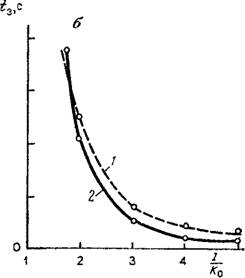
Рис. 18. Особенности инфильтрации в сухую породу.

А —влияние начальной влажности на сорбционность: / — по расчетам по формуле (2.41); 2 — по данным работы [12]; б — время образования слоя воды на поверхности при дождева­нии с различной интенсивностью: / — по данным моделирования на ЭЦВМ; 2 — ПО расчетам по формуле (2.49)

Из уравнений влагопереноса (2.39) и (2.40). Для учета начальной

Влажности следует считать Як = #'к (1 — 0). Допустимость этого

Приема подтверждается сопоставлением численного расчета S, про­веденного в работе [12], с расчетом по формуле (2.41) (рис. 18, а).

При дождевании поверхности земли с постоянной интенсив­ностью Ickо вся влага просачивается вниз. Причем если исходное увлажнение зоны аэрации соответствовало максимальной молеку­лярной влажности 0е, то скорость продвижения границы увлажне­ния можно определить в соответствии с формулой Н. Н. Бинде - мана

1 (2.47)

Где п—-показатель степени в зависимости &(0); р —-9т — 0е. При дождевании сухих пород (0е<0о) необходимо учитывать долю влаги, расходуемую на формирование связанной воды. В этом случае

7 - -во — ®е - (2.48)

А6-

^yijk о+де

При />&о в первое время слой воды на поверхности земли образо­вываться не будет, поскольку градиент высоты всасывания больше единицы. Затопление поверхности земли произойдет тогда, когда интенсивность дождя превысит скорость впитывания. Время на­
ступления режима затопления ta можно оценить, полагая, что ско­рость впитывания определяется соотношением (2.39). Тогда

ТТЩ2 • (2,49)

Рассмотренные выше закономерности подтверждаются более стро­гим анализом этого процесса, проведенным в работах Дж. Ру­бина [12].

Зависимости (2.27) и (2.49), полученные на основе простых ба­лансовых построений, достаточно хорошо описывают процесс про- мачивания при дождевании. Это, в частности, следует из сопостав­ления скорости промачивания, вычисленной по 'формуле (2.47), и данных численного анализа, проведенного Дж. Рубиным на ЭЦВМ [12]. Им рассматривалась инфильтрация при различной интенсивности дождевания рехтовского песка. Для песка харак­терны следующие показатели: 8т = 0,4, 80 = 0,005, k = 0,0133 см/с, /г = 4, Як = 15 см. По данным Дж. Рубина, при интенсивности дождя / = 1,3- Ю-3 см/с и = 5,5-10~3 см/с, при / = 3,5-10~4 см/с м = 2,5-10~3 см/с. Расчеты по формуле (2.47) дают скорости про­мачивания соответственно 5,8-Ю-3 и 2,3-10~3 см/с. В том случае, когда интенсивность дождя превышает значение коэффициента фильтрации, происходит затопление поверхности. Сопоставление времени начала затопления, полученного расчетом по формуле (2.49), и данных численного моделирования на ЭЦВМ показано на рис. 18, б. Как видно, расчеты по формуле дают вполне удовлет­ворительный результат.

Возможность образования поверхностного стока в естественных условиях можно примерно оценить, воспользовавшись зависимо­стью, приведенной в работе [7]

(2.50)

0 + 0"

Где N — число лет, в течение которых ливень, имеющий интенсив­ность I, мм/мин, продолжительностью t, мин, наблюдается в сред­нем один раз. Параметры А и В вычислены для большого числа пунктов на территории СССР. Некоторые из них приведены в табл. 18.

При орошении возможность затопления поверхности будет определяться интенсивностью до­ждевания и его длительностью. Совершенно иначе происходит инфильтрация в агрегированных породах и породах, имеющих макропоры и трещины.

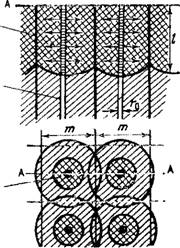
Для выяснения закономерно­стей влагопереноса в среде с макропорами рассмотрим ци­линдрический блок, по оси кото­рого проходит крупная пора (рис. 19). Учитывая пространст­венную симметрию потока, огра­ничим блок непроницаемой ци­линдрической поверхностью. Роль вертикальной миграции влаги в блоке будем считать пре­небрежимо малой, поскольку его длина значительно больше его го­ризонтальных размеров. Ё связи с этим коэффициент влагопере­носа в вертикальном направлении примем равным нулю. На по­верхности блока задается постоянный расход Q. Уравнение ба­ланса воды в канале с учетом ее поступления на поверхности земли, впитыванием в блок и заполнением макропоры можно представить в следующем виде:

(2.51)

Где /—глубина промачивания макропоры; <в' и п' — площадь по­перечного сечения макропоры и ее пористость; q — единичный рас­ход влаги, впитывающейся в блок.

В соответствии с зависимостями (2.22) и (2.23) имеем

Пт - а%

' Є •

Т

Совместное решение уравнений (2.51) и (2.52) позволяет получить глубину промачивания

(2.53)

И скорость продвижения фронта увлажнения

T

Где <в— соотношение агрегатной и межагрегатной пористостеи.

При больших периодах времени ■— «>3, скорость движения

Т

V

Фронта насыщения становится постоянной а глубина про-

Мачивания

L=u(t + x). (2.55)

При этом в зоне аэрации формируется постоянный профиль влаж­ности, смещающийся вниз параллельно самому себе. Влажность

По профилю при t ^ - -- определяется по формуле

VL

('-я

Интересно отметить, что решение (2.56) удовлетворяет линеаризо­ванному уравнению влагопереноса (2.34) при п = 1

Г>*І!§ J!? — JL-

Dzi dz dt '

«--т^. (2.57)

Где kg — экспериментальное значение коэффициента фильтрации, численно равное скорости фильтрации v. Таким образом, в случае двухкомпонентной модели среды может быть использовано урав­нение (2.34), но при этом важно учитывать зависимость обобщен­ных параметров влагопереноса от скорости промачивания.

Выше была рассмотрена схема, приложимая к зоне аэрации, имеющей одинаковую структуру до достаточно большой глубины. Распределение макропор по вертикали обычно неравномерно: наи­большее их число встречается в верхнем «активном» слое почвы, мощность которого редко превышает 1 м. В этом слое наблю­дается основная масса корней, трещин уеыхания, ходов землероев. В общем случае мощность активного слоя зависит от характера землепользования, типа и фазы развития возделываемой культуры. При конечной мощности т слоя с макропорами, что, как правило, имеет место в действительности, динамика впитывания с поверх­ности при наличии небольшого слоя на ней определяется соотноше­нием

_ —

V—-mn - і-е т (2.58)

Где т — мощность «активного» слоя или глубина наибольшего раз­вития макропор и трещин; ko — коэффициент фильтрации нижнего слоя. Учитывая практические трудности в определении мощности

«активного» слоя, целесообразно ввести параметр, характеризую­щий его общую водоемкость или его предельно возможный влаго - запас Vm, который может быть определен экспериментальным пу­тем, Поскольку активный слой достаточно макропорист, можно предполагать, что заполнение макропор происходит практически мгновенно. Тогда водоемкость слоя можно определить следующим соотношением:

(2.59)

Интенсивность потока v, идущего транзитом в более глубокие слои зоны аэрации, вычисляется в зависимости от интенсивности по­ступления влаги на дневную поверхность

(2.60)

В том случае, когда v превышает возможности поглощения влаги породами глубоких слоев, формируется поверхностный сток. В практических расчетах приращение влагозапаса AV можно опре­делять в зависимости от влагозапаса на предыдущий момент вре­мени Vj-І по формуле

(2.61)

Соотношение (2.61) дает достаточно хорошие результаты, точ­ность которых не ниже 30 % при 1.

Т

Неучет макропор может привести к существенным ошибкам в определении норм поливов. В частности, интенсивность дождя и его продолжительность должны задаваться в определенной за­висимости от ряда параметров: нижнего и верхнего пределов ув­лажнения, которым соответствуют водоємкосте активного слоя FB и Fb, поливной нормы Vn—Vv — Vn и времени влагообмена т. Не­производительные потери связаны с транзитными потоками влаги в корнеобитаемом слое в период полива.

Возможность транзитных потоков влаги отмечалась целым ря­дом исследователей. С. П. Соколовский и Г. С. Солоков приводят данные о подъеме уровня в суглинках на глубине 4—5 м через 40—50 мин после полива. При опытах с монолитами этих же су­глинков высотой 70—80 см первые порции фильтрата появлялись в нижней части в первые же минуты опыта. После искусственной кольматации пор парафином интенсивность промачивания снижа­лась в 3—5 раз. Аналогичный эффект отмечается также В. Я. Ку­ликом. Анализ данных режимных наблюдений в совхозе «Даль - верзин» в Средней Азии показывает, что подъем уровня начинается сразу же после начала полива, а спад уровня — после прекраще­ния подачи воды на поле. Анализ баланса влаги показывает, что потери на фильтрацию в период полива составили слой 0,15 м, при этом на насыщение зоны аэрации израсходовано 0,12 м. Таким

Образом, объем транзитного потока влаги равен 0,03 м, или 300 м[2]/га.

Для оценки этих потерь можно пользоваться зависимостью (2.59), считая, что изменение влагозапаса v в активном слое опре­деляется по формуле

V = (Vm-V„)( 1-е-'/т). (2.62)

Разница между поливной нормой Vn и изменением влагозапаса за время полива t и определит потери за счет транзитных потоков при условии Vn^V. Как пример можно рассмотреть возможно­сти таких потерь для южных черноземов. Время влагообмена т определено по кривым впитывания и составляет 150—200 мин. Влагозапас активного слоя, соответствующий нижнему пределу увлажнения, 114 мм (1140 м[3]/га), а для верхнего предела увлаж­нения—180 мм (1800 м[4]/га). Соответственно Vn — 60 мм (600 м3/га). В табл. 19 приводятся значения потерь в нижележа­щие слои w (мм) в зависимости от интенсивности дождевания / и принятых параметров.

Этот пример демонстрирует необходимость учета транзитных потоков в корнеобитаемом слое при обосновании норм и длитель­ности поливов. В общем случае изменение влагозапаса может следовать более сложной зависимости, чем (2.62). Определение транзитных токов при этом целесообразно оценивать по интеграль­ным кривым впитывания.

Транспирации растениями (эвапотранспирацию), принимают потен­циальную эвапотранспирацию или так называемое «климатически возможное испарение». Потенциально возможная эвапотранспира - ция Е0 различными исследователями определяется различным об­разом (в зависимости от удобства при решении географических, климатологических или агрофизических задач). В последнем слу­чае под этой величиной следует понимать максимально возможную эвапотранспирацию имеющейся растительностью в данных клима­тических условиях.

При достаточной зрелости растений транспирация составляет основную долю эвапотранспирации за счет хорошо развитого ли­ственного покрова, снижающего испарение. Поэтому во многих случаях в период вегетации растений эвапотранспирацию можно считать равной транспирации (табл. 20).

При продолжительности вегетационного периода 135 сут и при полном покрытии растениями площади расход воды на транспи - рацию составит от 270 до 600 мм или от 2 до 5 мм/сут. С учетом климата потребление влаги растениями можно опреде­лить по формуле Алпатьева [3]

Е=Кра, мм/сут, (2.63)

Где а —дефицит влажности воздуха в Па, Кр— коэффициент, опре­деляемый по биологическим кривым. Для некоторых растений ко­эффициент КР приведен в табл. 21 для условий юга Украины (по Р. А Баеру).

Величина потребления воды, представленная в табл. 20, соот­ветствует условиям полной обеспеченности растений влагой. При уменьшении влажности активного слоя увеличивается высота вса­сывания и уменьшается коэффициент влагопереноса. Вследствие этого отбор влаги корнями растений затрудняется. Анализ много­численных экспериментов, проведенный С. В. Нерпиным, В. Н. Ми-

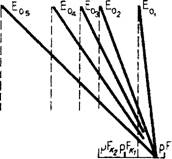
Чуриным и М. Г. Санояном, показал, что транспирация влаги расте­ниями, даже при снижении высоты всасывания, все же до некото­рого предела остается равной потенциальной транспирации. Только начиная с некоторого критического значения высоты всасывания pFfc наблюдается снижение транспирации до нуля при значении высоты всасывания pFo. Эти данные представлены на рис. 20. При pF^<pF<pF0 транспирация связана с pF линейным соотношением pF0 - pF pF0 — pF*

Поскольку pFa зависит от Eo, то уравнение (2.64) можно преобра­зовать, пользуясь данными рис. 20

Е=р (pFo — pF*.). (2.65)

При расчетах можно принимать р = 5,4 мм/сут, pFo = 4,4. Фор­мула (2.65) позволяет оценивать Е при pF>pF^.

В табл. 22 даны критические значения pF* в зависимости от по­тенциальной транспирации Ео - В этой же таблице приведены ха­
рактерные значения влажности в соответствии с зависимостью (2.7) при Як = 4 м, характерной для суглинков. При этом pF*. может быть рассчитано по формуле (2.65)

PF*=pFo-------

Из табл. 22 следует, что для наиболее часто встречающегося диапазона величин суточной потенциальной транспирации крити­ческой высоте всасывания соответствуют чрезвычайно низкие зна­чения влажности завядания.

Для практических расчетов расходование влаги при постоян­ных во времени метеоусловиях можно считать постоянным (Е = — Е0), пока влажность не достигнет значения 03, ниже которого испарением можно пренебречь, считая Е = 0.