ГИДРО­ГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ

Стационарные потоки в зоне аэрации

Анализ режима влажности в естественных условиях и при оро­шении позволяет выделить в зоне аэрации три области. Первая область ниже активного слоя — область переменной влажности — имеет мощность от 2 до 6 м. Колебания влажности в ней связаны с сезонными изменениями в поступлении и расходовании влаги в верхнем активном слое. Мощность этой зоны зависит от периода колебания влажности и фильтрационных свойств пород. Для ори­ентировочной оценки глубины, где колебания влажности затухают, можно воспользоваться решением уравнения (2.34) при п — І для случая, когда влажность на границе меняется по закону синуса [40]. Из этого решения следует, что колебания влажности затухают При z>0,2t0k0. Так, для годового цикла колебаний влажности эта глубина составит для песков 10—30, для супесей 5—10, для су­глинков 2—3 м. Такие же колебания испытывают и расходы влаги. В верхней части зоны аэрации сезонные изменения интен­сивности влагопереноса выше, а с глубиной они уменьшаются. Этим, в частности, объясняется уменьшение амплитуды колебания уровня с увеличением глубины залегания. Причем уменьшение амплитуды свидетельствует не об уменьшении питания с глубинои, а только о его стабилизации во времени. Ниже области перемен­ного увлажнения находится область транзита, где влажность в те­чение длительного периода времени практически не меняется и со­ответствует значению влажности, определяемому средне-многолет­ним значением питания подземных вод w. При использовании зависимости (2.11) эту влажность можно определить по формуле

(2.67)

Соответственно при известных 0 и можно определить интенсив­ность питания подземных вод

W=k0Qn.

Зона транзита примыкает к капиллярной кайме, где колебания влажности связаны с изменением уровня подземных вод. Режим влажности здесь обусловлен режимом уровня подземных вод и мо­жет иметь хорошо выраженную периодичность.

В естественных условиях приток к поверхности подземных вод компенсируется оттоком к естественным дренам, что определяет относительную стабильность уровня подземных вод, особенно при большой глубине их залегания. Распределение влажности по вы­соте над уровнем подземных вод находится в зависимости от гид­рофизических характеристик пород зоны аэрации k (t|>) и ф (0) и интенсивности потока влаги v. В общем случае высота 2, для ко­торой характерно значение высоты всасывания - ф, определяется по

Формуле *

Z=\.—-BL----------------------------------------------------------------------------------------------------- (2.69)

OJ 1 - 1

Значение z вычисляется численным интегрированием при известной функции Если может быть представлена простой функ­цией, то проблема упрощается. Например, при

А=Аое~№ (2.70)

І __ е-Р*

Ko

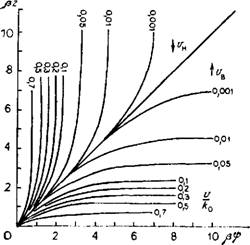
Для других зависимостей k (ф) решения уравнения (2.69) можно найти в работе [31]. График зависимости Pf от рг при различном соотношении vjko показан на рис. 21, а. При отсутствии потока в зоне аэрации высота всасывания - ф в каждой точке соответст­вует высоте над уровнем подземных вод. При питании (г><0) ■ф<2, а при восходящем потоке (v < 0) 'Ф > г. Эти особенности, в частности, могут служить для определения направления потока влаги в зоне аэрации. Зная зависимость ^{z), можно построить соответствующие графики распределения влажности в зависимости от интенсивности расхода и направления потока. На рис. 21, б по­казан такой график, построенный с использованием функции 0 = = При о = 0 распределение влажности определяется рав­

Новесной кривой, соответствующей зависимости - ф (0), при условии положения начала координат на свободной поверхности подзем­ных вод. При нисходящих потоках влаги эпюры влажности распо­лагаются правее равновесной кривой, а при восходящих потоках влаги — левее ее.

В неоднородной зоне аэрации высота всасывания в каждом слое будет определяться в зависимости от функции £(-ф). Причем при отсутствии потока влаги в зоне аэрации линейная зависимость между высотой всасывания и высотой над уровнем сохраняется.

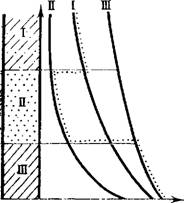
Рис. 22. Равновесное распределение влажности в слоистой системе. Циф­ры у кривых определяют принадлеж­ность зависимости к тому или иному слою, а точки — равновесное распре­деление влаги

Однако при этом распределение влажности в каждом слое будет определяться зависимостью г|)(0), характерной именно для этого слоя, а на границах слоев будут наблюдаться скачки влажности, как показано на рис. 22.

При нисходящих и восходящих потоках влаги зависимость вы­соты всасывания от высоты над уровнем уже не будет опреде­ляться гладкой непрерывной функцией, а графики (z) на грани­цах слоев резко преломляются. При этом должно соблюдаться условие

0+1- <"2>

Где индексы 1 и 2 определяют принадлежность высоты всасывания и зависимости k (ф) тому или иному слою. В зоне транзита, где

— 0, влажность будет определяться в каждом слое по фор-

Az

Муле (2.11) в зависимости от параметров данного слоя.

Закономерная многолетняя тенденция в подъеме уровня или его спаде чаще всего связана с хозяйственной деятельностью чело­века. В зависимости от характера процесса, его направленности и интенсивности в зоне аэрации происходит переформирование про­филя влажности, затрагивающее либо всю зону аэрации, либо про­являющееся только в капиллярной зоне.

Для анализа этих явлений рассмотрим зону аэрации такой большой мощности, чтобы можно было бы не учитывать периодиче­ские изменения влажности в верхней области.

Примем зависимость коэффициента влагопереноса от линейной влажности в соответствии с формулой (2.11), а между влажностью и высотой всасывания ф — экспоненциальной (2,8).

Как было показано ранее, при принятых зависимостях уравне­ние влагопереноса можно привести к линейному

KoHк + = (в/л — во) • (2.73)

Полагая, что по истечении некоторого времени режим влагопе­реноса в зоне аэрации становится квазистационарным и профиль влажности перемещается параллельно самому себе с некоторой по­стоянной скоростью и, зависящей от граничных условий, введем новую переменную % — z — ut и преобразуем уравнение (2.73)

, „ т. . аё ае _

+ = -(9«-во) и-Щ-. (2-74)

Решим его для зоны аэрации достаточно большой мощности. Бу­дем считать, что при о скорость влагопереноса определяется интенсивностью среднего питания /0. На свободной поверхности возможен ОТТОК V, в связи с этим граничное условие при £ = 0 бу­дет иметь вид аё

KoHK~~k0 = v. (2.75)

Кроме того, при I = 0 наблюдается полное насыщение пород

(8=1). Решение уравнения (2.74) при принятых граничных усло­виях имеет вид

О _ - I + V ехр (-Ц^Л + ^ZJL, (2.76)

1+Мо" V / 1+ИМ0 7

Где

— о — и т - / — I -4- v v = -.— ; и = —-; / = г ; « = —,

«о k0 k9 ( J _ / )

V положительно при подпитывании зоны аэрации из грунтовых вод и отрицательно при дренировании. Рассмотрим некоторые частные случаи.

1. При отсутствии питания, оттока или притока к свободной по­верхности со стороны подземных вод их уровень будет стабильным.

Распределение влажности по высоте над уровнем будет опреде­ляться в соответствии с зависимостью (2.8)

0 = ехр (-—-). (2.77)

При этом в каждой точке зоны аэрации соблюдается равенство f ==z.

2. При наличии питания, интенсивность которого I постоянна во времени, распределение влажности будет зависеть от возмож­ности оттока от свободной поверхности. В том случае, когда отток отсутствует (у = 0), уровень будет подниматься. Распределение влажности по высоте над уровнем будет иметь вид

0 = - T-lr - ехр (-£ + jL.. (2.78)

1 — V ъ Як / 1 — uuo '

С удалением от уровня влажность стремится к некоторому значе­нию 0 = 7. Недостаток насыщения р, при этом также определится в зависимости от

Ц = цоО— Т). Скорость подъема уровня постоянна

— м - *

3. Отток от свободной поверхности v = I. В этом случае дви­жения свободной поверхности наблюдаться не будет и £ = 0. Из­менение влажности по вертикали будет определяться следующим соотношением:

0= (1 +й) ехр—+

При водопонижении или при подпоре подъем или спад уровня обес­печивается только потоком от свободной поверхности. В этом слу­чае распределение влажности по высоте над уровнем описывается

V

Уравнением (2.76) при и = ----------

Ро

При достаточно большом удалении от свободной поверхности

Влажность стремится к наименьшей влагоемкости 0->-0о; 0 = 0. Изменение уровня происходит с постоянной скоростью

_ V

~~ !*о *

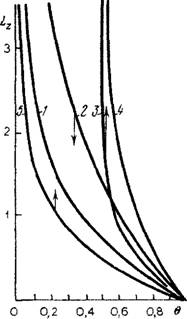
На рис. 23 показаны кривые распределения влажности над уровнем подземных вод, соответствующие рассмотренным случаям. Анализ этих примеров дает основание для построения схемы питания под­
земных вод и осушения и насыщения зоны аэрации большой мощности. Эта задача возникает на орошаемых масси­вах в связи с прогнозом подъема уровня при изменении интенсивности питания подземных вод при орошении. При этом можно выделить два периода. Первый период — промачивание зоны аэрации. Его длительность t\ определяется по формуле

JV"We + Aw - ^wo )

(2.79)

Aw "/ ko

Где we — питание подземных вод в есте­ственных условиях; Aw — приращение литания за счет орошения; L — глубина до уровня воды. Для примера рассмот­рим зону аэрации мощностью 10 м, сло­женную суглинками с коэффициентом фильтрации &о = 0,1 м/сут, п = 4 и недо­статком насыщения fio = 0,2. Питание в естественных условиях примем 40, а приращение питания Aw — 60 мм/год, или 20 % от поливной нормы 3000 м3/га. Расчет по формуле (2.79) дает значение t\ — 0,5 лет, что соответствует наблю­даемому в действительности. Обычно подъем уровня при такой мощности зоны аэрации происходит в течение года или полутора лет после начала орошения. Для вто­рого периода характерно монотонное повышение уровня, темп ко­торого определяется приращением питания Aw, недостатком на­сыщения рн и условиями естественного дренирования, определяю­щими отток от свободной поверхности vg. Скорость подъема уровня определяется по формуле

Dh AW - Vg

Dt |лн '

Где рн в зависимости от приращения нитания равно

F^W-)-

Рассчитанное таким образом значение рн может быть значительно меньше ро и обычно меняется от 0,05 до 0,15.