ГИДРО­ГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ

Скважины

Специфика моделирования скважин на сплошных моделях разобрана достаточно подробно [17]. Применительно к сеточным моделям плановых потоков (а также на ЭЦВМ) существуют чет­кие и обоснованные рекомендации для задания одиночных сква­жин в центре квадратных и правильных многоугольных блоков [17]. Эти рекомендации основаны на представлении о радиальном характере потока в скважинном блоке, что дает возможность опре­делить общее сопротивление потока между скважинным блоком и соседними блоками, задавая вокруг скважины круговой контур питания радиусом, равным шагу сетки с центром в скважине. Та­кая расчетная схема приводит к следующему соотношению между напором в скважине Яс и скважинном блоке Я:

(3.25)

Где о—расчетный шаг сетки; А — параметр, зависящий от струк­туры сетки.

Для квадратной сетки при а = Ал; = А// в выражении (3.25), полученном различными путями [17], параметр А изменяется в не­больших пределах 1,57—1,62, причем для практических расчетов рекомендуется экспериментально обоснованное значение Л = 1,62. Для прямоугольной сетки выражение для Ф°с дал П. Ниллерт [46],

Анализируя средний потенциал внутри скважинного блока, а Д. Притчетт и С. Гарг [48] получили аналогичные результаты по экспериментальным данным для одиночной скважины и для сетки скважин. Численный анализ этих результатов показывает, что для прямоугольной сетки также можно определять величину Фс° по формуле (3.25) при А = 1,62, принимая

О = У675 (д*2 + д¥)• (3-26)

При эксцентричном расположении скважин (сдвинутых относи­тельно центров блоков) для квадратной сетки ГЇ. Ниллерт [46] ре­комендует расчетный прием, согласно которому каждый соседний со скважиной узел получает часть расхода скважины, определяе­мую по специальным таблицам, полученным эмпирическим путем. Недостатком этого способа является увеличение числа узловых точек, в которых задается расход скважин, а также осложнения с переходом от напора в узловых точках к напору в самой сква­жине.

Ниже излагается более простой способ решения этой задачи, который основан на предположении, что эксцентричная скважина сносится в ближайшую узловую точку, вводятся поправки в фильт­рационное сопротивление Ф° и в напоры, получаемые в окружаю­щих узлах.

Для квадратной сетки при таком подходе фильтрационное со­противление между соседними узловыми точками и скважиной мо­жет быть определено, задавая круговой контур питания, проходя­щий через соседние узловые точки, как это сделано для случая расположения скважины в узловой точке [17, 38]. Используя ре­шение для эксцентричной скважины в круговой области, можно показать, что выражение для дополнительного сопротивления в скважинном блоке здесь определится так же, как и при централь­ном расположении скважины, но с заменой шага квадратной сетки а — Дх = Ау на величину а0, причем

Г2

Ао^а--!, (3.26а)

Где го — расстояние от скважины до центра блока (рис. 43, а).

Кроме того, в понижения напора, определенные в соседних со скважинным блоком узлах, следует добавить (со своим знаком) по­правку А5Экс на эксцентричность скважины, определяемую выра­жением

Где г° — расстояние между узлами блоков, в которых находятся скважина и расчетная точка; г — расстояние от скважины до рас­четной точки (узла или другой скважины).

Этот же расчетный прием можно распространить на прямо­угольную сетку (при А* Ф Ау). В этом случае для учета эксцент­ричности скважины в блоке при расчете величины о в (3.25) Ах

ЕВ? ПЪ Dl]j

Рис. 43. Расположение эксцентричной скважины в квадратной (а) и прямо­угольной (б) сетках.

1 — границы блоков; 2 — узлы сетки; 3 — сКважииы; 4 — расчетные точки

И А у заменяются величинами Ал;' и Ayf, определяемыми выраже­ниями

(3.28)

Где гх и гу — проекций расстояния от скважины до центра блока (рис. 43, 6). При этом поправка ASaKc определяется тем же выра­жением (3.27).

Для проверки погрешностей рекомендуемых способов задания эксцентричной скважины на сеточной модели То Ван Нью прово­дил тестовое моделирование для стационарного потока в квадрат­ной области при квадратной и прямоугольной сетке, данные кото­рого показали, что при предлагаемом способе реализации скважины значения погрешностей в определении скважинного сопро­тивления Ф° , как правило, не превышали 1 % и только при рас-

Положении скважины посередине между узловыми точками дости­гали 2—2,5%, а погрешности в определении потенциалов находи­лись в пределах до 3 %. Примерно такие же погрешности (даже несколько больше) получены при реализации скважин по способу П. Ниллерта.

Предлагаемый прием распространяется и на случай расположе­ния в блоке нескольких эксцентричных скважин, которые заме­няются укрупненной эквивалентной скважиной («большим колод­цем») радиуса гк

Гк = У (01°2> •••> а'п-дгс,

Где ог— расстояния от скважины номера і до расчетной скважины

Номера п с радиусом гс. При этом расчетный шаг квадратной сетки определяется выражением (3.26а) при расположении эквива-

Лентной скважины в центре системы скважин данного блока, а по­правки А5Экс определяются по формуле (3.27) от действия каждой скважины в соседних блоках, а затем суммируются.

Особого подхода требует также обоснование сеточной схемы для берегового водозабора, представляющего собой ряд скважин, располагаемых вдоль берега реки (водоема). Тестовое моделиро­вание, проведенное То Ван Нью, показывает, что в этом случае сле­дует задавать узловые точки так, чтобы они совпадали с контуром скважин, причем сетку вблизи водозабора можно делать прямоли­нейной с вытянутыми вдоль линии скважин блоками, ориентиро­ванными по направлению водозаборных линий.

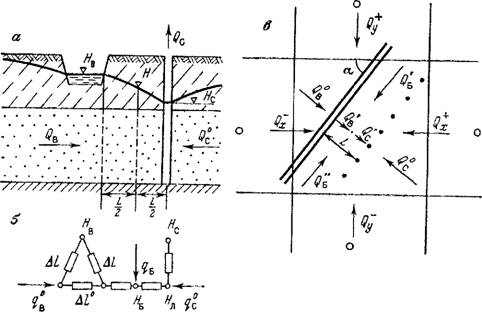
При близком расположении береговых скважин к водотоку не­редко не представляется возможным сделать столь подробную раз­бивку, чтобы между водотоком и скважиной располагался хотя бы один блок, и тогда береговые скважины оказываются в одном блоке с водотоком (рис. 44). Приведем обоснование сеточной мо­дели при наличии вблизи водотока, гидравлически связанного с по­током грунтовых вод, ряда береговых скважин, когда в блок попа­дает не менее двух скважин, располагаемых от водотока на рас­стоянии L ^ о.

В общем случае ложе водотока моделируется системой сопроти­влений АФ и АФ°, соединяемых по схеме треугольника [17], а расход скважин Q связывается с напором в скважинах Нс соот­ношением (3.2), реализуемым введением дополнительного сопротив­ления Фкс = LKJNT. Для упрощения такой системы сопротивлений
пренебрежем за малостью расстоянием L между водотоком и сква­жиной, а также внешним притоком к водотоку. Тогда эта система заменяется одним сопротивлением Фвс, на конце которого задается напор Явс, причем величины Фвс и Явс находятся из соотношений:

+ (3.30)

,, ЯВФкс + ЯСАФ* ,0 „Л,

= (3-30й)

Если заданным является дебит скважины, то сопротивление Ф„С может быть произвольным, оно должно только обеспечивать задание в блок тока, соответствующего расходу скважин в блоке.

После проведения моделирования расчеты потока между водо­током и скважинами делают аналитическим путем. Для этого пред­варительно по данным моделирования находят расходы потоков в блоке и определяют их проекции Q-, Q+, Q-, Q+ на напра­вление нормали к линии водотока со скважинами, которые дают расходы внешнего притока—оттока на линии водотока 0° и на ли-

Нии скважин Q0

^ с

= Qx sin а + Qy cos «• Qc = Qt sin а + Qy cos «»

A также проекции расходов на направление вдоль водотока и ли­нии скважин, которые дают расход Qe, поступающий внутрь блока между водотоком и линией скважин

Q6 = Q'6 + Ql = (QJ + Q+) COS a + (Q - + Q+) sin a. Соответствующие удельные расходы q°B = Q° jN, q°c=Q°cfN

И qs == Q6fN вводятся далее в аналитический расчет системы водо­ток—скважина по схеме, приведенной на рис. 44, б, причем расход бокового притока q$ считается проходящим посередине между ря­дом скважин и водотоком. Тогда баланс притока в каждой внут­ренней узловой точке дает возможность составить уравнения, свя­зывающие удельные расходы потока с напорами Ял, Яб, И' ,

Л В

Я;'в . Исключая из этой системы уравнений напоры Н'пъ и Я"в,

После алгебраических преобразований получаем уравнение, связы­вающее напоры Ял и Я б

ТГ*-' (3'3,>

Где q6 = q6/T, q°B = <7® /Т, а AL, AL° и AL* — параметры (экви­валентные длины потока) сопротивлений АФ, АФ° и АФ* (AL = = 7WАФ; AL° — TNАФ°; AL* = TNАФ*).

Другое соотношение между Ял и Яб получаем из уравнения баланса потока в узле с напором Ял

(3.32)

Где

ЯІ-йЦТ', qc = qjT — Qc/aT,

Дальнейшее преобразование этих уравнений зависит от того, что является заданным для скважин — дебит или напор. Если за­даны дебит и расстановка скважин, то известно qc. Тогда, подстав­ляя Я л — Яб из (3.32) в (3.31), получим

Яб= нв~ (AL* + 0,5L) (<7С+ q6-дГЯ^Р'^' (3-33)

Если же задан напор в скважинах Яс, то величина qc в (3.32) выражается из (3.2), и тогда

"'-"•--ЕЙг^-^}

Подставляя это выражение в (3.31), после преобразований получим

„ (AL*+0,5t) (£кс+0,5I)

„ . AZ. AL* _о

Яв + 1ГТД7<?в Яс + ^кс _ _ ДІ* + 0,5£ + LKC + 0,5L 46.

После определения Яб из (3.33) или (3.34) из (3.32) или (3.33а) найдем Ял — Яб, после чего получим расходы q' =

==2Г(Яб —Ял)/1 и а также напор #J, C =

= ЯбЧ—п0 которому следует проверять сохранение гидрав­лической связи между водотоком и фильтрационным потоком. При необходимости можно, кроме гого, рассчитать напор Я^в по фор­муле

ALM0 (_ яв Ялв ^ лв " Ж+ Ш + дг ■+ AL0 (3.35)

Длят оценки достоверности предлагаемой методики То Ван Нью была решена тестовая стационарная задача при различном распо­ложении водотока и ряда скважин в блоке, на основании которой можно судить о хорошей точности предлагаемого приема модели­рования.

При расчетах систем скважин вертикального дренажа в плано­вом потоке целесообразно использовать методику, основанную на модельном определении единичных функций, позволяющих рассчи­тать понижение напора от действия каждой скважины по выраже­нию (3.12). Техника определения единичных функций на сплошных и сеточных моделях описана в [17].

Следует иметь в виду, что при работе скважин в безнапор­ных потоках может образоваться столь значительное понижение уровня в скважине, при котором вблизи нее уже нельзя считать неизменной проводимость пласта, хотя в зонах, удаленных от сква­жин, проводимость пласта практически остается постоянной. В таком
случае расчеты и моделирование можно осуществлять при постоян­ной проводимости, а получив таким путем расчетное понижение напора в скважине, следует перейти к действительной глубине воды в скважине, учитывая уменьшение проводимости пласта на основании общих правил связи зависимостей при различном строении плановых потоков [17, 38].