ГИДРО­ГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ

РАСЧЕТЫ ГОРИЗОНТАЛЬНОГО СИСТЕМАТИЧЕСКОГО ДРЕНАЖА ПРИ СТАЦИОНАРНОМ ИНФИЛЬТРАЦИОННОМ ПИТАНИИ

Основные расчеты линейного систематического дренажа (ли­нейного и площадного) производятся при равномерном стацио­нарном площадном питаний. При этом в качестве исходного при­нимается условие поддержания заданного уровня грунтовых вод между дренами.

Как следует из обоснования геофильтрационной схематизации (см. гл. 1, § 3), в качестве типовых расчетных схем строения по­тока по вертикали примем: 1) однопластовую схему, которая в за­висимости от отсутствия или наличия покровных отложений может иметь однородное или двухслойное строение (см. рис. 35, а, б), и 2) двухпластовую схему соответственно трех - и четырехслойного строения (рис. 46). Такая типизация строения водоносных отложе­ний (отдельно по количеству пластов и по количеству слоев) при­нята в связи с тем, что общие условия формирования фильтраци­онного потока между дренами (а вместе с тем и общее построение расчетных зависимостей) определяются количеством водоносных пластов, а гидродинамическое несовершенство дренажа зависит, кроме того, от строения водоносного комплекса (характеристик покровного и разделяющего слоев).

Расчетная интенсивность площадного питания w в однопласто - вой системе складывается из интенсивности инфильтрационного питания оросительными водами w0, определяемой по данным вод - нобалансовых исследований (см. гл. 2, § 2), и из интенсивности «напорного» питания wH, поступающего из нижележащих горизон­тов. В двухпластовой системе целесообразно разделять эти вели­чины, считая расчетную интенсивность площадного питания в верх­нем пласте Wi = w0, а в нижнем пласте w2 = wH, причем величины wH, как правило, следует определять по данным регионального мо­делирования.

Рис. 46. Двухпластовая схема строения по­тока по вертикали:

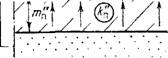
1 — трехслойная, когда дрена вскрывает первый водоносный пласт; 2 — четырехслойная, когда дрена находится в покровных отложениях

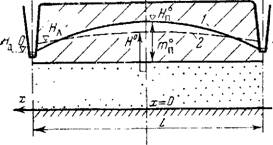
Рис. 47. Систематический горизонтальный дренаж в однопластовой системе:

А — сечение потока поперек дрен; б — фрагмент потока у дрены при наличии экранирующего слоя в покровных отложениях; !—уровни свободной поверхности; 2 — напоры в основном пласте

А

I И I I I I И I?

При построении расчетных зависимостей для глубоких горизон­тальных дрен, располагаемых на значительных расстояниях L друг от друга, как правило, можно принимать на междудреньи поток плановым с постоянной проводимостью, а несовершенство дренажа учитывать введением локального сопротивления по соотношениям, приведенным в разделе 1 настоящей главы. Как показывают ре­зультаты тестового моделирования для однопластовой системы, та­кой подход реально применим, если общая мощность дренируемого пласта т не превышает 0,25L. В противном случае при расчетах следует считать водоносный пласт неограниченным по мощности.

В однопластовой системе (рис. 47) для основного рас­четного случая (при m<0,25L) связь напора на междудреньи Я• и на линии дренажа Ял устанавливается приведенными в [13, 38] уравнениями симметричного инфильтрационного потока. На осно­вании этих уравнений, принимая плоскость сравнения на уровне воды в дрене (Яд = 0), запишем формулу для определения рас­стояния между дренами в виде

1 = + (3.46)

При наличии покровных отложений величина напора Я0 в се­чении посередине между дренами может заметно отличаться от
уровня поверхности воды в покровном слое Н°п за счет потери на­пора на перетекание инфильтрадионного потока в покровном слое, определяемого по выражению = wm° Jka. В однородном

Пласте глубиной h° эту разницу напоров (среднего по пласту и на свободной поверхности) можно определять из того же выражения, заменяя т°п на h0/3, где h° — глубина потока посередине между

Дренами.

Для расчетов систематического комбинированного дренажа в формуле (3.46) следует считать 1д = £Кд, причем величина LKд определяется по формуле (3.7), а плоскость сравнения напоров за­дается на уровне расчетного напора комбинированного дренажа, определяемого по формуле (3.7а). Для расчетов прерывистого дре­нажа следует принять 1д = 1пд, определяя ІЦД по формуле (3.8). При необходимости учета притока по длине горизонтальной дрены прерывистый дренаж должен рассчитываться как комбинирован­ный, причем расчетная длина 1кд для такого дренажа определяется формулой (3.7), в которой заменяется L^c на £пд, a LнД опреде­ляется для горизонтальной дрены без учета «окон».

Как показывает решение тестовых задач на моделях ЭГДА, та­кие расчетные зависимости применимы, если мощности пластов (водоносного и покровного) не превышают величины 0,21. Если эти условия не соблюдаются, то для расчета следует использовать зависимости, применимые для схемы пласта неограниченной мощ­ности [1, 14J.

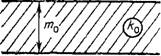
Значительное влияние на работу горизонтального дренажа мо­жет оказать строение покровных отложений и, особенно, содержа­ние в них слоев, представленных тяжелыми глинистыми разно­стями. При одном порядке значений коэффициентов фильтрации слоев учет слоистости можно произвести, вводя приведенную мощ­ность покровных отложений тт по отношению к проницаемости, в котором располагается дрена

П

(3.47)

Где ГПі и ki — мощности и коэффициенты фильтрации t'-ro слоя, a k\ — расчетный коэффициент фильтрации, задаваемый для верх­него слоя (на уровне дрены). Возможность применения такого при­ема подтверждалась результатами моделирования дренажа в слои­стой системе, однако большой диапазон возможных условий не по­зволяет четко установить его оптимальные границы, так что в каждом случае он требует подтверждения тестовым моделиро­ванием.

Особое значение следует придавать слабопроницаемым слоям небольшой мощности, залегающим вблизи дрены, имея в виду, что даже слои мощностью порядка 0,1 м при коэффициентах фильтра­ции порядка 0,001—0,01 м/сут могут иметь принципиальное зна­чение, особенно при малых междудренных расстояниях.

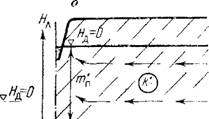
Нередко в основании покровных отложений имеется относи­тельно слабопроницаемый слой, в частности, оказывающий экрани­рующее влияние на поток под дреной. Рассмотрим одномерный ста­ционарный в плане поток вблизи горизонтальной дрены при нали­чии такого экранирующего слоя (см. рис. 47, б), принимая поток в экранирующем слое вертикальным и в верхнем слое горизонталь­ным, а в подстилающем водоносном пласте считая напор Ял неиз­менным.

Тогда распределение напоров Я в верхнем слое представляется дифференциальным уравнением перетекания

' ФН,,» я,-// .

+ К ----- г--- -0, (3.48)

От­

Решение которого в слое неограниченной длины имеет вид

(3.49)

Где Я° — средний напор на линии дрены (при х = 0). Учет гидро­динамического несовершенства дрены в верхнем слое производится по методу локальных сопротивлений, согласно которому удельный приток в дрене qn связывается со средним напором Я° при

Яд = 0 соотношением Я0

<7д = *Х-7Г-> (3-50)

Нд

Где 1°нд — параметр несовершенства дрены в верхнем слое, кото­рый при однородном строении верхнего слоя и отсутствии входных сопротивлений дрены определяется по формуле (3.1а) при т = = тг.

П

Расход дрены получим дифференцированием уравнения (3.49)

_п = (Я - Я®) V (3.50а)

Сопоставив выражения (3.50) и (3.50а), исключим из них Я° , после чего получим

Нл-н°д=-------- - Л-Т(Г-, ------- —п~ (3-51)

1+2* А Д "0,5 + М<нд

Отсюда получается выражение для параметра несовершенства дрены 1Нд по отношению к основному пласту проводимостью Т

П'"п

Пример расчета. Дрена с расчетным диаметром йд=1,05 м располагается в покровных отложениях мощностью (под дреной) тп=5 м с коэффициентом фильтрации 0,5 м/сут; проводимость подстилающего пласта Г» 150 м2/сут.

По формуле (З. Іб) находим параметр сопротивления на несовершенство дренажа

^«0,73^18 5-^^- 240 м.

При а>=10~3 м/сут и Н°=1,5 м по формуле (3.47) получим расстояние между дренами

150"

[д/2402 + '25° jQ-f - - 240J == 690 м.

Рассмотрим теперь влияние залегающего в основании покровных отложе-

//

Ний слабопроницаемого слоя мощностью тп =0,5 м с коэффициентом фильтра - tt

Ции kn =0,01 м/сут. Проведем расчет величины Laд по формуле (3.51а) при /гп =0,5 м/сут и тп = 4,5 м, вычисляя предварительно согласно (3.16),

2 • 4,5

^нд = 0,73 ■ 4,5 lg 3 fH/105 =1.5 М и Тогда

= 0,515Q4,5 (ТТW + 1>5) = 470

Что при тех же условиях дает расстояние между дренами L = 430 м. Как видно, наличие слабопроницаемого слоя требует здесь значительного умень­шения расстояния между дренами.

Значительное влияние на работу дренажа оказывают также маломощные хорошо проницаемые слои, расположенные в непо­средственной близости от дрены. Это положение подтверждают ре­зультаты моделирования работы дренажа в толще суглинков мощ­ностью 50 м с коэффициентом фильтрации 0,1 м/сут, содержащей песчаный прослой с коэффициентом фильтрации 5 м/сут. На мо­дели оценивался напор между дренами с расстояниями L = 100 м и w = 2-10~3 м/сут при различных положении и мощности песча­ного прослоя; результаты решения задачи приведены в табл. 35.

Как видно из этих данных, особое значение следует придавать таким песчаным прослоям, которые залегают в пределах глубины дренажа, причем в этом случае в первую очередь важно установить

Сам факт присутствия такого слоя, поскольку его мощность не имеет принципиального значения.

С углублением слоя под дрену картина резко меняется, и ра­бота дренажа становится затрудненной, а при некоторой глубине залегания слоя его наличие не сказывается на фильтрации к дрене.

Для линейного систематического дренажа в двухпласто - вой системе вывод расчетных зависимостей приведен в прил. 1. В этом случае напор Н'0 в верхнем пласте между дренами опреде­ляется уравнением (13) прил. 1, причем величина L' представляет

Собой параметр несовершенства дрены по отношению к верхнему пласту (т. е. считая разделяющий пласт водоупором). При условии

Двухпластовая система может рассматриваться как однопластовая, причем из выражения (14) прил. 1 следует, что в этом случае рас­стояние между дренами может определяться по формуле (3.46) при параметре несовершенства дрены

- Ж, + ТГ 4 » ~ Л/І^П - Т = ^ + <3-53>

Выражение (3.53) можно распространить и на многослойные пла­сты. Покажем путь такого решения на примере трехпластовой си­стемы, в которой добавляется нижний пласт проводимостью Т3 с разделяющим слоем мощностью mf0 и коэффициентом фильтра­ции k'Q. В этом случае можно считать величину LK по формуле (3.53), заменяя в ней //д на L", равную 1д для двух верхних пла­стов (при Т = Т] + Т2), а при определении коэффициента перетека­ния Т на Ті + Т2+Тз, Ті на Тг + Т2, Т2 на 7s, kQ на k'Q и m0 на m'0,

Т. е. получим

Г __ .__ ______ Тз_ __ і Ті 4- Т» 4- Тз г"

* 2 (Ті 4- Т2) Ь' Т\ 4- Т2 д'

V %(Т\ + Г2)Г3

При этом должно выполняться также условие для Ь = Ь'.

В частности, для условий монотонного чередования водоносных слоев с одинаковой проводимостью km и слабопроницаемых раз­деляющих слоев с одинаковыми значениями удельных сопротивле­ний rripfkр общий параметр сопротивления несовершенства дренажа определяется по формуле [28]

І VІ (І — 1)

Kp

ШБ7' (З-54*)

Где L' — сопротивление дренажа относительно 1-го слоя, ад — д

Число пластов. Для двух пластов f2 — 0,36, для трех /з = 0,5, для пяти f5 — 0,61, при большом числе пластов можно считать fn = = too = 0,79.

Рассмотренный выше критерий применим и к анализу ситуации, когда фильтрационные свойства пластов различны. Исследования показывают [28], что при расчетах дренажа в слоистбй толще не­редко достаточно рассматривать только первые два пласта.

При рассмотрении потоков большой протяженности вертикаль­ные сопротивления, возникающие за счет наличия в разрезе слабо­проницаемых слоев, можно не учитывать при L > 6п/Ь. Это дает возможность при прогнозах изменения уровня на больших терри­ториях схематизировать поток как плоский в плане.

В тех случаях, когда дрена находится в покровных слабопро­ницаемых отложениях, нередко оказывается Ln^>L. При этом в формуле (3.9) можно считать = и принимать Ьвд из (3.16), так что выражение для напора между дренами примет вид

Но — //д 0,73 ig, (3.55)

В котором напор между дренами не зависит от фильтрационных свойств водоносного горизонта. В многопластовых системах при наличии покровного слоя вероятность такой ситуации еще выше, поскольку сопротивление дрены увеличивается за счет влияния слабопроницаемых слоев.

Из анализа работы дренажа в слоистых системах следует, что основное внимание при исследовании должно быть обращено на изучение верхней части разреза, особенно покровных отложений. Глубина исследований зависит от положения в разрезе второго водоносного горизонта. При большой мощности слоя, разделяю­щего два пласта, определяющую роль будет играть только первый пласт, на изучении которого и следует сконцетрировать внимание.

Одной из расчетных схем, учитывающих подпитывание дренажа из нижележащих пластов, является схема «напорного питания» [1], в которой принимается, что при работе дренажа остается не­изменным исходный напор в пластах, подпитывающих первый от поверхности водоносный пласт. Для определения напора посере­дине между дренами в этом случае можно пользоваться уравне­нием (25) прил. 1. Однако эта расчетная схема является чрез­мерно жесткой и ее использование может быть оправдано только при учете подпитывания из глубоких горизонтов дренажа неглубо­кого заложения.