ГИДРОГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ
Параметры влагопереноса
Для характеристики движения влаги используются понятия об объемном единичном расходе или, как его принято называть, плотности потока — характеристике, аналогичной скорости фильтрации при полном насыщении. Согласно закону Дарси—Клюта, скорость фильтрации v определяется градиентом напора Я и коэффициентом влагопереноса к
Р.4)
При полном насыщении пор водой коэффициент влагопереноса к соответствует коэффициенту фильтрации пород ко. Величина напора в данном случае определяется в соответствии с уравнением Я. Бернулли
// = -£-+*, (2.5)
Где г — ордината точки над плоскостью сравнения; р — давление; у — объемная масса воды.
Чаще для характеристики напора используется пьезометрическая высота.
В условиях неполного насыщения пород аналогом давления является давление всасывания, удерживающее воду в породе капиллярными силами, зависящими от кривизны поверхности раздела на границе воды и воздуха, и сорбционными силами, определяемыми молекулярным взаимодействием воды и скелета породы. Иногда в качестве единицы используется десятичный логарифм высоты всасывания, выраженный в сантиметрах водяного столба. Он обозначается символом pF. Полученная таким образом высота всасывания г|) будет характеризовать силы, удерживающие воду в не полностью насыщенной породе.
|
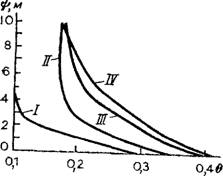
Рис. 10. Зависимость высоты всасывания от влажности для некоторых пород. |
/ — супесь легкая; // — средний суглинок; ///—лёссовидный суглинок; IV — тяжелый суглинок
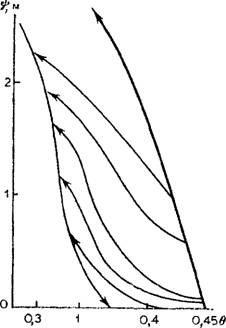
Рис. 11. Зависимость t|)(#) для тяжелого сыртового суглинка из Куйбышевской области. Стрелки, направленные в сторону увеличения влажности, определяют увлажнение, а в сторону уменьшения — осушение
|
|
Для ненасыщенных пород формулу для напора можно записать в следующем виде:
Высота всасывания при полном насыщении равна нулю. С уменьшением влажности высота всасывания возрастает по абсолютной величине, достигая 100 м и более в сухих породах.
Зависимость высоты всасывания от влажности (8) в различных породах разная и определяется экспериментальным путем. Пример такой зависимости для песков, супесей, суглинков и глины показан на рис. 10. Для некоторых практических расчетов эту зависимость удобно представить в виде следующих соотношений:
4> = 2//к(1 -0) + /-/(>; (2.7)
= —Нк In 0; (2.8)
5 0-00
(2.9)
Бо
Где 0ТО— полная влагоемкость породы; В0 — влажность, соответствующая максимальной молекулярной; #к —приведенная высота капиллярного поднятия; Но — скачок давления при полном насыщении. Приведенная высота капиллярного поднятия эквивалентна полному влагосодержанию капиллярной зоны
Со
Нк = $ ёАг. (2.10)
О
Следует отметить, что связь между высотой всасывания и влажностью неоднозначна. Так, при осушении предварительно полностью насыщенной породы связь между влажностью и высотой всасывания характеризуется кривой, где каждому значению соответствует максимально возможное значение влажности. При обратном процессе, когда происходит увлажнение сухой породы, для тех же значений высоты всасывания характерны минимальные значения влажности. Эти две кривые образуют две основные ветви гистерезиса. Смена процессов сушки и увлажнения образует бесконечное множество кривых развертки гистерезиса (петель гистерезиса) в области, ограниченной основными ветвями зависимости (6) (рис. 11).
Коэффициент влагопереноса k также находится в существенной зависимости от влажности. Наиболее общая зависимость k получена теоретическим путем С. Ф. Аверьяновым (1949 г.) и экспериментально подтверждена для многих пород [31]. Эта зависимость связывает коэффициент влагопереноса и влажность степенной функцией
K^kfi4. (2.11)
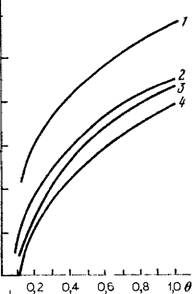
Показатель степени п зависит от характера распределения пор по размерам. Для однородных пород п меняется в пределах от 3 до 4, что хорошо согласуется с теоретическим решением С. Ф. Аверьянова, где п — 3,5. Однако в сущест - т венно неоднородных породах показа - 9 .М/СУТ тель степени п может быть значитель - < но больше. При аппроксимации зависимости £(0) большое значение имеет выбор величины 0о в формуле (2.9). 1б В данном случае влажность 0о характеризует объемное содержание практически неподвижной воды и не всегда соответствует максимальной молекулярной влажности. На рис. 10 пред - 10~3 ставлены зависимости ij)(0), а на рис. 12 зависимости &(0) для некоторых типов пород, слагающих зону аэрации 10 в районах с орошаемым земледелием. В табл. 6 даны примеры констант, 10-« входящих в аппроксимирующие формулы (2.7), (2.8) и (2.11), характер - „6 ные для этих пород. 10
|
10' |
|
Рис. 12. Зависимость коэффициента влагопереноса k от влажности. |
|
/ — супесь легкая; 2 — суглинок средний; S — лёссовидный; 4 — тяжелый |
Следует отметить, что поскольку высота всасывания характеризует равновесное состояние воды в породе, то из-за влияния различных факторов эта величина при одной и той же влажности может быть различной. Соответственно и зависимость - ф (0)
|
Константы, характерные для пород зоны аэрации
|
Для одной и той же породы будет меняться. Повышение минерализации воды приводит к увеличению высоты всасывания, причем растворы различных солей в разной степени влияют на интенсивность удержания воды в породе. В табл. 7 представлены данные о влиянии минерализации растворов NaCl и NaC03 на зависимость влажности от высоты всасывания.
Из представленных данных видно, что влияние раствора Na2CO<, на равновесие влаги в породе значительно существеннее, чем раствора NaCl. В частности, значения влажности завядания, определяемые для воды высотой всасывания порядка 10—15 м (pF = 3— 3,2), для почв, насыщенных растворами NaCl и ЫагСОз, соответ-
|
ТАБЛИЦА 7 Зависимость влажности от высоты всасывания при насыщении породы различными растворами [50]
|
Ственно будут 30 и 40, вместо 25 % для чистой воды.
В деформируемых породах высота всасывания может меняться под влиянием нагрузки. Д. Кроней предложил следующее выражение для высоты всасывания t|j(p) в зависимости от давления воды р и высоты всасывания ненагруженного образца ■ф (0) : (р) = (0) + ар. Коэффициент а определяется по компрессионной кривой согласно
Дж. Филипом (Philip J. R„ 1957 г.)
Где е — коэффициент пористости.
Большое влияние на зависимость k (8) могут оказывать содержащиеся в породе отдельные поры значительных размеров (макропоры). При наличии таких пор даже небольшое уменьшение влажности по сравнению с полным насыщением приводит к резкому уменьшению коэффициента влагопереноса. Для некоторых образцов лёссовидных суглинков Северного Предкавказья уменьшение влажности всего на 0,6 % приводит к уменьшению коэффициента влагопереноса от 0,6 до 10~3 м/сут. Важно отметить, что именно эти макропоры и определяют проницаемость пород в массиве. Коэффициент фильтрации породы с макропорами весьма грубо может быть оценен следующим соотношением:
Ft =10А-г\т, (2.13)
Где гп — радиус поры; т — относительная доля макропор в объеме породы (макропористость). Так, для поры, имеющей радиус 1 мм, & — m • 105 м/сут. Даже если одна такая пора приходится на площадь в 1 м2 (т = 3,14-Ю-6), то коэффициент фильтрации такого образца будет 0,3 м/сут. Экспериментальные исследования подтверждают влияние макропор на проницаемость породы. Проведенная специальная съемка макропор, характерных для лёссовидных суглинков, показала, что в пределах глубин 0—2 м на площади 10 см2 в среднем встречаются 2—3 макропоры. Средний коэффициент фильтрации образцов, специально отбираемых таким образом, чтобы в них не было макропор, составил 0,2 м/сут, а образцов с макропорами — 4 м/сут. При этом наблюдалась и некоторая закономерность в зависимости коэффициента фильтрации от диаметра макропоры (табл. 8).
|
Зависимость коэффициента фильтрации от размера макропоры |
|
Диаметр |
Коэффициент |
|
Макропоры, мм |
Фильтрации k, м/сут |
|
2 |
0,6 |
|
4 |
2 |
|
6 |
4 |
|
8 |
7 |
|
Выражению, предложенному |
Обычно макропоры такого размера встречаются редко и распределены они в пространстве довольно неравномерно. В связи с этим коэффициенты фильтрации, определенные для случайно отобранных
|
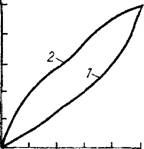
Рис. 13. Распределение красителя в вертикальном срезе почвы. J — после первой фазы промачивання; 2 — после второй фазы промачивания; 3 — неокрашенная область |
Образцов, будут зависеть не только от того, имеются ли в них макропоры или нет, но и от размеров образцов. Даже при больших размерах опробования, например при наливах в кольца, процесс инфильтрации будет в значительной степени определяться движением воды по макропорам. Это наглядно демонстрируется распределением красителя в продольных и поперечных срезах после осуществления кратковременного налива в кольца (рис. 13) для определения фильтрационных свойств покровных суглинков Джизак - ского массива. Различной интенсивностью цвета показано распределение различной краски. Подкрашивание проводилось последовательно разной краской. Как видно, вначале водой заполняются макропоры, а затем происходит боковое впитывание ее в породу. Некоторая, но довольно значительная часть породы оказывается при этом неувлажненной.
В результате исследований дифференциальной проницаемости этих суглинков с помощью гелеобразующего тампонажного алю- мосиликатного раствора, проведенных Н. П. Карпенко и В. И. Сергеевым, установлено, что наибольшее число макропор приурочено к верхней части зоны аэрации, где они занимают 20 % площади. После их тампонажа алюмосиликатным раствором коэффициент фильтрации уменьшается в 7 раз — от 4,3 до 0.6 м/сут. На глубине 0,4 м макропоры занимают 3 % площади, а их исключение уменьшает проницаемость в 1,5 раза — с 0,09 до 0,06% м/сут. Аналогичные результаты получены и для покровных суглинков на террасе р. Волги (Северо-Чагринский массив орошения). В результате тампонажа макропор коэффициент фильтрации этих пород снизился с 0,25 до 0,07 м/сут.
Учитывая эти особенности строения, целесообразно рассматривать породу как многоступенчатую структурную систему. Предельной схемой такой системы является гетерогенно-блоковая схема, для которой характерно наличие макропор. Макропоры здесь являются основными путями, по которым движется вода, а блоки породы между ними характеризуют в основном водоемкость Системы. Макропоры за счет их незначительного объемного содержания оказывают существенное влияние на фильтрацию только при полном насыщении породы. При незначительном уменьшении влажности макропоры осушаются и влагоперенос осуществляется только в блоках. Этим, в частности, можно объяснить существенную разницу в темпах инфильтрации и последующего обезвоживания зоны аэрации. В связи с этим подстановка в зависимость (2.11) коэффициента фильтрации k0 приводит к завышению темпов влагопереноса, особенно при рассмотрении процессов обезвоживания. Расчеты влагопереноса в этом случае следует проводить с учетом только коэффициента фильтрации блоков.
Для характеристики воздухопроницаемости используются те же величины, что и для воды. Проницаемость пород kn [см2], [мкм2] связана с коэффициентом фильтрации соотношением
= (2.14)
Где ті — коэффициент динамической вязкости. 1 мкм2 соответствует коэффициенту фильтрации воды, равному 0,85 м/сут. При расчетах вязкости воздуха можно принимать т] — 1,8 Па-с и у = = 0,0013 г/см3, что соответствует нормальному атмосферному давлению и температуре 20 °С. В Отличие от воды, при движении воздуха в направлении уменьшения давления скорость его фильтрации будет возрастать за счет его расширения. В соответствии с этим будет возрастать и градиент давления. Для изотермически расширяющегося таза можно считать справедливым соотношение
У = UeLAL, (2.15)
Л (Р) dx '
Где V — массовый расход воздуха; у(р) и ті (р) — объемная масса и вязкость, зависящие от давления. Полагая далее, что вязкость
Слабо зависит от давления, а у (р)~у~—, где у — объемная
Рат
Масса воздуха при атмосферном давлении рат, получим иное выражение для массового расхода воздуха
(2-1в)
Соответственно объемный расход воздуха определится в зависимости от давления
Для одномерного стационарного потока воздуха в пористой среде единичный расход v2 на выходе из образца длиной I определится следующим соотношением:
(2-Й)
Где pi и р2 —давление на входе и выходе образца длиной /.
Если давления pi и р2 мало отличаются от атмосферного, иными словами, если избыточное давление находится в пределах 0,1/)ат, то с достаточной точностью можно считать (р«рат), тогда
Kn dp, dff.. р
V ~--- ——т. - k—j-; Я = —
•ц ах ах у
|
ЮО |
|
О 20 40 60 80 S, % |
|
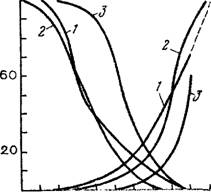
Рис. 14. График относительных фазовых проницаемостей ka Дж. Юхаса (J. Juhasz, 1962 г.). |
|
ТАБЛИЦА 9 Зависимость скорости подъема воздушных пузырьков (J. Juhasz, 1962 г.) от радиуса зерен |
|
Радиус зерна, мм |
Скорость подъема пузырьков, м/сут |
|
0,1 |
88,7 |
|
0,05 |
22,3 |
|
0,02 |
3,58 |
|
0,01 |
0,89 |
|
0,005 |
0,22 |
|
0,002 |
0,03 |
|
По данным |
|
Экспериментальные кривые: 1 — для песка; 2 — для известняка; 3 — для песчаника |
Таким образом, при малых избыточных давлениях закон движения воздуха в пористой среде аналогичен закону Дарси. При малых давлениях наблюдается эффект проскальзывания (эффект Клин - кенберга), приводящий к увеличению расхода газа за счет проскальзывания его молекул вдоль стенок пор. В связи с этим истинная проницаемость среды будет определяться введением поправки
Где — экспериментальная проницаемость газа; Ь — коэффициент Клинкенберга.
|
(2.19) |
Проницаемость породы для воздуха в значительной степени зависит от ее влажности. Максимального значения она достигает в сухой породе и уменьшается до нуля при насыщении, близком к полному. При одновременной миграции воздуха и воды движение каждой фазы рассматривается отдельно. При этом в уравнения движения вводятся значения коэффициентов проницаемости воздуха и влагопереноса в зависимости от влажности породы. График относительных фазовых проницаемостей для песка и песчаника показан на рис. 14. Как видно из графика, в песке движение воздуха прекращается уже при насыщенности, равной 70%. При этом в породе остается защемленный воздух, препятствующий ее дальнейшему увлажнению и снижающий темп влагопереноса. Оставшийся в порах воздух может выйти из породы только в виде
пузырьков. В зависимости от ее дисперсности скорость движения пузырьков воздуха различна. Некоторые значения скорости движения пузырьков воздуха в пористой среде в зависимости от среднего радиуса частиц породы при отсутствии фильтрации представлены в табл. 9.
Эта таблица построена на основании теоретических расчетов, однако приведенные в ней данные убедительно показывают, что в породах с преобладанием пылеватых и глинистых частиц скорость подъема пузырьков воздуха может быть соизмерима со скоростью фильтрации. Последнее может привести к тому, что в течение всего периода фильтрации в породе будет оставаться воздух.
При определении проницаемости пород с помощью воздуха важно учитывать, что при увлажнении может существенно меняться структура породы за счет набухания и заплывания макропор. Кроме того, при увлажнении породы часть воды сорбируется поверхностью частиц, образуя связанную воду и изменяя активную пористость. Эти явления приводят к тому, что воздухопроницаемость оказывается больше водопроницаемости. Причем эта разница особенно ощутима для тонкодисперсных пород. В табл. 10 приводятся средние значения воздухо - и водопроницаемости некоторых пород по данным В. Я. Бурякова [6].
Как видно из таблицы, фильтрация воды вызывает изменения параметров проницаемости в структуре пористого пространства, достигающие нескольких порядков. Использовать воздухопроницаемость пород для характеристики их водопроницаемости иногда вполне возможно, но при этом, как и во всех других случаях, необходимы предварительные лабораторные исследования.
Изменение структуры пород возможно не только при их увлажнении, но и при длительной фильтрации за счет выщелачивания и растворения минерального цемента породы и кольматации пор микрочастицами при высоких скоростях фильтрации.
В обобщающей статье Дж. Митчела и Дж. Юнгера [45J приводятся данные, показывающие, что при фильтрации в глинах наблюдается перераспределение напора вдоль образца (рис. 15).
|
ТАБЛИЦА 10 Сопоставление воздухо - и водопроницаемости
|
|
* В скобках указано число определений. |
|
|
|
20 |
|
Рис. 15, Распределение падения напора ДН вдоль образца. |
|
О 20 40 6 0 80 Щ% |
|
І, CM |
|
Ft, м/сут |
|
Ю |
|
0,0 0,05 0,1 0,2 0,3 |
Изменение коэффициента фильтрации при различной нагрузке
Нагрузка, МПа
0,25-0,7 0,1-0,03 0,08-0,02 0,02-0
О
/ — до начала фильтрации; 2 — спустя 1 ч
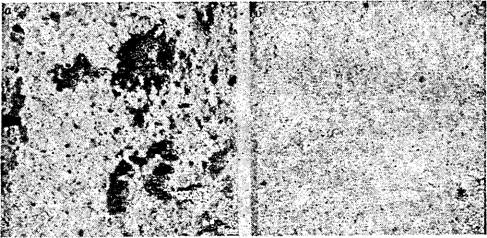
Этот эффект объясняется авторами миграцией частичек по потоку и отложением их на выходе из образца. При этом средний коэффициент фильтрации пород за 1 ч опыта уменьшился с 3,5-10~2 до 3-10~2 м/сут. Процесс изменения структуры, связанный с выщелачиванием цемента, по-видимому, более длительный. Об этом свидетельствуют данные Г. М. Березкиной. На рис. 16 показаны фотографии шлифов (при увеличении в 10 раз) среднеазиатских лёссовидных покровных суглинков до и после опыта, длившегося 20 сут. Как видно, в результате фильтрации структура породы принципиально изменилась. Крупные поры, имеющие размер до 2 мм, полностью исчезли. При этом коэффициент фильтрации образца уменьшился в 20 раз — от 4 до 0,2 м/сут, а его плотность увеличилась с 1,2 до 1,8 г/см3.
|
Рис. 16. Фотографии шлнфов среднеазиатских лёссовидных суглинков. а — до фильтрации; б — после фильтрации |
Хорошо известно, что свойства пород меняются под действием разного рода нагрузок. Так, П. С. Амин-Заде и Т. И. Исмаилов приводят данные, показывающие, что коэффициент фильтрации лёссовых грунтов существенно меняется при приложении нагрузки (табл. 11).
Как видно, увеличение нагрузки на 0,05 МГІа приводит к уменьшению коэффициента фильтрации более чем в 2 раза. Следует отметить, что в этих опытах использовались образцы пород с естественной влажностью, взятых из зоны аэрации. При таком характере изменения коэффициента фильтрации под нагрузкой подъем уровня подземных вод с глубины 10 м к дневной поверхности приведет к уменьшению k на глубине 10 м в 1,5 раза. Таким образом, этот процесс, безусловно, должен учитываться при значительных изменениях давления нагрузки, связанной со строительством, заполнением водохранилищ и при значительном (по крайней мере более 10 м) изменении уровня подземных вод.
Существенную роль в изменении проницаемости играет качественный состав фильтрующейся воды. Многочисленными исследованиями отмечено, что проницаемость дисперсных пород при фильтрации электролитов больше, чем для чистой воды. Увеличение проницаемости более чем в 2,5 раза отмечалось при фильтрации 10%-ного раствораNaCl через монтмориллонитовуюглину [34J. Увеличение k при фильтрации электролитов объясняется сжатием слоев рыхлосвязанной воды вокруг глинистых частиц, вследствие чего увеличивается эффективный диаметр пор. Однако в естественных условиях при невысоких концентрациях раствора изменение композиции пористого пространства в глинистых породах и соответственно изменение их проницаемости происходят главным образом за счет процессов катионного обмена Этот процесс приводит либо к образованию агрегатов, либо к дезагрегации. В качестве примера можно привести результаты эксперимента, проведенного на лёссовидных суглинках, характерных для Явкинской оросительной системы на юге Украины [1]. Образцы отбирались с глубины 2 м. Опыт ставился с целью изучения влияния длительной фильтрации воды с проектным химическим составом на фильтрационные свойства пород. Опыты проводились с нормальной концентрацией раствора и с концентрацией, увеличенной в два раза. Состав фильтрата соответствовал смеси вод рек Ингулец и Днепр (такое смешение предусматривалось проектом). Результаты этого эксперимента приведены в таблицах 12 и 13 и на рис. 17.
На рисунке хорошо видна тенденция увеличения значений коэффициента фильтрации. Последнее связано с изменением состава обменных катионов —замещения Na+ на Са2+ и, как следствие, создание благоприятных условий для образования агрегированных структур. Интересно отметить, что процесс этот достаточно длительный и далеко не всегда может быть выявлен в результате кратковременных полевых экспериментов. В этих же условиях
Результаты эксперимента по фильтрации воды с проектным химическим составом через лёссовидные суглинки
|
№ Опыта |
Емкость поглощения |
Состав обменных катионов, ммоль на 100 г породы |
|||||
|
Са2+ |
Mg2+ |
Na+ |
|||||
|
До опыта |
После опыта |
До опыта |
После опыта |
До опыта |
Тюсле опыта |
||
|
1 2 |
35 38 |
20 18,5 |
27,5 29,5 |
9,4 14,0 |
6,5 8,0 |
5,6 5,5 |
1,0 0,5 |
|
ТАБЛИЦА 13 |
|
Исходное засоление и состав фильтрата
|
,^10 м/сут 10 9 8 7 6
5 4
|
К, Ю"* м/сут |
|
А, |
|
|
|
|
3
-і 1
|
Февраль Март Апрель |
Февраль Март Апрель
Фильтрация раствора NaCl с концентрацией 5 г/л приводит к уменьшению проницаемости практически до нуля.
Более подробно эти процессы изучались применительно к почвенному покрову. В частности, в работе [50] исследовалось влияние различных растворов на коэффициент фильтрации среднего чернозема из горизонта А (табл. 14).
Как видно из таблицы, в данном случае раствор NaCl в рассмотренном диапазоне концентраций практически не влияет на проницаемость почвы. С другой стороны, даже небольшие концентрации раствора ЫагСОз приводят к резкому уменьшению коэффициента фильтрации. Такое различие в эффекте от действия разных растворов может быть объяснено сложным характером ионного обмена в щелочной почве, исходно содержащей СаСОз. Сложность процессов катионного обмена и слабое развитие теории для многокомпонентных смесей вызывают необходимость оценивать возможность изменения коэффициента фильтрации и прогнозировать эти изменения путем постановки прямых экспериментов.
Рассмотренные выше процессы изменения коэффициента фильтрации протекают относительно быстро. Выявление общих тенденций в направлении этих процессов и прогноз проницаемости могут быть сделаны также в результате экспериментальных исследований.
Значительно сложнее давать прогнозы в тех случаях, когда изменение структуры породы происходит медленно, в течение нескольких лет. В первую очередь здесь следует отметить деятельность биологически активной части почвы. По данным Вейсафога, на 1 га среднеевропейской почвы приходится 115 470 кг органического вещества (сухой лес), из них 6388 — живые организмы, 11500 — корни, 97 582 кг — инертная органическая масса. Из живых организмов следует прежде всего отметить почвенных червей (их число доходит до 20 млн. на 1 м2), дождевых червей (на лугах их масса достигает 4 т на 1 га), насекомых, число которых на 1 м2 может превышать 100 тыс. особей. Роль живых организмов в формировании структуры почвы огромна — только червями ежегодно переворашивается до 100 т земли на 1 га. Кусочки растений в результате этой деятельности уменьшаются в размерах до 20—
|
ТАБЛИЦА!4 Влияние состава к концентрации раствора на проницаемость почвы
|
|
Сопоставление коэффициентов фильтрации дренированных и недренированных почв
|
50 мкм. Удельная поверхность растительных осадков увеличивается на 75 % от деятельности червей и на 500 ООО % от деятельности более мелких членистоногих. В этом отношении интересны, например, данные, показывающие практическое прекращение фильтрации при увеличении числа бактерий от І05 до 106 на 1 г породы.
Разрыхление земли корнями растений, появление макропор и каналов на месте перегнивших корней, работа насекомых-земле - роев в совокупности приводят к полной перестройке породы, изменению ее структурных особенностей и проницаемости. Изменение фильтрационных свойств в результате изменения условий жизне - обитания растений под влиянием искусственных мероприятий отмечается в работах Е. Андрияускайте и А. А. Бальчунаса.
Этими исследованиями отмечается, в частности, увеличение коэффициента фильтрации на дренированных минеральных почвах. Некоторые данные из работы А. А. Бальчунаса, подтверждающие это положение, представлены в табл. 15.
Наблюдается также изменение проницаемости в зависимости от расстояния до дрены. Например, для горизонта Ai минеральных почв А. А. Бальчунасом приводятся следующие данные. Коэффициент фильтрации меняется от 0,93—1,66 м/сут в 1 м от дрены до 0,37—0,98 м/сут между дренами; при этом на неосушенных землях он составляет в среднем 0,29—0,48 м/сут.
Совершенно иначе осушение влияет на фильтрационные свойства торфяных почв. Отмечается, что коэффициент фильтрации торфа за 2—4 года уменьшается в 2—3 раза, что связано с его уплотнением.
Динамику изменения коэффициента фильтрации во времени можно продемонстрировать на экспериментальных данных, полученных Номе (Ыёше Lire, 1976 г.) на участке опытного дренажа. Коэффициент фильтрации определялся между дренами в биологически активном слое на глубине 1,3—1,4 м. В табл. 16 представ
лены средние значения коэффициента фильтрации, соответствующие различным периодам времени.
Авторы этих исследований отмечают, что движение воды происходит по избирательным путям, связанным с отмершей корневой системой. Эти макропоры характерны для биологически активного слоя. До работы дренажа в 1969 г. вторичная пористость была слаборазвита. С вводом дренажа улучшилась аэрация почвы, изменились ее тепловой режим и соответственно условия обитания растений и организмов. Уменьшение коэффициента фильтрации в 1973 г. авторы связывают с большим количеством осадков, ухудшением аэрации и соответствующим изменением направления почвенных процессов.
Анализ даже немногочисленных исследований в этой области позволяет считать процесс формирования структуры пород под влиянием почвенных процессов достаточно медленным. В связи с этим прогнозы изменения фильтрационных свойств могут даваться только на основании опыта эксплуатации аналогичных систем.
Емкость водоносных пластов. Изменения емкости водоносных пластов при нестационарном режиме фильтрации происходят двумя принципиально различными путями: а) в связи с гравитационным насыщением или осушением пород, происходящим в безнапорном потоке при подъеме или опускании свободной поверхности (гравитационная емкость); б) за счет расширения или сжатия пород и воды в процессе упругого режима фильтрации (упругая емкость). Изменение гравитационной емкости пласта характеризуется коэффициентом гравитационной водоемкости р,0, который представляет собой изменение количества воды в порах при гравитационном осушении или насыщении, отнесенное к объему грунта; при опускании свободной поверхности цо соответствует коэффициенту водоотдачи а при повышении свободной поверхности — коэффициенту насыщения Для величин fxB и jxH можно записать следующие формулы: jxB = Qm — Bo — бет, = 0m — 0е, где бт — влажность грунта в насыщенном водой состоянии (под свободной поверхностью); 0СТ — влажность стыковой воды (в углах пор); 0О — объемное содержание связанной воды; 0е — влажность грунта в воздушно-сухом состоянии (над свободной поверхностью). Для песков, супесей и суглинков значения коэффициентов р, в И р, н обычно колеблются в пределах 0,05—0,25.
|
Изменение коэффициента фильтрации во времени |
|
Время определения, год |
К, м/сут |
|
1969 |
0,31 |
|
1972 |
1,15 |
|
1973 |
0,75 |
|
1974 |
1,70 |
|
1975 |
1,75 |
Наличие в породах макропор и трещин обусловливает специфический режим насыщения и осушения пород, для которого характерны два этапа, связанные с изменением водосодержания макропор и агрегатов (блоков). В таких гетерогенных породах макро - поры и трещины являются основными водопроводящими путями.
Несмотря на то что их объемное содержание в породе очень мало (до 5 % от общего объема породы), именно они и определяют проницаемость пород в массиве. Блоки или агрегаты породы характеризуются значительно меньшей проницаемостью, но при этом в основном определяют ее водоемкость. Первый этап осушения или насыщения пород связан с изменением водосодержания трещин и макропор. Для этого этапа характерны низкие значения коэффициента р,0 — порядка 0,05. На втором этапе происходит насыщение агрегатов.
Для анализа процесса насыщения агрегата рассмотрим следующую простую схему. Агрегат геометрической формы, которая может быть произвольной, в какой-то момент времени оказывается окруженным со всех сторон водой. На поверхности агрегата граничное условие г|) — 0 сохраняется постоянным до тех пор, пока приток по макрокапиллярам достаточно интенсивен, чтобы обеспечить постоянное увлажнение поверхности агрегата. Динамику насыщения агрегата в упрощенной постановке можно представить в следующем виде:
V("О
Где V— объем агрегата; ш — его поверхность; 0 —среднее значение объемной влажности; к — коэффициент влагопереноса; чр — средняя высота всасывания; / — характерная длина, определяющая средний путь влаги. Далее, считая связь между влажностью и высотой всасывания линейной, а коэффициент влагопереноса усредненным по влажности, получим следующее решение уравнения (2.21):
§ = 1 _ Т = (2.22)
«0 "к
Сопоставление приближенной формулы (2.22) с решением на электроинтеграторе, где этот процесс рассматривался в более сложной постановке [27], показало возможность использования ее для практических расчетов. Анализ этой зависимости в свою очередь показывает, что практическое насыщение агрегата происходит по истечении времени t, в 3 раза превышающего характерное время запаздывания т (/>3т). При этом, учитывая сложность определения входящих в т параметров, целесообразно рассматривать характерное время запаздывания как самостоятельный параметр и назвать его временем влагообмена. Для реальных пород т колеблется в пределах от 0,01 до 2,0 сут. Таким образом, интенсивность впитывания зависит от влагосодержания блока и определяется следующим соотношением:
_L (і _ё). (2.23)
Малые значения времени влагообмена характерны для агрегированных пород с размером агрегатов до 1 см. Для пород, пронизан
ных макрокапиллярами, происхождение которых связано с деятельностью землероев, значения т могут достигать 1 сут.
При подъеме свободной поверхности может происходить защемление воздуха, приводящее к уменьшению потенциальной во- доемкости породы. Объем защемленного воздуха может быть соизмерим с водоемкостью и в некоторых случаях превышать половину ее величины. Прекрасными ловушками воздуха являются агрегированные породы. При подъеме уровня вода движется по трещинам и макропорам, а блоки породы остаются практически сухими. Впитывание воды в блоки происходит медленно и может прекращаться при наступлении равновесия между давлением замкнутого воздуха и капиллярными силами.
Дегазация породы осуществляется вследствие растворения воздуха в воде и удаления его по крупным порам в виде пузырьков. Несмотря на существенное влияние воздуха, насыщение агрегированных пород происходит значительно быстрее, чем их осушение. При спаде уровня сначала осушаются макропоры и трещины, а блоки и агрегаты породы остаются насыщенными. Связь между агрегатами может ухудшаться настолько, что их осушение гравитационным путем в некоторых случаях становится невозможным.
Рассмотренная простая схема, учитывающая защемление воздуха при насыщении агрегатов, показывает, что в этом случае темп впитывания значительно ниже, чем при предположении о возможности беспрепятственного удаления воздуха. Изменение влагосо - держания агрегата без учета растворения воздуха приводит к следующему уравнению:
DQ ____
Dt х і - 6
Где ро — давление воздуха, при котором началось насыщение. Сопоставление (2.23) с (2.24) показывает, что в суглинистых породах, для которых p0f2HK^l, скорость насыщения блока (при 0 = = 0,3) в случае защемления воздуха будет почти в три раза
Меньше. При этом равновесное содержание влаги ^когда =
Будет соответствовать значению 8 = 0,4, иными словами, коэффициент недостатка насыщения может быть более чем в два раза меньшим коэффициента водоемкости ц0. Упругая емкость водоносных пластов проявляется при изменениях давления в породе и воде и характеризуется коэффициентом упругоемкости т}, который представляет собой изменение объема воды в единичном объеме потока при единичном изменении напора.
В табл. 17 приведены некоторые характерные значения упругоемкости пород [20J.
В плановых потоках удобнее пользоваться коэффициентом упругой емкости пласта р,*, который представляет собой изменение объема воды в единичном элементе пласта (единичной площади
|
П. м~1 |
ТАБЛИЦА 17 Характерные значения упругоемкости пород
Породы
Скальные
Песчаные и гравелистые Супесчаные и глинистые
|
(0,02-1,7) • 10-5 (0,5-5) • 10-* Ю-З-Ю-4 10-5-10-6 |
Глубокие водоносные горизонты
В плане) при единичном изменении напора; в однородном пласте мощностью т имеем р,* == ц*т, а в слоистом пласте, состоящем из п слоев с мощностью г'-го слоя ті и коэффициентом упругоемкости Т];, ПОЛуЧИМ
П
£ пХ-