ГИДРО­ГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ

ОСНОВЫ ФИЗИКО-ХИМИЧЕСКОЙ ГИДРОДИНАМИКИ СОЛЕОБМЕНА И СОЛЕПЕРЕНОСА

При изучении физико-химического характера процессов рассо­ления следует, разумеется, учитывать представления о токсичности различных солей. По Н. И. Базилевич и Е. И. Панковой, за кри­терий засоления принимается «суммарный эффект» токсичных ионов, выраженный в эквивалентах по С1, исходя из следующих соотношений: 1С1 = 0,1СОз — 2,5НС03 = 5S04. По величине «сум­марного эффекта» (будем обозначать его Сся) почвы разделяются по степени засоления на: незасоленные (од = 0,3 ммоль), слабо - засоленные (Сс1= 0,3—1 ммоль), среднезасоленные (cci=l— 3 ммоль) и очень сильнозасоленные (ссі = 7 ммоль).

При обосновании физико-химических моделей процессов соле - обмена водный раствор обычно считается однокомпонентным, од­нозначно характеризующимся концентрацией солей «с». Рассматри­вая такую модель, как первое приближение, можно в качестве «с» принимать величину «суммарного эффекта» са или концентрацию преобладающих солей. Вместе с тем при сложном солевом составе водного раствора отдельные компоненты характеризуются совер­шенно различными условиями солевого обмена между жидкой и твердой фазами и такая модель уже может быть неудовлетвори­тельной. Например, при сульфатно-хлоридном или хлоридно-суль - фатном засолении сульфаты переходят в водный раствор значи­тельно труднее, чем хлориды, гораздо дольше оставаясь при промывках в твердой фазе. В таких случаях можно проводить рас­четы солевого обмена и переноса для каждого компонента в от­дельности, без учета их взаимовлияния. Однако такой подход еще требует экспериментального обоснования, которое до сих пор не осуществлялось.

Для растворения солей, находящихся в твердой фазе, Н. Н. Ве - ригин предлагает [10] уравнение кинетики вида

(5.1)

Где jVt — содержание солей в твердой фазе в единице объема грунта; сп — концентрация насыщения; у— коэффициент скорости растворения; k — параметр, зависящий от характера распределе­ния солей в грунте (& = 0 при пленочном засолении, & = 0,5 при дисперсном засолении). Применительно к этому типу уравнения для растворения гипса, дисперсно распределенного в песчано-гли - нистых грунтах, А. Е. Орадовской получены значения у = 10— 100 сут-1.

Уравнения физико-химического обмена должны рассматри­ваться далее совместно с уравнением переноса солей, получаемым из условия неразрывности солевого потока. Запишем такое урав­нение для одномерного гомогенного потока, движущегося в направ­лении I со скоростью фильтрации v, учитывая конвективный пере­нос и микродисперсию, обусловливаемую молекулярной диффузией и гидродисперсией

Дс d(cv) , дМг дч

+ + —дГ__ О - gl2 . (5.2)

Здесь D — коэффициент микродисперсии, который складывается из коэффициента молекулярной диффузии DM и коэффициента гидродисперсии Dr == 8jV, где параметр гидродисперсии бг зависит от структуры среды. Для песчаных и глинистых пород характерное значение DM = 10~5 м2/сут, а параметр гидродисперсии наиболее обоснован для мелкозернистых песков, имеющих ориентировочно бг= 1 мм [10, 38].

Дальнейшее рассмотрение модели солепереноса будем прово­дить для хорошо растворимых солей (главным образом хлоридов), пренебрегая кинетикой их растворения.

Важнейшим геологическим фактором солепереноса является фильтрационная гетерогенность среды, обусловлен­ная особенностями литологического строения пород, а также нару­шениями, вызываемыми деятельностью растений и землероев.

/ О,

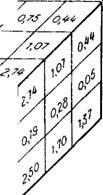
Рис. 59. Распределение коэф­фициентов фильтрации (м/сут) по блокам монолита супесчано - суглинистых пород. По мате­риалам Е. К. Широковой и Ш. А. Караулова

Характерный пример структуры филь­трационного строения супесчано-суглини - стых отложений, обусловленного их лито ло­гической неоднородностью, представляют данные определения коэффициента фильтра­ции в отдельных блоках монолита, вырезан­ного с поверхности земли в периферийной части конуса выноса (район Голодной степи). Монолит имел форму куба с разме­ром сторон 1 м и разрезался на 27 кубиче­ских блоков размером ~0,3 м (рис. 59). Для каждого из блоков по данным про­дувки воздухом определялся коэффициент проницаемости (Ш. А. Караулова, Е. И. Ши­рокова), который пересчитывался в ко­эффициент фильтрации по воде. Значе­ния коэффициентов фильтрации приведены на рис. 59 для видимых на такой про­екции блоках, а полностью они приведены в табл. 39.

Как видно, в данном случае в пределах каждого горизонтального слоя по глубине значения проницаемости меняются в не­сколько раз, причем не выявляются какие - либо закономерности изменчивости этих значений по площади; более четкой является

Наиболее простой и употребительной расчетной моделью, не­посредственно учитывающей фактор гетерогенного строения, яв­ляется квазиоднородная гетерогенно-блоковая среда (среда с двойной емкостью), в которой порода принимается со­стоящей из равномерно распределенных слабопроницаемых бло­ков, прорезаемых проницаемыми каналами (прослоями, трещи­нами), причем в проницаемых каналах перенос осуществляется только конвективным путем, а в слабопроницаемых блоках— только диффузионным путем. Существующие варианты этой мо­дели различаются по характеру развития диффузионных процес­сов в блоках. Наиболее простым и употребительным вариантом является схема «сосредоточенной емкости» блоков елоисто-столб-

Чатого строения [38J, в которой обмен между проницаемыми кана­лами и слабопроницаемыми блоками происходит только диффузи­онным путем, причем диффузионный поток в пределах блока осредняется.

Для решения мелиоративных задач солепереноса такого рода модель была впервые предложена В. Гарднером и Р. Бруксом [31], которые выделяли «мобильные» (двигающиеся вместе с водой) и «иммобильные» (отстающие от потока) соли. К такой же модели относится представление пористой среды в виде системы проход­ных и застойных («тупиковых») пор [31].

Анализ реального фильтрационного строения горных пород по­казывает, что нередко проницаемость блоков и каналов разли­чается не столь резко, чтобы можно было пренебрегать конвектив­ным переносом в блоках. Для учета этого фактора можно исходить из представления о мозаичной схеме строения породы (рис. 60), в которой учитывается, что в блоках идет фильтрация со средней

Yv /V

Скоростью k*v, где k* — относительная проницаемость блока, а ■& — средняя скорость фильтрации.

Исходя из такой схемы строения породы, рассмотрим солевой баланс блока объемом V&, площадью поверхности <йб и средней площадью горизонтального сечения сог. Обозначая концентрацию солей в каналах через с, а в блоке через с*, запишем выражения для расхода поступления солей в блок диффузионным путем

£ __

Од—DM®6 —j-—*

Где /б — расчетное расстояние от поверхности до центра блока; DM — коэффициент молекулярной диффузии блока. Расход конвек­тивного поступления солей в блок при скорости фильтрации %*v определяется выражением

QK = k*var (с-с*). (5.4)

Составим далее уравнение ба­ланса солей в блоке

Дс*

Q* + QK=nV6

Где п — активная или эффектив­ная пористость породы. Совмест­ное решение этих уравнений дает дифференциальное уравнение внутреннего солеобмена

-а (с — с*),

Рис. 60. Направления переноса в гетерогенно-блоковой среде мо­заичного строения.

1 — направлення конвективного пере­носа в каналах, 2—3 — диффузионного (2) и конвективного (35 переноса в блоках

Где а — коэффициент солеобмена, составляющие которого ад и ак отражают действие диффузионного и конвективного переноса в блоках, причем

Ад=/?м1^б-) ак = k* • (5.6а)

В такой модели величина коэффициента массообмена оказы­вается линейно зависящей от скорости фильтрации и при

И ©б~©г~/2б можно представить структуру коэффициента массо­обмена в следующей форме:

Г) в*

А=ад + Хі>, X------ (5.7)

Для оценки относительной значимости конвективного и диффу­зионного переноса в блоке рассмотрим соотношение диффузионной и конвективной составляющей коэффициента массообмена, прини­мая, что блоки, имеют кубическую форму с размером стороны 2/б; тогда ©б = 24/2, Шг __ и

Ак k*v шг/б

—------- —_—• (5.8)

АД им (£»б Di^vi

Например, при характерных для зоны аэрации значениях h —

/■ч/

= 0,3 м, DM = 10~5 м2/сут, v = 0,1 м/сут, k* = 0,1 получим из (5.8)

«К 0,1-0,1.0,3 ол

~—їо^-зГ--- = 20, т. е. в этом случае диффузионныи пере­нос в блоке имеет пренебрежимо малое значение и внутренний массообмен идет главным образом конвективным путем, так что можно считать a~v. Этот пример показывает, что внутренний конвективный перенос в блоках может играть существенную роль в формировании процессов солепереноса.

В дополнение к уравнению внутреннего солеобмена следует записать общее уравнение солепереноса в проницаемых каналах и блоках. Для его вывода составим баланс солей в представитель­ном элементе потока объемом V, включающем в себя блок объемом Ve и относящиеся к нему каналы объемом FK - Пренебрегая диспер­сией солей в каналах, получим следующее балансовое уравнение:

—AQc=n (rK + Гб •), (5.9)

Где AQC — изменение расхода солепереноса в пределах рассматри­ваемого элемента. Выражение для этого расхода

Qc=<3KoKc-f co6&*vc*, (5.9 а)

Где ©к — площадь поперечного сечения каналов; vK — скорость фильтрации в каналах.

Дальнейший вывод дадим для одномерного потока в направле­нии I, характеризующегося средней скоростью фильтрации v. Обо­значая через х относительное содержание каналов и считая его одинаковым по объему и по площади поперечного сечения, имеем

V — XVK + (1 — к) k*V, ©к = Кй>, ©6= (1 — к) и, (5.10)

Где а) — площадь поперечного сечения рассматриваемого элемента. Тогда выражение (5.9а) приводится к виду

Qc = <ai> [е + £* (1 — х) (с* — с)]. (5.11)

Подставляя это выражение в балансовое уравнение (5.9) и имея

6Q

В виду, что —~АI и А1 = V/w, получим

Пк + й (1 — к) + v [с + Л*(1-к) (с* — с)]=0. (5.12)

При относительно малой проницаемости блоков можно пренебречь членом k*(l—х)(с* — с) и тогда уравнение (5.12) примет вид

«к (1 - к) (5ЛЗ>

Широкое использование в качестве исходной теоретической модели получила схема макродисперсии, в которой обычно прини­мается [1, 10, 19], что для хорошо растворимых солей все процессы внутреннего солеобмена учитываются введением обобщенного ко­эффициента макродисперсии D*, определяемого опытным путем. В этом случае дифференциальное уравнение для одномерного по­тока получается из (5.2) с заменой D на D* и исключением чле­нов, учитывающих солеобмен между жидкой и твердой фазами

Й JL л - п* — (5 14)

Dt + dl — ^ а/2 • <оЛ4>

Капитальное приложение такой теоретической модели к реше­нию мелиоративных вопросов с разработкой методики решения за­дач рассоления мелиорируемых земель было осуществлено С. Ф. Аверьяновым [1], а в последующем эти разработки были раз­виты для различных расчетных схем [19, 31]. На основе этой мо­дели были проанализированы натурные материалы солепереноса на орошаемых территориях, причем оказалось, что расчетные ве­личины параметра D* имеют значения порядка Ю-2 м2/сут, что су­щественно выше значений коэффициентов молекулярной и фильт­рационной диффузии. Это обстоятельство подтверждает, в частно­сти, предположение, что в природных условиях гетерогенность среды оказывает существенное влияние на характер солепереноса. Модель макродисперсии имеет определенное теоретическое обосно­вание на основе представлений о стохастическом представлении переноса в гетерогенной среде, однако правомерность применения этой модели к реальным породам требует доказательств, которых в существующих материалах не имеется.