ГИДРОГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ
Насыщение и осушение зоны аэрации при колебаниях уровня
При изменении уровня подземных вод происходит сложный процесс переформирования режима влагопереноса. При снижении или повышении уровня с постоянной скоростью в зоне аэрации при
Условии ее достаточной мощности формируется определенный профиль влажности, соответствующий скорости влагопереноса. При снижении уровня профиль влажности будет вытягиваться, стремясь к равновесному состоянию, обеспечивающему постоянный расход воды. При подъеме уровня равновесное состояние характеризуется сжатым профилем влажности. Для формирования равновесного профиля даже при равномернохм изменении уровня требуется длительное время. В связи с этим коэффициент водоотдачи или недостатка насыщения, определяемый экспериментальным путем, в начале процесса значительно меньше коэффициента водоем - кости породы. Со временем он возрастает, стремясь к постоянной величине.
Анализ изменения коэффициента водоотдачи при изменении уровня позволяет выделять текущий коэффициент водоотдачи (2.31) и предельный коэффициент водоотдачи, определяемый суммарным количеством воды, прошедшей через свободную поверхность, отнесенным к изменению уровня
А + дй
ST S (2-82)
H
Из экспериментальных данных Н. 3. Моркоса и Б. М. Живовой следует, что коэффициент водоотдачи существенно зависит от скорости снижения уровня. Для анализа этого процесса представим капиллярную зону в виде набора капилляров. Для каждого капилляра характерны высота капиллярного поднятия г^ и коэффициент фильтрации ki, определяемые в зависимости от функций ф (6) и k{%). Сечение каждого капилляра определяет его элементарную емкость А8 (рис. 24). Динамика изменения высоты воды h в каждом капилляре при постоянной скорости уровня воды и определяется соотношением
Dli 1 1, (2.83)
Dx0 h + ито
Hi U Ы
Где h = -~ ; и — -; т0
Фі ki
Правомерность такой модели доказывается сопоставлением опытных данных и расчетом (рис. 25).
Соответственно коэффициенты водоотдачи р.,- и предельной водоотдачи Щі для каждого капилляра можно найти по формулам:
А9 dh /0
И
|
• де. |
|
Т |
|
"т0 |
(2.85)
|
|
|
Z. CM 120 Too 80 |
|
Рис. 24. Графики определения т{>< (а) н (о) для элементарного объема Д0 |
Рис. 25. Сопоставление данных по динамике влажности при осушенни колонны песка, полученных расчетом на: 1 — 5; 2—10; 3 — 20; 4 — 45 мин, с опытными данными работы [49] (5)
|
(2.86) |
Полные значения водоотдачи р, и \xk определятся далее суммированием
Yi м-t и М-Л = llki >
T=i
Где п — количество капилляров. Заметим, что A0n = 0т— 0О соответствует водоемкости породы ро-
|
(2.87) (2.88) |
Расчет по формулам (2.84), (2.85) показывает, что для различных значений й динамика рг- и может быть описана экспоненциальной функцией
Щ = Л0 1-ехр^-0,16^ № = AOj^l - exp ^—0,08
Учитывая, что закон изменения элементарной водоотдачи одинаков для различных скоростей снижения уровня, коэффициент водоотдачи можно определить либо по формулам (2.86), либо интегрированием непрерывных функций 1
Fexpf-0,16МЩ <й1
Для анализа зависимости водоотдачи от времени проведем численный расчет по формуле (2.89) при следующих параметрах:
|
1 |
|
(2.89) |
|
Ц = Но |
K = ko&, ф = 2НК (1 — 0); п -4. Результаты расчета представлены в табл. 23.
|
Зависимость ji от t
|
Как видно, процесс изменения водоотдачи во времени весьма и весьма длительный, а его динамика определяется безразмерным
2
Г М „
Временем запаздывания ^ = — ---. Время, начиная с которого
ІІПц
Коэффициент водоотдачи определяется с точностью 20 %, можно определить из соотношения
|
?>6,3. 10*-^-. (2,90) |
Нки k2
Так, для песков с коэффициентом фильтрации 10 м/сут и Нк — = 0,1 м при скорости снижения уровня 0,01 м/сут для оценки водоотдачи с точностью 20 % требуется время порядка 0,6 сут. При тех же условиях для супесей с k = 1 м/сут и Як — 1 м этот период составляет 600 сут. Следует отметить, что полученные оценки справедливы для принятых зависимостей параметров влагопереноса от влажности. Для других зависимостей пороговое время, начиная с которого водоотдача становится практически постоянной, будет иным. При усредненной по влажности высоте капиллярного поднятия Як и линейной зависимости коэффициента влагопереноса от влажности пороговое время определится следующим соотношением:
(2.91)
K0
При этом точность определения водоотдачи составит 20%. По-видимому, именно указанными выше особенностями объясняются низкие значения коэффициента водоотдачи для тяжелых и средних пород, полученные по данным режимных наблюдений и откачек. Обычно для суглинков ^х = 0,01—0,05, для супесей р = 0,05—0,1, что значительно меньше водоемкости этих пород — ро=0,2—0,25. Особенно сложно протекают процессы осушения и насыщения зоны аэрации при изменении темпа подъема уровня и смены направления его движения на обратное. В этом отношении весьма показательным представляются результаты опыта, проведенного Юнгсом (Youngs Е. G., 1969 г.). Эксперимент состоял в периодическом дождевании лизиметра с песком, с фиксированием расхода
А
|
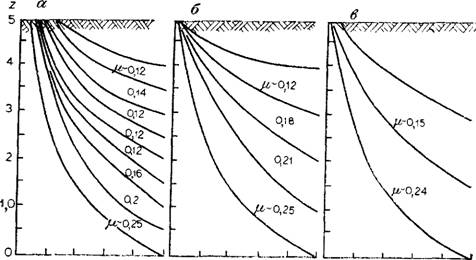
Рис. 27. Характер изменения влажности при различных скоростях поднятия уровня. А — а—О,5; б — «= 1; s — а= 1,5 м/мес. Цифры у кривых — значения коэффициента насыщения
0,25 0,3 0,35 0,4 0,45 0,25 0,3 0,35 0,4 0,45 0,25 0,3 0,35 04 в |
Qg стекающей из поддона воды. Юнге исследовал динамику коэффициентов насыщения и водоотдачи, которые удовлетворяли бы обычно используемому балансовому соотношению
Dh
Qg - qw = - Ц. (2.92)
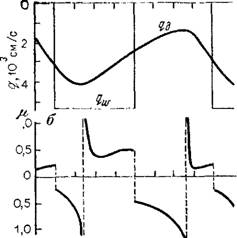
Где qw — расход воды, поступающей на поверхность лизиметра. На рис. 26 представлены графики изменения величин qg, qw, р, определенных по формуле (2.92). Положительные значения соответствуют водоотдаче, отрицательные—насыщению. Как видно из рисунка, значения коэффициента водоотдачи меняются во времени в широких пределах и на некоторых этапах достигают неправдоподобно больших величин.
|
О 20 40 60 і, мин |
|
Рис. 26. Динамика водоотдачи по данным Юнгса (Е. G. Yongs, 1969 г.). А — изучение интенсивности дождевания и оттока из лизиметра; б — динамика коэффициента водоотдачи |
При длительных и монотонных процессах, когда темп изменения уровня остается постоянным, коэффициенты водоотдачи или
насыщения можно считать равными соответствующим коэффициентам емкости. К таким процессам можно отнести: подъем уровня при орошении, если исходная его глубина была достаточно большой; подпор прибрежных территорий в районе каналов и водохранилищ; длительное водопонижение в связи с эксплуатацией подземных вод.
Как следует из формулы (2.31), коэффициенты водоотдачи или насыщения зависят от положения свободной поверхности подземных вод относительно поверхности земли. Особенно эта зависимость начинает проявляться при глубине залегания уровня порядка 3Як. Моделирование подъема уровня в суглинках (0т = 0,45, Вэ = = 0,2, k = 2 -10~2 м/сут, #к = 1 м) подтвердило это положение (рис. 27). При подъеме уровня со скоростью 0,5; 1 и 1,5 м/мес коэффициент насыщения зависел не столько от скорости подъема уровня, сколько от положения его относительно дневной поверхности. При глубине уровня 4 м, и = 0,25, при глубине 3 м р, = 0,18; при глубине 1,5 м р —0,12. Зависимость коэффициентов насыщения и водоотдачи от глубины уровня подземных вод рассмотрена в ряде работ и наиболее полно обобщена С. Ф. Аверьяновым [14]. Им были получены зависимости для текущего и предельного коэффициентов водоотдачи из предпосылки неизменности профиля влажности над уровнем подземных вод. Следует отметить, что на эту зависимость влияют не только характер связи между высотой всасывания и влажностью, но и процессы, которые происходят в зоне аэрации. В частности, при поступлении в нее воды или при испарении зависимость коэффициентов насыщения или водоотдачи будет различна.
|
|
Эти особенности можно учесть, считая в первохМ приближении зависимость влажности от высоты всасывания линейной величиной, а коэффициент влагопереноса — постоянным и равным коэффициенту фильтрации. Для этой простой модели коэффициенты водоотдачи или насыщения определятся по формуле
(2.93)
При инфильтрации / следует принимать отрицательным, а при испарении — положительным. Причем в первом случае формула
Справедлива при - г—^ 1, а во втором —при -—<2Нк— 1. Соот-
«0 Ко
|
(2.94) |
Ветственно коэффициент предельной водоотдачи
Цк = 0,5р.0.
Зависимость (2.93) может применяться при z<2HK.
Близкая к линейной зависимость между водоотдачей и глубиной залегания уровня подтверждается прямолинейностью графика (рис. 28), на осях которого отложены свободный объем зоны аэрации V = Рк2 И 22.
Совершенно иначе протекает процесс осушения и насыщения пород в среде с гетерогенно-блоковым строением. Насыщение по
род происходит очень быстро, по - скольку вода при этом может пере - 08 - двигаться по макропорам и трещинам. Причем, поскольку их доля в общем объеме породы очень мала, процесс заполнения трещин и макропор происходит очень быстро. Полное насыщение происходит с запаздыванием, определяемым временем влагообмена, однако период этот очень непродолжителен и редко превышает 1 сут. При снижении уровня в первую очередь происходит осушение макропор и трещин, которые определяют очень низкие значения водоотдачи, не превышающие обычно 5 %. Затем начинается процесс осушения блоков и агрегатов породы, длительность которого может превышать 10 сут. Опыт определения водоотдачи при откачках в двухслойной среде, где покровные отложения представлены средними и тяжелыми породами, показывает, что даже при весьма длительных откачках коэффициент водоотдачи не превышает 5%. Анализ этого процесса, данный в работе [21], показывает, что фаза полного гравитационного режима для средних суглинков наступает только через 100 сут от начала опыта. Из этого анализа, в частности, следует, что постановка откачек для определения водоотдачи в тяжелых породах лишена практического смысла.