ГИДРОГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ
Методы расчета влагопереноса в зоне аэрации
Расчеты влагопереноса в зоне аэрации базируются на решении уравнения баланса влаги в зоне аэрации. Сложность решения уравнения влагопереноса определяется его нелинейностью. Имеющиеся предложения по аналитическому решению уравнения (2.32) касаются простых схем влагопереноса и связаны, как правило, с большим объемом вычислений. Не упрощает ситуации в этой области и линеаризация уравнения (2.32). Предложения по способам линеаризации этих уравнений сводятся к осреднению тем или иным образом параметров переноса. При этом уравнение (2.32) приводится к виду
П д2д л. ь 30 - т (О <к*
|
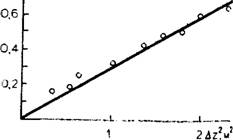
Рис. 28. Зависимость объема осушения зоны аэрации V от глубины уровня Дг2. По данным В. Виссерз (W. С. Visser, 1969 г.) |
+ к = —. (2.95)
П. Я - Полубариновой-Кочиной был предложен способ линеаризации, заключающийся в замене кривых D (0) и k (0) отрезками касательных, проведенных либо в левой или правой конечных точках, либо в средней точке интервала изменения влажности. В дальнейшем наибольшее распространение получил способ осреднения параметров в средней точке, рассмотренный, в частности, Ю. Н. Никольским. При изменении влажности в пределах от 0И до 0В принимаются параметры:
І ®в
Do = -7Г---П - \ D (Є) dB (2.96)
Ив — "н J
Єн
И
Ев
\ k (0) (2.97)
Н
И. А. Фавзи и В. М. Шестаковым предложен способ осреднения параметров влагопереноса во времени. При этом D0 и k0 принимаются в зависимости от того, при какой влажности интенсивность ее изменения оказывается наибольшей. При рассмотрении всего периода времени эти авторы рекомендуют принимать параметры, средневзвешенные по времени. Приведенное ими сопоставление двух способов линеаризации показало, что наилучшие результаты дает осреднение параметров в соответствии с влажностью периода максимальной интенсивности процесса. Следует отметить, что последний способ требует априорного знания течения процесса, что не всегда возможно. С помощью аналитических решений линеаризованного уравнения (2.32) получают приближенные результаты,, анализ которых позволяет рассмотреть качественную картину движения воды в зоне аэрации только для сравнительно простых процессов.
Сложность дифференциального уравнения влагопереноса предопределяет необходимость использования в основном численных методов расчета с применением электронно-вычислительных цифровых машин (ЭЦВМ), аналоговых вычислительных машин (АВМ) и электроинтеграторов (ЭИ).
Применение численных методов, реализуемых на ЭЦВМ для решения уравнения влагопереноса, имеет достаточно большую историю. К одним из первых работ в этом направлении относится работа Лиакопулоса и Рубина (G. Liakopulos, 1966 г., J. Rubin, 1968 г.).
Большие возможности мощных вычислительных машин позволяют осуществлять достаточно сложные расчеты влагопереноса даже для пространственных задач. Для решения задач мелиоративной гидрогеологии разработаны аэгоритмы и программы, описания которых можно найти в работах [2, 16].
Несмотря на явную целесообразность применения ЭЦВМ для расчетов влагопереноса, пока эти методы не получили должного
распространения, что связано прежде всего с необходимостью использования довольно мощных ЭЦВМ с большим объемом памяти. Учитывая это, представляется целесообразным рассмотреть и другие возможности решения уравнения влагопереноса с использованием промышленных аналоговых машин, которые в некоторых случаях даже на данном этапе могут успешно конкурировать с ЭЦВМ. Решить уравнения (2.33) на электроинтеграторе можно по
Схеме Либмана [271 с заданием члена —— как истока. Для этого
Oz
Представим уравнение (2.33) в виде
Di + l+Di ( б?-и-в? ) Dj+Di. і ( в| — в/_і )
2 \ Az J 2 V Az J
Ц-ё'Г"
+ £ =------------ At-------- Лг' (2.98)
Где
Или
0/ + 1 -6І, ,
+ ------------------ • (2.100)
Фі + 1,і Фі, і-1 Фі
Где
^ 2Дг ^ 2Дг Д* .. 4Л1Ч
Ф,+1'г= Dt + l+DP Фг'г-1= D7+WT' (2Л01>
Электрическим аналогом этого уравнения является уравнение, описывающее баланс токов в цепи
Переход от влажности, фильтрационных сопротивлений и расходов к соответствующим им потенциалам, омическим сопротивлениям и токам осуществляется с помощью переходных коэффициентов
В«в1Г' = (2Л03)
Которые задаются в зависимости от конструктивных особенностей моделирующего устройства. В том случае, когда моделирующее устройство не имеет делителя токов, гравитационная составляющая может учитываться на каждый шаг по времени путем задания на концах временных сопротивлений потенциала, пропорционального
|
Kj + i — kj _ і 2 Дг |
|
В* |
|
"і- |
At. (2.104)
Особенностью моделирования уравнения (2,98) является то, что сопротивления модели необходимо менять при каждом новом
Шаге времени сообразно изменениям коэффициента влагопровод - ности. При этом в принципе необходимо производить подбор сопротивлений таким образом, чтобы средние значения коэффициентов фильтрации соответствовали средним значениям влажности в центрах блоков. Однако решение задачи в такой постановке значительно усложняет и удлиняет процесс моделирования. В связи с этим корректировку сопротивлений удобнее проводить на каждый шаг времени в соответствии с данными предыдущего шага. Исследования И. А. Фавзи и В. М. Шестакова показали, что итерации при задании величины k и D необходимы только для двух первых шагов времени. Дальнейшее решение задачи можно проводить, задавая значения этих параметров в зависимости от влажности на начало интервала At
Di+t'+Di-" І4-
|
"дГ |
— ^ д2 J 2 V Л2 J
+ ------- . (2.105)
Но даже при использовании этого метода процесс решения задачи остается чрезвычайно трудоемким.
Другой путь решения этого уравнения представляется перспективным для практического использования на обычных электроинтеграторах. Он основан на ряде преобразований уравнения влагопереноса, представленного в терминах давления при положительном направлении (вверх) оси z
Дг('
Введем переменной т) = J уравнение (2.106) можно при
Вести к виду
Как видно, в такой постановке отпадает необходимость в изменении сопротивлений, моделирующих вторую производную. Корректировать в данном случае нужно только токи и временные сопротивления. В некоторых случаях, когда зависимость коэффициента влагопереноса и высоты всасывания описывается формулами (2.8) и (2.11), уравнение (2.107) преобразуется следующим образом:
Ж + (2.108)
В зоне полного насыщения f ^ 0 и дг2
П ко
При этом 1] =
ТАБЛИЦА 24
Соотношения между переменными уравнений (2.106) и (2.109)
Є
|
T |
|
"Ф е F |
|
Р |
ГЬ—----- In 6
|
Е |
|
Р* |
|
Рг 2 |
|
/7 = Т]Є |
А
Р г
1 , kQ. г
<Ц^е » J
2
R\=Fe
* Здесь значение принимается положительным.
Задание конвективного члена осуществляется током, пропорциональным градиенту переменной ті, определенной на предыдущий момент времени. Дальнейшее упрощение схемы решения уравнения можно провести введением еще одной новой переменной F (табл. 24)
Li
Р = rje 2 .
|
У-о о |
Последнее позволяет представить уравнение (2.108) в виде 4. р2 F-r(F\ дР
(2.109)
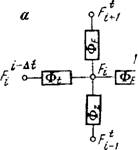
Схема решения этого уравнения показана на рис. 29, а. Как видно, в данном случае задание истока осуществляется просто в зависимости от потенциала F.
|
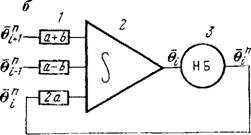
Рис. 29. Схема моделирования уравнения влагопереноса на сетке сопротивлений (а) и на АВМ (б) уравнения (2.118). |
Токовое сопротивление определяется по формуле Фл?
Р2Л 2
Уравнений (2.106) и (2.109).
Табл. 24 позволяет легко переходить от одних переменных к другим.
Решение уравнения (2.58) производится по схеме Либмана с сопротивлениями сетки, равными
Переход от фильтрационных сопротивлений к омическим осуществляется с помощью масштабных коэффициентов. Рассмотрим, как преобразуются граничные условия. На свободной поверхности,
В том случае, если она неподвижна, f — 0, 2 = 0, F = ~
Р
K
На подвижной границе і[з = 0, F — е 2 . Таким образом, задается условие полного насыщения. Граничное условие II рода строится, исходя из зависимости для заданной скорости влагопереноса
Или
В терминах F значение скорости влагопереноса будет иметь вид рг _ Р* \
Е 2 + Р^е 2 J. (2.111)
Рассматривая разность в точках (/+1) и /, это условие можно записать в следующем виде:
|
— V ехр ^ + --------------- |
|
2 |
1
0,5р-----
1-і--------- Р-. (2.112)
Дг Аг
Когда граница непроницаема для потока влаги, в соотношении (2.112) полагаем и = 0, тогда
0,5р
Ft.^-Fi----------------- (2.113)
Соответственно
0,5р 1
Пі+1 = -П/---------- Т~. (2.114)
При наличии испарения и транспирации на поверхности земли необходимо знать зависимость испарения от влажности или всасывающего давления.
В соответствии с закономерностями испарения рассмотренное в § 2 граничное условие при pF>pFfe запишется следующим образом:
E(pF0-pF)=ft(-g.-l). (2.115)
Значение переменной Fi+i находится из соотношения
0,5р —І-- + Л2
Ехр
(2.116)
Для облегчения подбора перед решением задачи на модели целесообразно построить график зависимости Fi+l от F,-. Несмотря на то что рекомендуемые преобразования значительно облегчают расчеты влагопереноса на электроинтеграторе, все же этот процесс остается трудоемким и длительным. В связи с этим перспективным представляется использование моделирующих устройств с функциональными элементами, которые позволяли бы осуществлять автоматическое изменение сопротивлений или емкостей в зависимости от потенциала. В этом отношении интересны предложения А. Б. Ситникова по использованию нелинейных сопротивлений, значение которых определяется величиной потенциала. Наличие таких сопротивлений позволяет значительно расширить диапазон задач, решаемых на сетках сопротивлений, включая также задачи, связанные с фильтрацией в насыщенной и ненасыщенной зонах. При этом уравнение влагопереноса удобнее представлять в терминах напора (2.32).
Наличие переменных сопротивлений дает возможность решать уравнение (2.32) по схеме Либмана, а при нелинейной емкости с (Я) зз р (Я) и на RC сетках.
В некотором отношении указанным выше особенностям удовлетворяют выпускаемые промышленностью аналоговые вычислительные машины с операционными усилителями (АВМ).
В аналоговых вычислительных машинах используются элементы, осуществляющие операции интегрирования, сложения, вычитания, умножения и деления над непрерывными величинами, представленными электрическими напряжениями. Кроме того, в АВМ имеются элементы, воспроизводящие функцию одной из переменных. При постановке задачи на АВМ уравнение (2.32) решается относительно производной.
Поскольку на большинстве АВМ число функциональных блоков и блоков умножения ограничено, решение уравнения (2.32) в полной постановке, по-видимому, нецелесообразно, в связи с этим исходное уравнение выгоднее модифицировать, приведя его к виду (2.34).
Уравнение (2.34) можно решить по схеме дискретное пространство—непрерывное время, заменив пространственные производные конечноразностными аналогами
—У ' + 11 " 2б?) + ~Kz 1 - б?- іЬ Ма^. (2-І 17)
После преобразований уравнение (2.117) представим в виде, удобном для решения на АВМ t
Bi=*j[(a + b)ef+l+(a-b)Bf_l-2aQ»]drt (2.118)
О
А =----------- Ь = - к°
Иоап Дг2 ' 2 Дгцо *
Блок-схема решения этого уравнения показана на рис. 29, б. Как видно из рисунка, в данном случае для решения задачи требуется только один функциональный блок, воспроизводящий функцию у — хп. При моделировании уравнения (2.32) необходимо соблю-
D0
Дать условие Ах<—т~, а при моделировании уравнения (2.117) —
«о
1
Условие Az<—- -.
An
Следует заметить., что аналоговые машины целесообразно использовать и для решения линеаризованного уравнения влагопереноса, потому что при его решении на сетке активных сопротивлений возникают сложности с подбором и заданием производной <50
—При этом, однако, нет необходимости в использовании не-
OZ
Линейных блоков, так как в уравнении (2.34) принимаем п~ 1.
Для примера рассмотрим моделирование влагопереноса на АВМ для оценки питания при глубоком залегании уровня. Условия, рассмотренные в примере, характерны для Предкавказья, где зона аэрации сложена лёссовидными суглинками большой мощности. Для суглинков характерны следующие параметры: & = 0,0504,
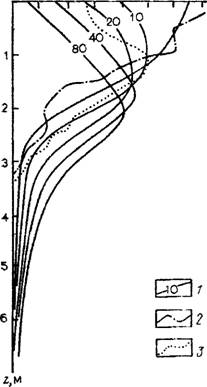
8 = ехр — 0,7г|), 0ТО==О,42, в0 = 0,17. Сначала на модели воспроизводился процесс весеннего увлажнения, длящийся 30 сут. В этот период на поверхности земли задавалась влажность 6 = 0,31, полученная по режимным наблюдениям. Промачивание на конец периода увлажнения достигло 3,4 м (рис. 30), что хорошо согласуется с натурными данными. После периода увлажнения на поверхности земли задавался расход, соответствующий испарению и транспирации в естественных условиях. Эпюры влажности, по-
Лученные на модели, достаточно хорошо согласуются с наблюдаемыми, отражая основные закономерности в миграции влаги.
|
18 20 22 24 26 28 30 32$%
Рис. 30. Результаты моделирования на АВМ процессов промачи - вания и иссушения зоны аэрации. |
При расчетах на ЭЦВМ уравнение (2.32) тоже представляется в конечных разностях. Опыт исследования показывает, что это уравнение лучше решать в терминах напора, поскольку при этом более просто осуществляется сопряжение слоев с различными характеристиками и переход от зоны аэрации к зоне полного насыщения.
|
Щ |
|
ФІ + І, і |
|
Щ |
|
Е = Л zci |
Из анализа методов решения уравнения влагопереноса следует, что для большинства случаев целесообразно использовать неявную схему с итерационным циклом для уточнения значений нелинейных коэффициентов уравнения. При этом значения напора, определяющие приток и отток влаги в блоке, и коэффициенты уравнения должны вычисляться на последующий момент времени
Яі + І
Фі, f -1
I-ht
A t
Распределение влажности по глубине: і — полученное иа модели на различное время, сут; 2 — наблюдаемое через 30 сут после промачиваиия; 3 — то же, через 50 сут
Система нелинейных алгебраических уравнений в данном случае решается методом прогонки в сочетании с методом итераций. Рассматриваемая схема решения является абсолютно устойчивой. Размеры шагов по пространству и времени следует выбирать только из соображений точности аппроксимации дифференциального уравнения конечными разностями. Из устойчивости схемы следует равномерная сходимость к решению дифференциального уравнения, причем порядок точности совпадает с порядком аппроксимации.
Для решения задачи вся зона аэрации разбивается на блоки. При этом зону корнеобитания при решении задач, связанных с прогнозом инфильтрационного питания и большой мощности зоны аэрации целесообразно выделить в один блок. Размеры блоков определяются как мощностью зоны аэрации, так и ее неоднородностью. При разбивке границы блоков должны соответствовать границам слоев с различными водно-физическими характеристи
ками. Слой небольшого размера, особенно если он залегает на глубине подошвы почвенного слоя, может включать только один блок. Для мощности зоны аэрации до 10 м размер блока может быть порядка 0,1т, где т — мощность зоны аэрации. При более глубоком залегании уровня целесообразны блоки с размером 1 м. Шаг по времени задается главным образом исходя из режима увлажнения и расходования влаги на поверхности земли. Особенно удобно принимать его равным одним суткам. Это позволяет использовать при решении задачи среднесуточные параметры, определяющие метеорологические условия. Безусловно, для ряда задач шаг по времени может быть большим или меньшим. Однако в случае его увеличения целесообразно провести предварительное численное экспериментирование, доказывающее возможность счета с большим шагом по времени. Для каждого слоя вводят характеристики, определяющие процесс влагопереноса. Начальные условия определяются исходным влагосодержанием в зоне аэрации и задаются либо исходя из непосредственных наблюдений, либо расчетом.