ГИДРО­ГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ

Метод локальных фильтрационных сопротивлений

Учет сопротивлений локальных зон резкой деформации потока эффективно осуществляется на основе так называемого метода ме­стных (локальных) фильтрационных сопротивлений, идея которого заключается в том, что фильтрационные сопротивления, обуслов­ливаемые локальными деформациями потока, не зависят от общих условий формирования потока и определяются только его строе­нием (геометрическим и фильтрационным) в зоне локальной де­формации. В геофильтрационных расчетах метод локальных со­противлений имеет наибольшее распространение для учета сопро­тивлений горизонтальных дрен, контурных систем скважин, кана­лов, водотоков и водоемов.

Локальное сопротивление несовершенных горизонтальных дрен определяется тем, что вблизи дрены происходит деформация по­тока в вертикальном сечении. Учитывая это сопротивление, можно перейти от несовершенной дрены с напором Яд к эквивалентной совершенной дрене с напором Ял, соответствующим среднему на­пору на линии дрены, причем для их связи используется соотно­шение

Ял — Яд = £Нд, (3.1)

Где величина LHд является параметром, характеризующим вели­чину локального сопротивления придренной области; £Вд зависит от степени несовершенства дренажа и неоднородности строения

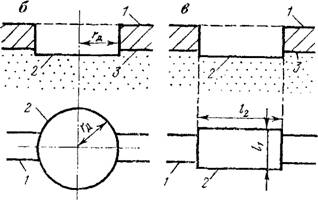
А — в однородном пласте; б — в двухслой' ном пласте; в — канал в покровных отло­жениях

Рис. 36. Несовершенная скважина.

А — в однородном пласте; б — прн наличии глинистого слоя

Водоносных отложений под дреной. Расчетные зависимости для определения в различных условиях приведены в [13, 17]. В ча­стности, для дрены малых размеров в однородном пласте (рис. 35, а)

£нд = 0,73m lg-^r

Где расчетный диаметр дрены dH = 0,56PH, а Рд — смоченный пери­метр дрены; формула (3.1а) справедлива при da < 0,25тд.

Для двухслойного пласта, состоящего из покровного (слабопро­ницаемого) слоя мощностью та с коэффициентом фильтрации ka и нижнего (основного) водоносного слоя мощностью тн с коэффи­циентом фильтрации kH, при расположении дрены в верхнем слое (рис. 35, б) в случае &Н>Ю&П и dH<0,3mn можно считать

(3.1(f)

Для контурных систем скважин, располагаемых с определенным шагом а по прямолинейным или круговым контурам на расстоя­ниях, больших а от границ потока, согласно методу фильтрацион­ных сопротивлений [38], можно заменять линейную батарею пс скважин с дебитом Qc линейным стоком длиной / — пса с суммар­ным расходом Q = ncQc; при этом напоры Ял на линейном стоке оказываются равными среднему напору на линии скважин. Для
контура совершенных скважин связь между напором Ял и напо­ром в скважине Нс имеет вид [38J

Нл — Не= LKc, (3.2)

Где L„c — эквивалентная длина сопротивления контура скважин, определяемая для скважин диаметром dc по формуле

LKC = afKC = 0,366a Ig-j^-. (3-3)

Для учета дополнительного сопротивления за счет гидродина­мического несовершенства скважин к fKC добавляется величина fHC безразмерного сопротивления на несовершенство скважины, кото­рая составляется из величины f° , зависящей от геометрического

Расположения скважины (относительно подошвы и кровли пласта) и неоднородности строения пласта, а также из величины /ф, харак­теризующей сопротивление прискважинной зоны. Величина должна определяться по данным опытно-фильтрационных работ [20, 38], а /о при сравнительно простых строениях водоносных

Пластов может рассчитываться по формулам, получаемым из ана­литических решений фильтрационных задач.

В однородном пласте (рис. 36, а) для скважины, примыкающей к кровле или к подошве (при £7 = 0), величина fRC определяется вы­ражением [20]

F°m = 0,366 (-^Lri - igr - М- _ |g _ 0,035, (3.4)

А для скважины, не примыкающей к кровле или подошве пласта (при с/1>0,1), можно считать

Її - 0,366 pfl igAZl __ig Jpj + Ј, (3.4a)

Где величина e зависит от c=cjm и определяется по следующим данным:

С. . 0,1 0,15 0,2 0,25 0,3 0,4 0,5 є. . 0,36 0,17 0,08 0,03 0 -0,03 -0,035.

Гидродинамическое несовершенство скважины существенно за­висит от неоднородности строения водоносного пласта и потому расчеты величин /°нс по схеме однородного пласта следует рас­сматривать как ориентировочные. Для некоторых схем неоднород­ности пласта имеются аналитические решения для расчетов вели­чины . В частности, для пласта, разделенного глинистым слоем

(рис. 36, б), используя предпосылку перетекания, получим выра­жение [13, 17]

4 = 0,366^1,^. ^д/Ж^Т^у. (3.5)

Б

Рис. 37. Комбинированный дренаж.

А — со скважинами-усилителями, б — с копаными «окнами»; 1 — дно горизонтальной дреиы; 2 — коИтур «окна»; 3 — поверхность земли

Удобным приемом учета этих сопротивлений является замена дей­ствительного (геометрического) радиуса скважины гс на его рас­четное значение г° , связанное с величиной fHC соотношением

R° = г e"2jlfHC 'с ' сс

Связь между уровнями на линии дренажа и в дрене, опреде­ляемая зависимостью (3.1), остается справедливой и для комби­нированного дренажа (рис. 37, а), в котором горизонтальный дре­наж усиливается вертикальными скважинами, расположенными одна от другой по линии дренажа на расстоянии а. При а, мень­шем половины расстояния между дренами, применение метода со­противлений позволяет получить следующее выражение для рас­четной длины зоны резкой деформации комбинированного дренажа

LkcLm

(3.7)

^кс

Где /,Нд определяется по формулам (3.2) — (3.3), a LKC по формуле (3.6).

Расчетный напор комбинированного дренажа Якд при различ­ных уровнях воды в дрене Яд и скважинах Нс определяется по формуле

■^КД . іj LKll

--- Н с - J-----

Нд ^кс

В частном случае, когда самоизлив из скважин осуществляется на уровне воды в дрене (//д = //с), получим Нкк — Нт — Нс-

Аналогичным путем можно построить расчетные зависимости для прерывистого горизонтального дренажа, представленного «ок­нами» различной формы, расположенными на расстоянии сто друг от друга (рис. 37, б). Прежде всего приведем решение для усло­вий, когда такой дренаж работает только «окнами». В этом случае расчетная длина Ьпя, характеризующая сопротивление на несовер-

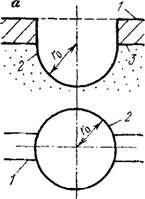
Рис, 38. Типичные геометрические формы фильтрующего «окна» (в разрезе и в плане).

А —■ полусферическая, б — плоская круглая, в — щелевидная; I — дно и стеики горизонталь­ной дрены; 2 — коитур фильтрующего «окиа>; 3 — подошва слабопроиицаемых покровных отложений

Шенство прерывистого дренажа, в соответствии с решениями, при­веденными в работе [23J, определяется по формуле

Где го—расчетный радиус «окна», зависящий от его размеров и формы. Для полусферического «окна» (рис. 38, а) го равен гео­метрическому радиусу; для плоского круглого в плайе «окна» ра­диусом гд (рис. 38, б) имеем: го — 0,64гд; для плоских щелевидных «окон» (рис. 38, в) Г0 = &(/|-Н2), где а определяется по следую­щим данным:

H/h. ... О 0,2 0,5 1,0 а 0,25 0,28 0,293 0,295

Этими зависимостями можно пользоваться при cr0 ^ tn и т> >2г0, а при 0,5m<cr<m следует применять формулу

При необходимости учета притока не только через «окна», но и по всей длине дрены дренаж должен рассчитываться как ком­бинированный

— расчетная длина Lкд для такого дренажа опреде­ляется по формуле (3.7), в которой Lkv. заменяется на опреде­ляемую из (3.8), a LHa берется для горизонтальной дрены без учета «окон».

Таким образом, метод локальных сопротивлений позволяет за­менить контурные системы скважин и несовершенных горизон­тальных дрен сплошными совершенными траншеями (галереями), причем напор в такой эквивалентной траншее соответствует сред­
нему напору Ял по линии контурной системы, связанному с напо­ром в скважинах Яс формулой (3.4) или с напором в горизонталь­ной дрене Яд формулой (3.1). Эти формулы можно записать в сле­дующем обобщенном виде:

//д = -2*_£д> (3.9)

Где Яд — напор, задаваемый на дрене; qд — удельный приток к дрене; — эквивалентная длина локального сопротивления дре­нажа; для скважин ЯД = ЯС, qA — QcM /,д = /_кс, для горизон­тальной несовершенной дрены £д = 1нд; для комбинированного дренажа La = LKR и Яд = Якд.

Метод локальных сопротивлений используется также для учета гидродинамического несовершенства ложа водоема или водотока (водохранилища, реки, каналы и т. п.) при подпертом режиме фильтрации, т. е. при наличии гидравлической связи между по­верхностным и подземным потоком [17, 25]. В этом случае поток в берегах водоема (водотока) связывается с водоемом симметрич­ной системой сопротивлений, соединяемых по схемам «треуголь­ника» или «звезды». Величины этих сопротивлений при простом строении ложа водоема имеют аналитические выражения, а в об­щем случае они должны находиться по данным режимных наблю­дений.

На гидродинамическое несовершенство каналов (водотоков) малой ширины существенное влияние может оказывать положение свободной поверхности, так что при этом сопротивление на несо­вершенство канала будет зависеть от расхода потока. Для харак­терного случая канала в слабопроницаемых покровных отложе­ниях, подстилаемых значительно более проницаемым водоносным пластом (см. рис. 35, в), зависимость фильтрационного расхода канала от напора в водоносном пласте может быть получена пу­тем анализа гидромеханического решения задачи фильтрации из канала с нулевой глубиной воды и областью бесконечной прони­цаемости на глубине тп [4, 26]. В этом случае можно пользоваться следующими асимптотическими выражениями, связывающими между собой приведенный удельный фильтрационный расход q — — qlk с разницей напоров АЯ = ЯК—Я в канале и в пласте

Q N+ 0,88 (тп — АН) „ ^ 1Л4

Д7Г =------------ к---------- " "РИ N>mn (ЗЛ0)

И

_ АЯ

Q = м _ JL (тп-АН) е * при N<mn. (3.10а)

Числовые значения безразмерных фильтрационных сопротивле­ний такого канала Ф — AH/q приведены в табл. 33.

Из этих данных можно видеть, что наибольшая зависимость

Сопротивления Ф от расхода (или разницы напоров А Я) харак-

Терна для условий фильтрации из канала (водотока), что имеет важное значение при учете фильтрационных потерь из каналов и водотоков. При больших значениях АЯ удельный расход фильт­рационных потерь водотока стремится к своему максимальному значению q = N, соответствующему условиям свободной фильт­рации.

Понижение уровня в водоносном пласте АЯсв, начиная с ко­торого фильтрацию из водотока можно считать свободной, при N> >та находится из уравнения (3.11), если задать в нем АН = = АЯСВ и q~( 1 — бq)N, где бq — допустимая погрешность расче­тов расхода. Решая полученное выражение относительно АЯсв. получаем

ДЯсв = —- = 0,57¥ + 0,5 - "V тп

W=N/mn. (3.11)

При N<mn зависимость q от А Я не выражается в явном виде, так что в этом случае величину АЯсв приходится искать численным путем. При mn<jV<0,02mn величина АЯсв хорошо аппроксими­руется выражением

АНсв = тя (аі - a2lg-^j, (3.11а)

Где параметры а% и а2 зависят от погрешности 8д, причем а\ — = 0,88, а2 — 0,84 при 6g = 0,l; at — 0,64, а2 = 0,7 при бв = 0,2 и йі = 0,4, а2 — 0,5 при бд == 0,4.