ГИДРОГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ
Инфильтрационное питание
Характерными для орошаемых территорий являются условия задания распределенного инфильтрацнонного питания (особенно при поливах и промывках).
Для непосредственной реализации заданного инфильтрацнонного (площадного) питания на электрических моделях требуется задать площадное распределение тока соответствующей интенсивности. На сеточной модели этот ток подается в узловые точки, а на сплошной модели распределяется по дискретной сетке [17].
При моделировании крупных систем орошаемые поля в плане представляют собой площадные источники инфильтрации, имеющие, вообще говоря, многоугольную форму. Для удобства расчетов можно составлять эти площади из отдельных прямоугольных участков. Тогда моделирование инфильтрации с орошаемых полей сводится к реализации на моделях системы прямоугольных площадок с заданным инфильтрационным питанием. При неизменном питании (начиная со времени t= 0) подпор АН под действием такой площадки, согласно (3.14), представляется выражением
Где Qw — расход инфильтрации на площадке; f пл — единичная функция площадки инфильтрации. Для определения на модели величины /пл удобно использовать расчетный прием, основанный на том, что влияние формы источника-стока заметно проявляется только в непосредственной близости от него. Поэтому можно считать, что влияние границ потока для площадного источника, как правило, будет таким же, как и для точечного источника (скважины), расположенного в его центре. Тогда единичная функция прямоугольной площадки инфильтрации представляется выражением
/пл = /°пл-/*> (3-37)
Где /°дл—единичная функция для площадки в неограниченном однородном пласте, определяемая выражением (3.15); fR — дополнительная единичная функция, учитывающая влияние границ потока; при этом величина fR определяется на модели так же, как для точечного источника-стока (скважины) при расположении электрода в центре площадки инфильтрации.
Аналогичным путем решается задача моделирования линейного источника-стока с расходом Q, для которого изменение напора определяется выражением (3.18) при
/л = /л-//г. (3-37а)
Где f°4 — единичная функция для линейного источника-стока в неограниченном однородном пласте, определяемая выражением (3.24); fR — дополнительная единичная функция, определяемая на модели, как для точечного источника-стока (скважины), располагаемого в середине линии.
Используя такой прием расчета единичных функций, следует на модели найти значения единичной функции скважины /с, устанавливаемой в середине площадки или линии, и рассчитать по этим значениям величины fR — fc — f° , находя из (3.13).
После этого расчеты функций /Пл и /л ведутся по выражениям (3.37) и (3.37а). Этот же расчетный прием может эффективно использоваться и для модельных расчетов площадных и линейных систем скважин, которые на основе метода локальных сопротивлений могут заменяться площадными и линейными стоками. При этом должны учитываться дополнительные понижения уровня в скважинах А5С по отношению к уровню на распределенном (площадном или линейном) стоке, которые определяются для площадной системы по формуле (3.17), а для линейного ряда по формуле (3.2), поскольку А5С = НЛ — Нс.
При моделировании орошаемых полей (площадей инфильтрации) на сеточной модели в блоках, располагаемых по краям полей, площадь инфильтрации лишь частично занимает площадь блока. В узловой точке такого блока задается расход инфильтрационного питания, поступающего в пределах блока. Учет реальной конфигурации поля в пределах блока можно осуществить, добавляя напор А Я, представляющий собой разницу напоров от действия реального участка поля и площадки инфильтрации того же расхода, «размазанной» по площади блока. Из-за локальности влияния этой поправки ее можно вводить без учета границ потока, считая
Где rj, —определяемые по формуле (3.16) или с помощью табл. 34 расчетные расстояния от расчетной точки до реального участка поля и до участка, занимающего площадь блока.
При задании на всей моделируемой территории одинаковой интенсивности инфильтрации удобные решения можно получить, вводя преобразования в расчетную функцию (напор), позволяющие исключить непосредственное моделирование w. При моделировании стационарных задач в качестве расчетной можно рассматривать функцию
Tfw = tf+(w-w0) ~r+ (w + w0) -&rr + - f #o> (3.39)
|
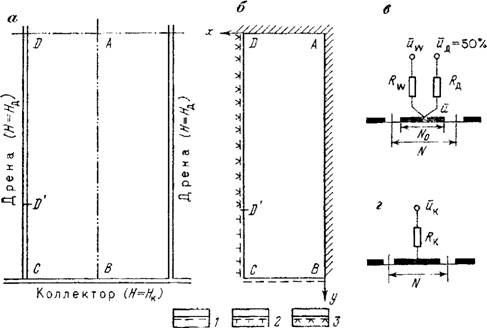
Рис. 45. Построение модели планового потока с учетом ннфильтрационного питания путем введения вспомогательной функции Я0. |
А — область фильтрации; б — схема электрической модели; в — подсоедииеиие сопротивлений на контуре дрены, г — подсоединение сопротивления на контуре коллектора; / — контур коллектора; 2 — коитур неработающей дрены. 3 — контур работающей дрены
Где w0, q и Но — любые постоянные величины, которые задаются из условия получения наиболее удобных для моделирования граничных условий.
При моделировании нестационарной фильтрации можно также использовать вместо напора Н расчетную функцию t
//w == Я — I — dt, (3.40)
О **
Причем в случае w = const
#w = tf_JL*. (3.40а)
Задаваемая таким образом функция Нw уже не будет зависеть от инфильтрации и моделируется без ее учета, но с соответственно измененными граничными условиями.
В качестве примера применения такого преобразования приведем построение модели для потока между систематическими дренами с учетом действия глубоких коллекторов (рис. 45, а) при равномерном стационарном инфильтрационном питании во всей области потока. Вследствие симметрии потока между противоположными коллекторами и дренами можно изолированно рассматривать область ABCD, считая линии АВ и AD непроницаемыми
границами. На линии коллектора (СВ) задается граница третьего рода
|
(3.41) |
ДН Н - Нк
Ду 2 LK
Где Як— уровень воды в коллекторе; LK —LHд — параметр сопротивления на несовершенство коллектора. На линии дрены в пределах ее работающей части (DD') также задается условие третьего рода
Где Яд — уровень воды в дрене; Ья — параметр сопротивления на несовершенство дрены. В пределах неработающей части, где Я< <ЯД, линия CD является непроницаемой границей, причем точка D' заранее неизвестна и должна определяться из условия Я = ЯД.
Для построения модели введем вспомогательную функцию Я0, связанную с напором Я соотношением
Т = Н + -~. (3.42)
Эта функция описывается уравнением Лапласа на плоскости х, у, а ее граничные условия имеют следующую форму: на линиях АВ и AD сохраняется условие непроницаемой границы (дН°/ду = О на линии AD и дН°/дх~0 на линии АВ), на линии ВС должно выполняться условие III рода
Дно Н°~Н°К. WJC2
~ 2Ьк "!!«"■+-lb (3-43)
W L
На линии CD' будет условие второго рода дН°/дх — --—, а на
Линии DD' условие третьего рода
№ — н°
W L " ПЛ rr0 ri wЈ2
Причем точка D находится из условия Я0 = Я° . Эту задачу удобно решать на сплошной электрической модели с удельным сопротивлением рм при относительном потенциале ЇЇ = ~Х
Х(Я° — НК)/(Н° — Нк). Такая модель по линиям АВ и AD обрезается, по линиям ВС и CD подключаются сопротивления, как это показано на рис. 45, в, г, причем
RK = Рм-^дгк-; R. i = Рм ик = —^ ^у' (3-44)
Где N—ширина натурного потока, относящегося к одному сопротивлению. Сопротивления Rw служат для подачи тока /w, соответ
ствующего расходу потока wLN\ величина этого сопротивления определяется соотношением
|
|
(3.44а)
Где потери относительного потенциала A{7W = ?7W — U должны задаваться в пределах до 50 %. На линии CD сопротивление /?д отсутствует.
При выполнении моделирования должно быть предварительно подбором установлено положение точки D из условия U = 11ж, после чего сняты значения потенциалов в расчетных точках, по которым находятся величины напоров из выражения
|
|
|
2 Т • |
|
W*2 |
|
(3.45) |
Я = Як + 2(Яд +