Геометрическая оптика

Интерференция световых волн TC «Интерференция световых волн» f D l «1&quot

Когерентность Временная и пространственная когерентность. Способы наблюдения интерференции света. Классические интерференционные опыты: бипризма Френеля, бизеркала Френеля, опыт Юнга, интерференция в тонких пленках, кольца Ньютона. Интерферометры. Многолучевая интерференция. Просветленная оптика и другие практические применения интерференции.

Интерференция световых волн. Когерентность волн.

Интерференцией света называется наложение двух или более волн, при котором происходит пространственное перераспределение интенсивности света, наблюдаемое в виде темных и светлых полос.

Возникновение интерференции связано, во-первых, с тем, что для векторов напряженности электрических полей, описывающих электромагнитные волны, выполняется принцип суперпозиции. Так при наложении двух волн, каждая из которых создает в точке наблюдения соответственно электрические поля напряженностью E1 и E2, результирующая напряженность в точке наложения будет равна: Ep = E1 + E2 (1)

Возникновение интерференции связано с тем, что все регистрирующие приборы, в том числе и человеческий глаз, регистрируют не величину напряженности электрического поля, а величину усредненного по времени потока энергии волны, которая характеризуется интенсивностью света (I), равной квадрату амплитуды напряженности электрического поля волны E0: I = E02 (2)

При наложении нескольких волн интерференция наблюдается далеко не в каждом случае. Термин когерентность волн характеризует способность волн при наложении интерферировать. Волны называются когерентными, если при их наложении возникает интерференционная картина и некогерентными, если при их наложении интенсивности волн суммируются и интерференционная картина не возникает. Волны когерентны, если разность фаз между ними остается постоянной во время наблюдения. Для некогерентных волн разность фаз между ними хаотически изменяется во времени.

Если колебания возбуждаемые волной в достаточно близких точках псевдоволновой поверхности оказываются когерентными, то такая когерентность называется пространственной.

Фаза колебания при переходе от одной точки псевдоволновой поверхности к другой изменяется беспорядочным образом. Зведем расстояние рког, при смещении на которое вдоль псевдоволновой поверхности случайное изменение фазы достигает значения ~л. Колебания в двух точках псевдоволновой поверхности, отстоящих друг от друга на расстояние, меньшее рког, будут при-элизительно когерентными. Расстояние ркОГ называется длиной тространственной когерентности или радиусом когерентности. Из (120.13) следует, что ρ=λφ (120.14)

Схема двухлучевой интерференции(1)

Рассмотрим наложение двух световых волн, идущих от двух источников S1 и S2, в точку Р (см. рис.1). Волны будем полагать монохроматическими и плоскими. Тогда выражения для напряженностей электрического поля двух волн можно записать в виде: E1 = E10 cos(ωt – kz), E2 = E20cos(ω1t – k1z1) (3)

Где Е10 и Е20 - амплитуды первой и второй волн, ω и ω1 - циклические частоты первой и второй волн, k и k1 - волновые числа первой и второй волн (k = 2π/λ,здесь λ - длина волны), z и z1 - расстояния пройденные волнами от источников до точки наблюдения, t - время в момент наложения волн.

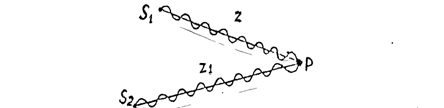Рис.1- Схема двухлучевой интерференции.

Обозначив фазы двух волн, т. е. аргументы периодической функции (в данном случае косинуса), описывающей волны, через φ и φ1 соответственно, можно записать, что разность фаз двух волн равна: ∆φ = φ – φ1 = (ω – ω1)t – kz – k1 z1 . (4)

Из этого выражения видно, что условие когерентности, т. е. постоянство разности фаз во времени, может выполняться лишь для волн с одинаковыми частотами (ω = ω1).

Циклическая частота однозначно связана с волновым числом k = ω/v , (где v - фазовая скорость света в среде - величина для когерентных волн разность фаз определяется геометрической разностью хода волн от источников до точки наложения волн (∆):

∆φ = k (z – z1) = k ∆ . (5)

Волновое число в среде (kc) пропорционально показателю преломления среды: kc = k n, (6)где k - волновое число в вакууме.

Оптическую разность хода (∆), т. е. разность оптических длин путей двух волн ( L 01 и L02 ): ∆φ = k (Lo1- Lo2 ) = k ∆ (7)

Оптическая длина пути волны, прошедшей несколько различных сред (см. рис.2), находится как сумма произведений показателя преломления среды (n 1) на геометрическое расстояние, пройденное волной в данной среде (z1): L0 = n1 z1 + n2 z2 + ... + n1 z1 +... (8)

Оптической длиной пути световой волны называется произведение геометрической длины пути (z1) световой волны в среде на абсолютный показатель преломления (n1) данной среды: Loпт = zi · ni

Зеркала Френеля.

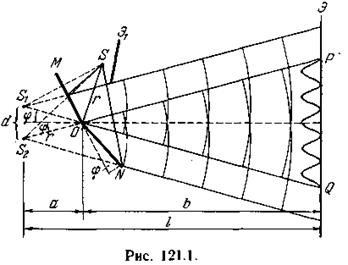Два плоских соприкасающихся зеркала ОМ и ON располагаются так, что их отражающие поверхности образуют угол, близкий к л (рис. 121.1). Соответственно угол ф на рисунке очень мал. Параллельно линии пересечения зеркал О на расстоя­нии г от нее помещается прямолинейный источник света S (напри­мер, узкая светящаяся щель). Зеркала отбрасывают на экран Э две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников Si и Si. Непро­зрачный экран Э преграждает свету путь от источника S к эк­рану Э.

Луч OQ представляет собой отражение луча SO от зеркала ОМ, луч ОР — отражение луча SO от зеркала ON. Легко сообразить, что угол между лучами ОР и OQ равен 2ф. Поскольку S и Si распо­ложены относительно ОМ симметрично, длина отрезка OSi равна OS, т. е. г. Аналогичные рассуждения приводят к тому же резуль­тату для отрезка OS2. Таким образом, расстояние между источни­ками Si и S2 равно

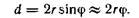
Из рис. 121.1 видно, что 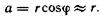Следовательно, 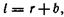где ь — расстояние от линии пересечения зеркал О до Ширина интерференционной полосы:

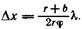(121.1)

Максимальное число интерференционных полос, которое можно наблюдать с по­мощью зеркал Френеля при данных параметрах схемы:

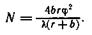(121.2)

20.10).